如何对多个变量的依赖关系进行建模?
- 利用图模型: 存在关系的变量之间用边连接.
- 利用潜变量: 假设多个变量是从同样的”诱因”产生.
本文内容来自 Machine Learning: A Probabilistic Perspective 的第 11 章 Mixture models and the EM algorithm1. 原书错误修订2.
1. 潜变量模型
上面第2点的”诱因”就是我们说的潜变量 (latent variable), 潜变量是不能直接观测到的, 包含潜变量的模型称为潜变量模型 (latent variable models, LVM). LVM 相比于图模型有以下优缺点:
- 优点: 通常来说参数更少
- 缺点: 拟合起来更困难 (因为包含不可观测的变量)
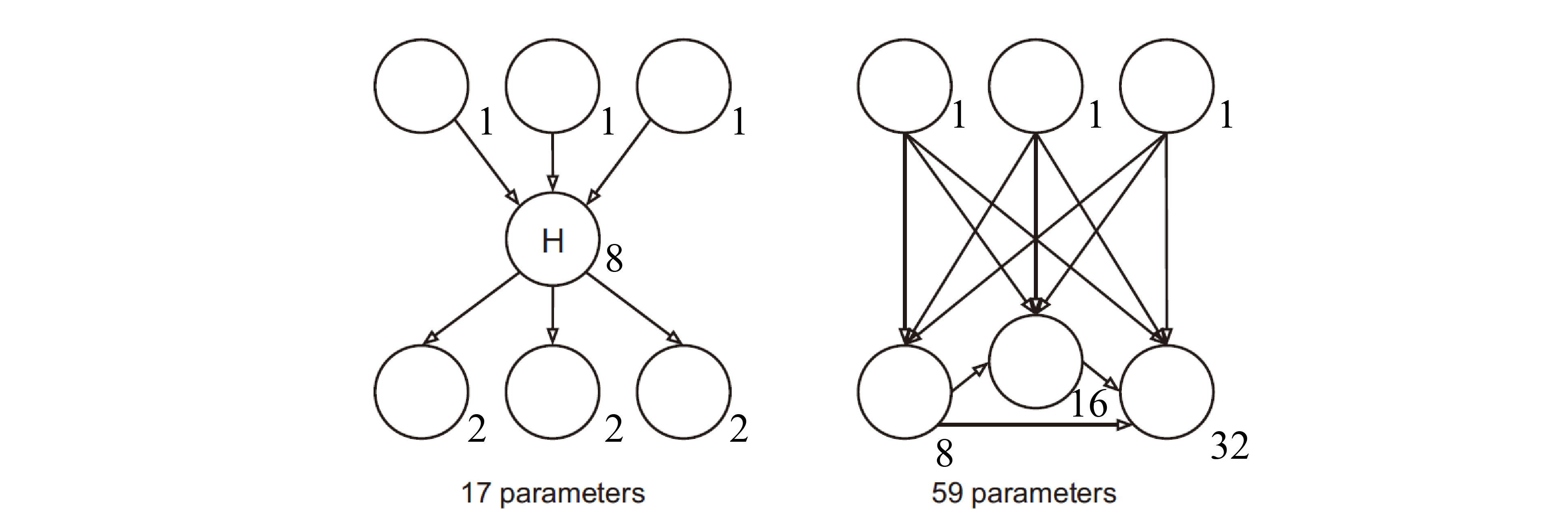
图 1. 潜变量模型和图模型的参数量对比
如上图所示, 假设所有节点都是二值的, 那么左侧的模型有 17 个自由参数, 右侧的模型有 59 个自由参数. 计算参数数量的方式如下: 1) 当前变量为二值变量, 所以根据归一化原则只需要一个自由参数 \(2 - 1=1\); 2) 当前变量存在条件变量时, 相应的自由参数数量随条件变量的数量呈指数增长 \(2^n\). 比如上图左侧中间的 H 节点, 有三个条件变量 (入度), 那么其自由参数的数量为 \((2 - 1)\times 2^3=8\) 个.
利用潜变量, 我么可以得到丰富的 LVM, 如下图所示, 有 (a) 多对多模型, (b) 一对多模型, (c) 多对一模型 和 (d) 一对一模型.
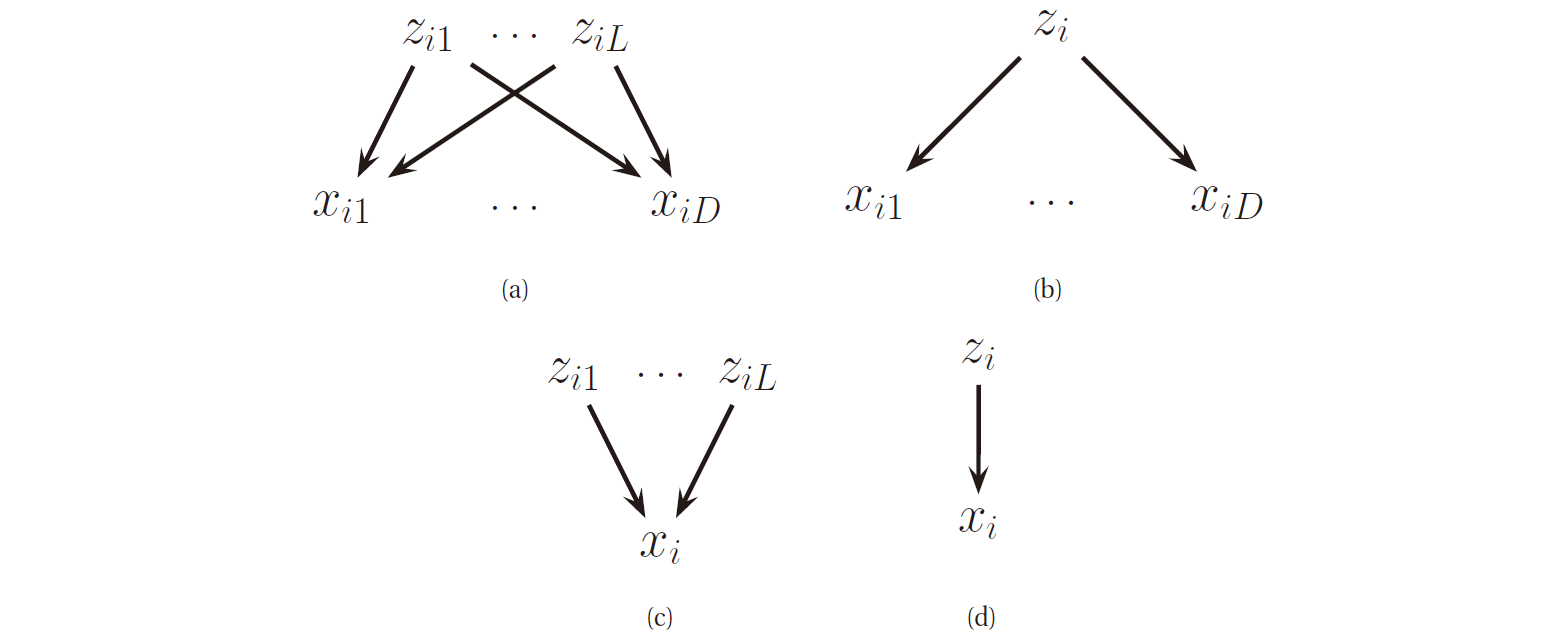
图 2. 潜变量模型表示为 DGM
2. 混合模型
\(\newcommand{\cat}{\text{Cat}} \newcommand{\x}{\mathbf{x}} \newcommand{\tb}{\boldsymbol{\theta}} \newcommand{\mub}{\boldsymbol{\mu}} \newcommand{\Sigmab}{\boldsymbol{\Sigma}}\) LVM 最简单的形式就是当 \(z_i\in\{1,\dots,K\}\) 表示一个离散潜变量, 我们通常使用一个离散先验 \(p(z_i)=\cat(\pi)\) . 对于似然, 我们用条件分布来表示 \(p(\x_i\vert z_i=k)=p_k(\x_i)\) , 其中 \(p_k\) 是第 k 个观测变量的基分布 (base distribution) , 可以是任何分布类型. 潜变量和观测变量合并起来就得到了混合模型 (mixture model) , 因为我们混合了 K 个基分布:
\[p(\x_i\vert\tb)=\sum_{k=1}^K\pi_kp_k(\x_i\vert\tb)\]因为我们采用了加权平均的方式, 且混合权重 \(\pi_k\) 满足 \(0\leq\pi_k\leq1\) , 并且 \(\sum_{k=1}^K\pi_k=1\) , 所以这是 \(p_k\) 的凸组合.
2.1 高斯混合模型
混合模型中使用最为广泛的就是高斯混合模型 (mixture of Gaussians, MOG or Gaussian mixture model, GMM) . 在 GMM 中, 每个基分布都是均值为 \(\mub_k\) 协方差矩阵为 \(\Sigmab_k\) 的多元高斯分布, 因此 GMM 的形式为:
\[p(\x_i\vert\tb)=\sum_{k=1}^K\mathcal{N}(\x_i\vert\mub_k,\Sigmab_k)\]下图是包含 3 个分量的 GMM 的例子.
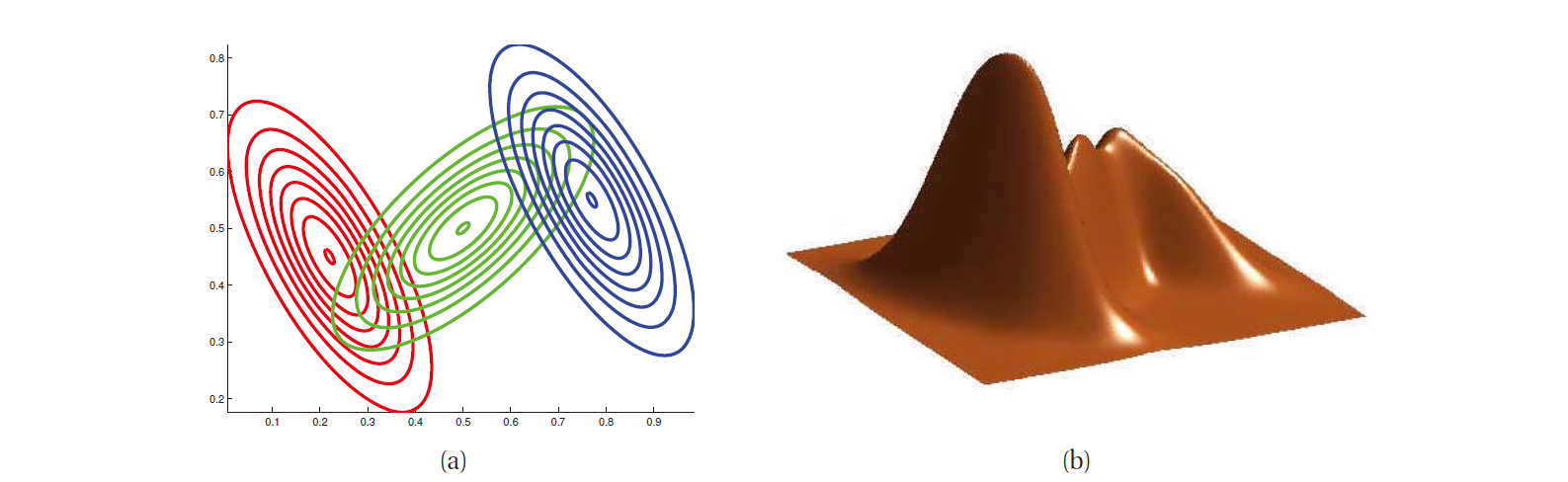
图 3. 3 个高斯分布的混合模型
在高斯分布的数量足够大的情况下, GMM 可以用来近似 \(\mathbb{R}^D\) 中的任意密度分布.
2.2 Multinoullis 混合模型
假设我们的数据是是由 \(D\) 维的比特向量组成, 那么类条件密度为:
\[p(\x_i\vert z_i=k,\tb)=\prod_{j=1}^D\text{Ber}(x_{ij}\vert\mu_{ij})=\prod_{j=1}^D\mu_{jk}^{x_{ij}}(1-\mu_{jk})^{1-x_{ij}}\]其中 \(\mu_{jk}\) 是第 \(k\) 类中第 \(j\) 个比特为开的状态(反之为闭)的概率.
引入潜变量后, 潜变量并没有实际含义, 只是用来使得模型更强. 可以证明该混合模型的均值和协方差为:
\[\begin{align} \mathbb{E}[\x] &=\sum_k\pi_k\mub_k \\ \text{cov}[\x] &=\sum_k\pi_k[\Sigmab_k+\mub_k\mub_k^T]-\mathbb{E}[\x]\mathbb{E}[\x]^T \end{align}\]其中 \(\Sigmab_k=\text{diag}(\mu_{jk}(1-\mu_{jk}))\) . 所以尽管每个成分的分布是可分解的, 但联合分布是不可分解的. 因此混合分布可以建模变量间的关系, 而简单的 Bernoullis 分布的乘积却不能.
2.3 使用混合模型聚类
混合模型主要有两种应用:
- 当作黑盒密度模型 \(p(\x_i)\) , 可以用于数据压缩, 离群值检测, 生成式分类器
- 用于聚类
聚类的方法是, 首先拟合混合模型, 然后计算后验概率 \(p(z_i=k\vert\x_i,\tb)\) , 它表示数据点 \(\x_i\) 属于第 \(k\) 个类别的概率, 或称为责任 (responsibility) , 通过贝叶斯公式计算如下:
\[r_{ik}\triangleq p(z_i=k\vert\x_i,\tb)=\frac{p(z_i=k\vert\tb)p(\x_i\vert z_i=k,\tb)}{\sum_{k'=1}^Kp(z_i=k'\vert\tb)p(\x_i\vert z_i=k',\tb)}\]这个方法称为软聚类 (soft clustering) , 这个计算过程和生成式分类器相同. 软聚类和生成式分类器的区别在于训练过程: 前者无法观测 \(z_i\) 的值, 而生成式分类器观测了 \(y_i\) 的值 (扮演了 \(z_i\) 的角色).
我们可以通过 \(1-\max_k r_{ik}\) 来表示聚类的不确定性程度. 假设该值很小, 那么我们就可以使用最大后验 (maximum a posterior, MAP) 计算硬聚类 (hard clustering) , 为:
\[z_i^*=\underset{k}{\arg\max}~r_{ik}=\underset{k}{\arg\max}[\log p(\x_i\vert z_i=k,\tb)+\log p(z_i=k\vert\tb)]\]这里给出二值数据聚类的一个例子, MNIST 手写数字数据集, 我们忽略类别标签, 拟合一个 Multinoullis 的混合模型, 使用 \(K=10\) , 并可视化出聚类中心 \(\hat{\mub_k}\) , 如下图所示.

图 4. MNIST 混合模型聚类中心
注意这 10 个聚类中心和数字的 10 个类别标签并不一致, 这是因为模型潜在的变量不止 10 个, 比如数字 7 就可以有带把和不带把两种写法, 因此如果要区分开 10 个数字类别, 就需要大于 10 个的聚类数. 这告诉我们, 聚类的结果不一定是可靠的, 在实际应用中需要小心斟酌.
3. EM 算法
对于大多数机器学习和统计学习模型来说, 如果我们可以观测到所有随机变量的值, 那么在使用 MLE 或 MAP 进行参数估计时是非常容易的. 但是, 如果存在缺失数据或潜变量时, 就很难计算 MLE 或 MAP 了.
一种办法是利用基于梯度的优化器寻找负对数似然 (negative log likelihook, NLL) 的局部极小值:
\[\text{NLL}(\tb)\triangleq-\frac1N\log p(\mathcal{D}\vert\tb)\]然而, 潜变量模型往往存在一些约束, 如协方差矩阵要是正定的, 混合权重的和为 1 等, 在梯度优化时比较麻烦. 因此, 这里引入期望最大化 (expectation maximization, EM) 算法. 这是一种简单的迭代算法, 每一步可以求闭式解, 同时该算法自动保证了约束成立.
EM 算法的思路是: 如果数据完整的观测到了, 那么我们就可以采用 MLE/MAP 估计. 因此 EM 算法分为两步:
- 给定参数推断缺失的数据 (E-step)
- 给定填充好的数据优化参数 (M-step)
3.1 基本思想
令 \(\x_i\) 是第 i 个观测变量, \(z_i\) 是隐藏变量, 我们的目的是最大化观测数据的对数似然:
\[l(\tb)=\sum_{i=1}^N\log p(\x_i\vert\tb)=\sum_{i=1}^N\log\left[\sum_{z_i}p(\x_i,z_i\vert\tb)\right]\]但是因为 \(\log\) 不能移到求和符号内部, 因此上式难以优化. EM 算法按如下方式解决问题. 定义完全数据的对数似然为:
\[l_c(\tb)\triangleq\sum_{i=1}^N\log p(\x_i,z_i\vert\tb)\]因为 \(\z_i\) 未知, 所以上式无法计算, 所以我们再定义一个期望完全数据的对数似然为:
\[Q(\tb,\tb^{t-1})=\mathbb{E}[l_c(\tb)\vert\mathcal{D},\tb^{t-1}]\]其中 \(t\) 是当前迭代的步数, \(Q\) 是辅助函数. 期望是对上一步的参数 \(\tb^{t-1}\) 和观测数据 \(\mathcal{D}\) 取的. E-step 的目的是计算 \(Q(\tb,\tb^{t-1})\) 或 \(Q\) 中 MLE 依赖的项, 而 M-step 是关于 \(\tb\) 优化 \(Q\) :
\[\tb^t=\underset{\tb}{\arg\max}~Q(\tb,\tb^{t-1})\]如果是计算 MAP 估计, 上式修改为:
\[\tb^t=\underset{\tb}{\arg\max}~Q(\tb,\tb^{t-1}) + \log p(\tb)\]3.2 GMMs 的 EM 算法
本小节介绍如何使用 EM 算法拟合 GMMs. 我们假设高斯混合模型的成分数量 \(K\) 是已知的 (实际中可以作为超参数).
3.2.1 辅助函数
期望完全数据的对数似然为:
\[\begin{align} Q(\tb,\tb^{t-1}) &\triangleq \mathbb{E}\left[\sum_i\log p(\x_i,z_i\vert\tb)\right] \\ &= \sum_i\mathbb{E}\left[\log\left[\prod_{k=1}^K(\pi_k p(\x_i\vert\tb_k))^{\mathbb{I}(z_i=k)}\right]\right] \\ &= \sum_i\sum_k\mathbb{E}[\mathbb{I}(z_i=k)]\log[\pi_k p(\x_i\vert\tb_k)] \\ &= \sum_i\sum_k r_{ik}\log\pi_k + \sum_i\sum_k r_{ik}\log p(\x_i\vert\tb_k) \end{align}\]其中 \(r_{ik}\triangleq p(z_i=k\vert\x_i,\tb^{t-1})\) 是 k 个聚类对于第 i 个样本的责任 (参看本文第 2.3 节).
3.2.2 E-step
E-stem 用来计算 \(r_{ik}\) (因为 MLE 依赖于它, 见 3.1 节):
\[r_{ik}=\frac{\pi_k p(\x_i\vert\tb_k^{t-1})}{\sum_{k'}\pi_{k'} p(\x_i\vert\tb_{k'}^{t-1})}\]3.2.3 M-step
在 M-stem 中, 我们关于 \(\boldsymbol{\pi}\) 和 \(\tb_k\) 优化 \(Q\) . 对于 \(\boldsymbol{\pi}\) , 我们有:
\[\pi_k=\frac1N\sum_i r_{ik} =\frac{r_k}{N}\]其中 \(r_k=\sum_i r_{ik}\) 是属于第 \(k\) 类的点的加权数量. 对于 \(\tb_k\) , 即高斯分布的 \(\mub_k\) 和 \(\Sigmab_k\) , 从 \(Q\) 中最后结果的第二项我们有:
\[\begin{align} l(\mub_k,\Sigmab_k) &= \sum_k\sum_i r_{ik}\log p(\x_i\vert\tb_k) \\ &= -\frac12\sum_i r_{ik}[\log\vert\Sigmab_k\vert + (\x_i-\mub_k)^T\Sigmab_k^{-1}(\x_i-\mub_k)] \end{align}\]上式其实就是计算多元高斯分布 (multivariate Gaussian, MVN) 的 MLE. 可以证明新的参数估计为:
\[\begin{align} \mub_k &= \frac{\sum_i r_{ik}\x_i}{r_k} \\ \Sigmab_k &= \frac{\sum_i r_{ik}(\x_i-\mub_k)(\x_i-\mub_k)^T}{r_k}=\frac{\sum_i r_{ik}\x_i\x_i^T}{r_k}-\mub_k\mub_k^T \end{align}\]上面的式子是直观的: 聚类 \(k\) 的中心就是所有赋以第 \(k\) 类的样本点加权平均, 协方差矩阵正比于加权的经验散布矩阵 (scatter matrix) . 上面两式的求法类似于 MVN 的 MLE 求法, 后者在原书中1 的第 4 章 4.1.3.1 节给出了详细的证明过程.
3.2.4 K-means 算法
K-means 聚类算法可以看作 GMMs 的 EM 算法的一个特例. 考虑上述 GMM 增加两个假设:
- \(\Sigmab_k=\sigma^2\mathbf{I}_D\) 对于所有类别 \(k\) 是固定的
- \(\pi_k=1/K\) 也是固定的
因此只有聚类中心 \(\mub_k\) 是需要估计的. 考虑使用如下的 \(delta\) 函数近似 E-step 中的后验计算:
\[p(z_i=k\vert\x_i,\tb)\approx\mathbb{I}(k=z_i^*)\]其中 \(z_i^*=\arg\max_k p(z_i=k\vert\x_i,\tb)\) , 这称为硬 EM (hard EM), 因为我们没有采取加权而是直接赋值的形式来指定数据点的类别. 因为我们假设每个聚类的协方差矩阵都是相等的单位阵, 所以 \(\x_i\) 最可能被分到的聚类可以用最近的原型来表示:
\[z_i^*=\underset{k}{\arg\min}\Vert\x_i-\mub_k\Vert_2^2\]因此在 E-step, 我们在 \(N\) 个数据点中确定 \(K\) 个聚类中心. 在 M-step 中, 通过第 (22) 式计算新的聚类中心:
\[\mub_k=\frac1{N_k}\sum_{i:z_i=k}\x_i\]