- 1. Introduction
- 2. SNE
- 3. t-SNE
- 4. 可视化
- 5. (TVCG 2020) t-viSNE: Interactive Assessment and Interpretation of t-SNE Projections
- 附录
- 参考文献
本文内容主要翻译自 Visualizating Data using t-SNE1.
1. Introduction
高维数据可视化是许多领域的都要涉及到的一个重要问题. 降维 (dimensionality reduction) 是把高维数据转化为二维或三维数据从而可以通过散点图展示的方法. 降维的目标是尽可能多的在低维空间保留高维数据的关键结构. 传统降维方法如 PCA2, MDS3 都是线性方法, 在降维过程中主要保证了不相似的点尽量远离的结构特征. 但是当高维数据处于低维非线性流形上时, 保证相似的点尽量接近更为重要, 而这在线性映射中通过难以做到.
目前已经有大量非线性降维技术, 可以参考 Lee 和 Verleysen 在 2007 年的综述论文4. 这里列举七种方法:
- Sammon mapping5
- Curvilinear components analysis, CCA6
- Stochastic Neighbor Embedding, SNE7
- Isomap8
- Maximum Variance Unfolding, MVU9
- Locally Linear Embedding, LLE10
- Laplacian Eigenmaps11
本文提出 t-SNE 用于可视化高维数据, 它可以保留高维数据的局部特征, 同时也能揭示数据的整体结构. \(\newcommand{\pjci}{p_{j\vert i}} \newcommand{\qjci}{q_{j\vert i}} \newcommand{\pij}{p_{ij}} \newcommand{\qij}{q_{ij}} \newcommand{\pji}{p_{ji}} \newcommand{\qji}{q_{ji}}\)
2. SNE
随机近邻嵌入 (stochastic neighbor embedding, SNE) 把高维数据点之间的欧氏距离转化为表示相似度的条件概率. 数据点 \(x_j\) 与 \(x_i\) 的相似度定义为条件概率 \(p_{j\vert i}\) , 它表示数据点 \(x_i\) 选择邻近点 \(x_j\) , 且该条件概率正比于在点 \(x_i\) 做高斯中心化后的概率密度, 如下式所示:
\[\pjci=\frac{\exp\left(-\Vert x_i-x_j\Vert^2/2\sigma_i^2\right)}{\sum_{k\neq i}\exp\left(-\Vert x_i-x_k\Vert^2/2\sigma_i^2\right)}\]其中 \(\sigma_i\) 是中心在 \(x_i\) 高斯分布的标准差. 如果两个点离得很近, \(p_{j\vert i}\) 就会比较大; 反之就会接近 0. 我们定义 \(p_{i\vert i}=0\) . 对于高维点 \(x_i\) 和 \(x_j\) 对应的低维点 \(y_i\) 和 \(y_j\) , 我们可以计算一个类似地相似度, 记为 \(q_{j\vert i}\) . 我们固定低维空间中用于计算 \(q_{j\vert i}\) 的高斯分布的标准差为 \(1/\sqrt2\) , 这样我们有:
\[\qjci=\frac{\exp\left(-\Vert y_i-y_j\Vert^2\right)}{\sum_{k\neq i}\exp\left(-\Vert y_i-y_k\Vert^2\right)}\]按照假设, 如果 \(q_{j\vert i}\) 可以正确建模高维数据点之间的相似度, 那么条件概率 \(p_{j\vert i}\) 和 \(q_{j\vert i}\) 应该是相等的. 因此 SNE 的目标就转化为减小这两个条件概率之间的误差. 一个自然的想法是利用 KL 散度 (Kullback-Leibler divergence) . 我们使用梯度下降法令 SNE 极小化所有数据点的 KL 散度, 损失函数定义为:
\[C=\sum_i KL(P_i\Vert Q_i)=\sum_i\sum_j \pjci\log\frac{\pjci}{\qjci}\]其中 \(P_i\) 表示给定数据点 \(x_i\) 时关于其他所有数据点的条件概率分布, 而 \(Q_i\) 表示给定降维后的数据点 \(y_i\) 时关于其他所有数据点的条件概率分布. 由于 KL 散度是非对称的, 所以我们有如下的观察:
- 如果用低维空间中距离远的两个点 ( \(\qjci\) 小) 来表示高维空间中距离近的两个点 ( \(\pjci\) 大 ), 那么就会得到一个较大的损失
- 如果用低维空间中距离近的两个点 ( \(\qjci\) 大) 来表示高维空间中距离远的两个点 ( \(\pjci\) 小 ), 那么就会得到一个较小的损失
从这两点观察可以总结出: SNE 损失函数目标是尽可能保持数据的局部结构 (即距离近的点在低维空间中映射的不能太远).
另外要考虑的是参数 \(\sigma_i\) 的选取. 由于数据点密度的不同, 我们不应该用单个 \(\sigma_i\) 的值来建模所有的数据点. 在数据稠密的区域, 用小的 \(\sigma_i\) 显然要比大的值更准确. 任意 \(\sigma_i\) 的值都对应一个概率分布 \(P_i\) , 它可以关联到熵, 随着 \(\sigma_i\) 的增大而增大 (表示数据点的分散程度). SNE 通过给定一个固定的困惑度 (perplexity) 后进行二分搜索来寻找 \(\sigma_i\) , 从而确定 \(P_i\). 这里定义困惑度 为:
\[Perp(P_i)=2^{H(P_i)}\]其中 \(H(P_i)\) 为香农熵:
\[H(P_i)=-\sum_j \pjci\log_2\pjci\]困惑度可以解释为有效邻近点个数的光滑化的测度. SNE 对困惑度的调整有一定鲁棒性, 典型值为 \(5\sim50\) .
公式 (3) 的极小化可以通过梯度下降法来计算. 其梯度为:
\[\frac{\partial C}{\partial y_i} = 2\sum_j (\pjci-\qjci+p_{i\vert j}-q_{i\vert j})(y_i-y_j)\]为了加速收敛并避免陷入局部极小值点, 在梯度下降的过程中要使用动量 (即加上先前梯度的指数衰减项):
\[\mathcal{Y}^{(t)}=\mathcal{Y}^{(t-1)}+\eta\frac{\partial C}{\partial \mathcal{Y}}+\alpha(t)\left(\mathcal{Y}^{(t-1)}-\mathcal{Y}^{(t-2)}\right)\]3. t-SNE
尽管 SNE 已经可以给出较好的数据可视化, 但它仍然受限于优化问题的困难和”拥挤问题”. 本节我们提出 t-SNE 来解决该问题. 与 SNE 相比, t-SNE 的损失函数有两点不同:
- 它使用了一种对称的损失函数 (梯度更简洁)
- 它使用了 t-分布代替高斯分布在低维空间表示两点间的相似度 (采用长尾分布来减轻”拥挤问题”)
3.1 对称 SNE
除了直接优化条件概率 \(p_{j\vert i}\) 和 \(q_{j\vert i}\) 之间的 KL 散度, 还可以优化两个联合分布 (高维空间的 P 分布和低维空间的 Q 分布) 的 KL 散度:
\[C=KL(P\Vert Q)=\sum_i\sum_j \pij\log\frac{\pij}{\qij}\]与之前类似, 我们令 \(p_{ii}=0,q_{ii}=0\) . 我们把这种 SNE 称为对称 SNE, 因为满足 \(\pij=\pji,\qij=\qji,\forall i,j\). 在对称 SNE 中, 低维空间两点的相似度为:
\[\qij=\frac{\exp\left(-\Vert y_i-y_j\Vert^2\right)}{\sum_{k\neq l}\exp\left(-\Vert y_k-y_l\Vert^2\right)}\]类似地高维空间两点相似度为:
\[\pij=\frac{\exp\left(-\Vert x_i-x_j\Vert^2/2\sigma^2\right)}{\sum_{k\neq l}\exp\left(-\Vert x_k-x_l\Vert^2/2\sigma^2\right)}\nonumber\]注意到如果有离群点 \(x_i\), 那么 \(\pij\) 的值就会对所有的 \(x_j\) 都非常小 (因为 \(\Vert y_i-y_j\Vert^2\) 非常大) , 这样对损失函数的影响就很小, 导致低维空间中无法很好的捕获离群点和其他点之间的关系. 为了避免这个问题, 我们把联合概率 \(\pij\) 定义为:
\[\pij=\frac{\pjci+p_{i\vert j}}{2n}\]这保证了对于所有的 \(x_i\) , 都有 \(\sum_j\pij>\frac1{2n}\) , 从而每一项都会对损失函数有可观的贡献. 在低维空间中对称 SNE 的计算直接使用 (9) 式. 对称 SNE 的一个主要的优点是梯度简洁容易计算:
\[\frac{\partial C}{\partial y_i}=4\sum_j(\pij-\qij)(y_i-y_j)\]梯度的计算方式见附录.
3.2 拥挤问题
先考虑一种简单的情况: 一族点分布在一个二维流形上, 其分布呈近似的直线型, 该流行嵌入到高维空间中. 那么我们可以比较容易地对点之间的距离在二维空间中建模.
再考虑一种复杂的情况: 流行有10个本征维度并嵌入到一个更高维的空间中, 此时对点的距离进行建模就会遇到问题:
- 比如, 在10维空间, 存在11个点构成的正多面体, 任意两点之间的距离都相等. 这种情况下不可能在二维空间中对其建模.
- 比如, 一个点为高维球心, 其余点均匀的分布在高维球的表面, 这是个10维流行, 那么对球心到其他点在低维空间的建模也会遇到困难, 称为拥挤问题:
- 在高维空间中距离近的点被映射到低维空间的距离仍然可以比较近
- 在高维空间中距离远的点被映射到低维空间后无法使得距离足够远, 即低维空间无法分散地容纳高维空间中远距离的点, 这是由降维造成的, 从而这些远距离的点在高维空间可能是分散的, 但在低维空间就挤在了一起.
- SNE 方法并没有解决这个问题. 要解决该问题, 需要对低维空间用于建模的分布做一定的调整.
3.3 调整低维空间的分布
因为对称 SNE 实际上匹配的是高维空间和低维空间数据的联合分布而非距离, 因此我们可以通过以下的方法来解决拥挤问题:
- 在高维空间, 我们用高斯分布把距离转化为概率
- 在低维空间, 我们用长尾分布把距离转化为概率
这样高维空间里的中等距离映射到低维空间中有一个较远的距离, 这样可以避免不相似的点离得太近. 在 t-SNE 中, 我们使用自由度为 1 的 t-分布 (也称为柯西分布) 作为低维空间中的长尾分布, 这样联合概率就变为:
\[\qij=\frac{(1+\Vert y_i-y_j\Vert^2)^{-1}}{\sum_{k\neq l}(1+\Vert y_k-y_l\Vert^2)^{-1}}\]我们采用自由度为 1 的 t-分布是因为 \((1+\Vert y_i-y_j\Vert^2)^{-1}\) 在 \(\Vert y_i-y_j\Vert\) 距离较大时接近平方倒数. 这使得联合分布的低维表示对于低维尺度的缩放有着一定的不变性. 我们选择 t-分布的原因是它是一种无限的高斯混合分布, 但计算概率密度时却不再需要计算指数, 可以降低计算复杂度.
高维分布 \(P\) 和低维 t-分布 \(Q\) 的 KL 散度的梯度可以根据附录类似地计算:
\[\frac{\partial C}{\partial y_i}=4\sum_j(\pij-\qij)(y_i-y_j)(1+\Vert y_i-y_j\Vert^2)^{-1}\]下图展示了 \(\Vert x_i-x_j\Vert\) 和 \(\Vert y_i-y_j\Vert\) 和梯度的关系, 三幅图分别为对称 SNE, UNI-SNE 和 t-SNE 的结果.
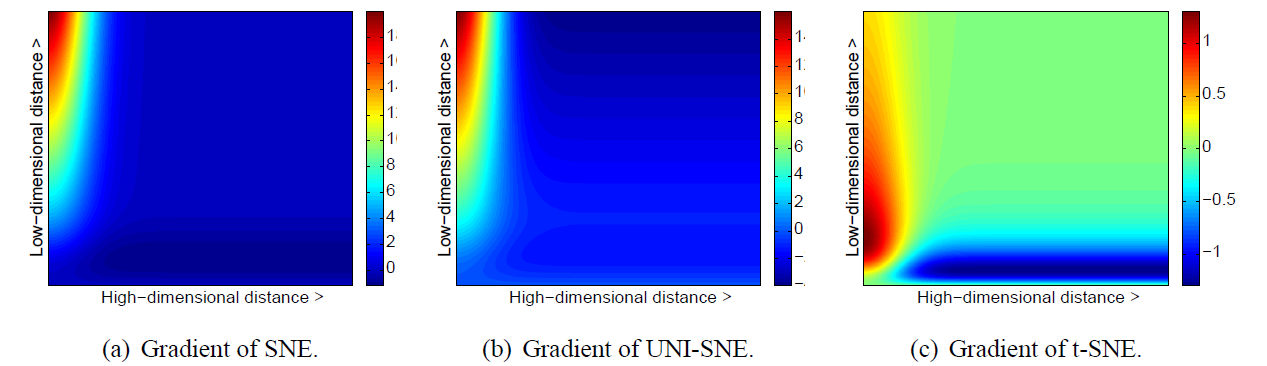
图 1. 三种类型 SNE 的梯度作为高维点距和低维点距函数的热力图
其中正梯度表示两点之间存在引力, 负梯度表示斥力. 从上图可以发现 t-SNE 有以下优点:
- t-SNE 梯度对于低维中邻近的不相似点有较大的斥力, 相比于 SNE 和 UNI-SNE 在分布上更为均匀合理
- t-SNE 的斥力是有限的, 不像 UNI-SNE 那样随着距离无限增大
3.4 算法
t-SNE 的一种简单算法
数据: 数据集 \(\mathcal{X}=\{x_1,x_2,\dots,x_n\}\)
损失函数的参数: 困惑度 \(Perp\)
优化算法的参数: 迭代次数 \(T\) , 学习率 \(\eta\) , 动量 \(\alpha(t)\)
结果: 低维数据表示 \(\mathcal{Y}^{(T)}=\{y_1,y_2,\dots,y_n\}\)
begin
使用 \(Perp\) 计算相似度 \(\pjci\)
令 \(\pij=\frac{\pjci+p_{i\vert j}}{2}\)
从 \(\mathcal{N}(0,10^{-4}I)\) 中采样初始结果 \(\mathcal{Y}^{(0)}=\{y_1,y_2,\dots,y_n\}\)
for \(t=1\) to \(T\) do
计算低维相似度 \(\qij\)
计算梯度 \(\frac{\partial C}{\partial \mathcal{Y}}\)
更新 \(\mathcal{Y}^{(t)}=\mathcal{Y}^{(t-1)}+\eta\frac{\partial C}{\partial\mathcal{Y}}+\alpha(t)(\mathcal{Y}^{(t-1)}-\mathcal{Y}^{(t-2)})\)
end
end
4. 可视化
代码实现: Github: Jarvis73/MachineLearning
代码中包含了根据 blog 及其 Github: nlml/tsne_raw 的实现, 以及基于 sklearn 的实现. 后者在执行速度和效果上都有很大幅度的提升.
- sklearn 的实现

图 2. sklearn: mnist, lr=10, perplexity=20, n_pts=1000, n_iter=500
- 自行实现的结果
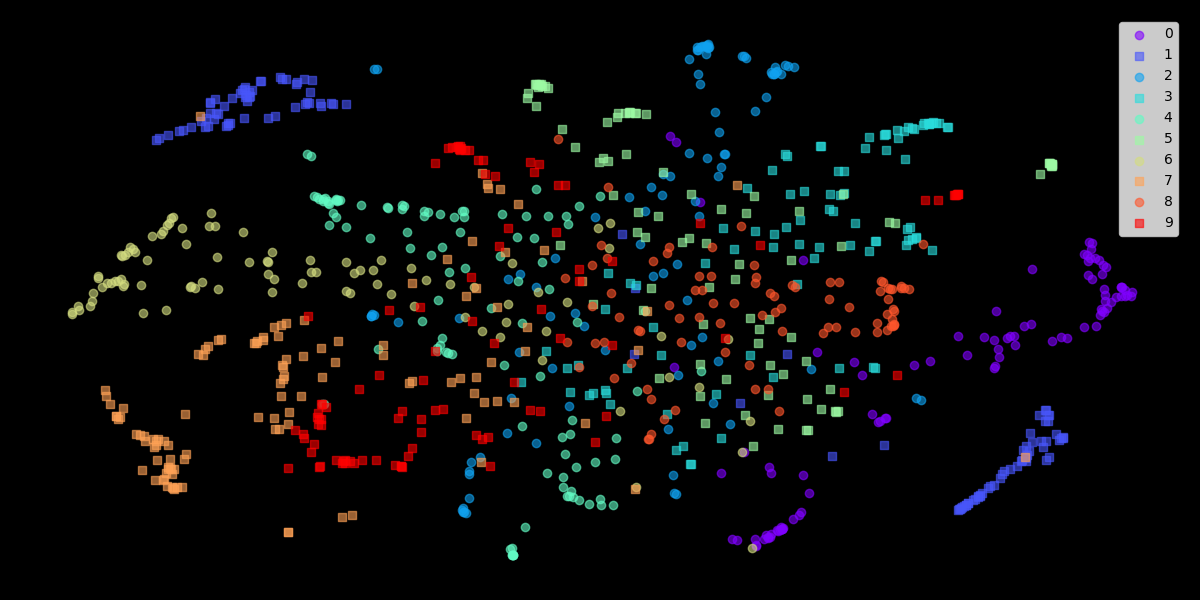
图 3. raw: mnist, lr=10, perplexity=20, n_pts=1000, n_iter=500
- Mnist 通过神经网络学习到的特征
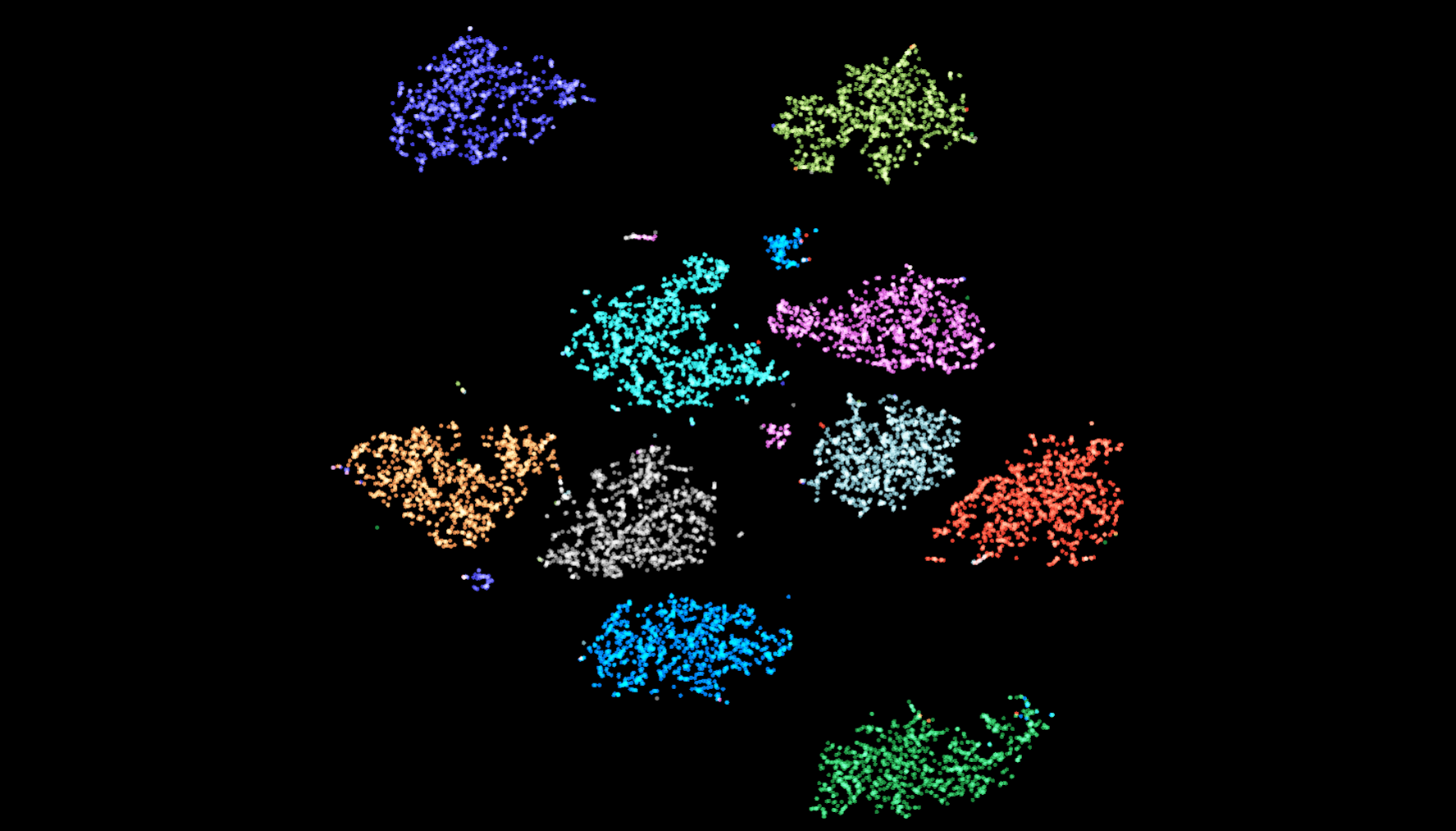
图 4. [Tensorboard 中的 projector 工具得到的结果](https://projector.tensorflow.org/)
5. (TVCG 2020) t-viSNE: Interactive Assessment and Interpretation of t-SNE Projections
t-viSNE12 是一个用于交互式地研究和探索超参数、距离、近邻、密度和损失与 t-SNE 结果的可视化系统.
5.1 引言
在 Wattenberg 等人的研究13 中我们知道, t-SNE 中有一些值得注意的陷阱:
5.1.1 t-SNE 对超参数很敏感

图 5. 不同困惑度下 t-SNE 的结果

图 6. 不同迭代次数下 t-SNE 的结果
5.1.2 高维空间数据的方差不会反映在低维表示中
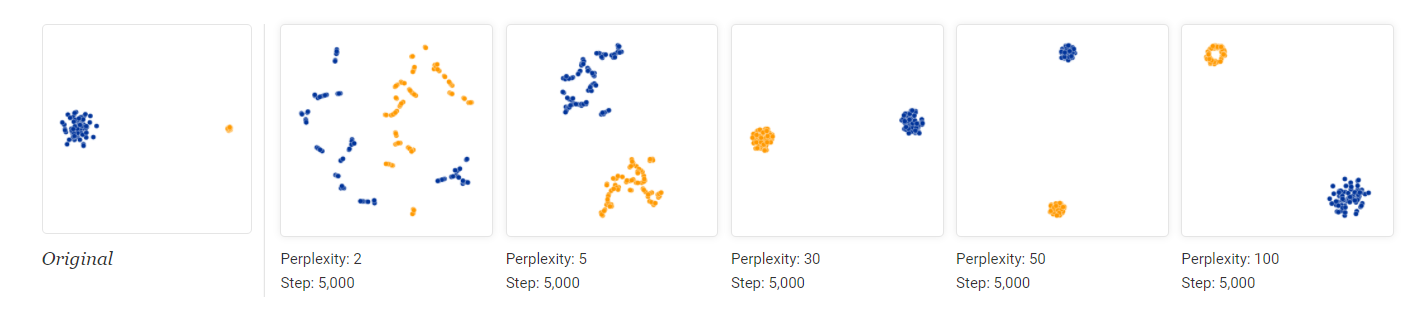
图 7. 高维数据的低维表示不会保留方差信息
5.1.3 聚类间的距离没有意义

图 8. 三个高斯分布, 每个包含50个点
可以发现困惑度达到50的时候聚类间的全局关系反映出来了.

图 9. 三个高斯分布, 每个包含200个点
但是当点的数量增加到200时, 困惑度再大也没有反映出全局关系.
5.1.4 随机噪声看起来不一定那么随机
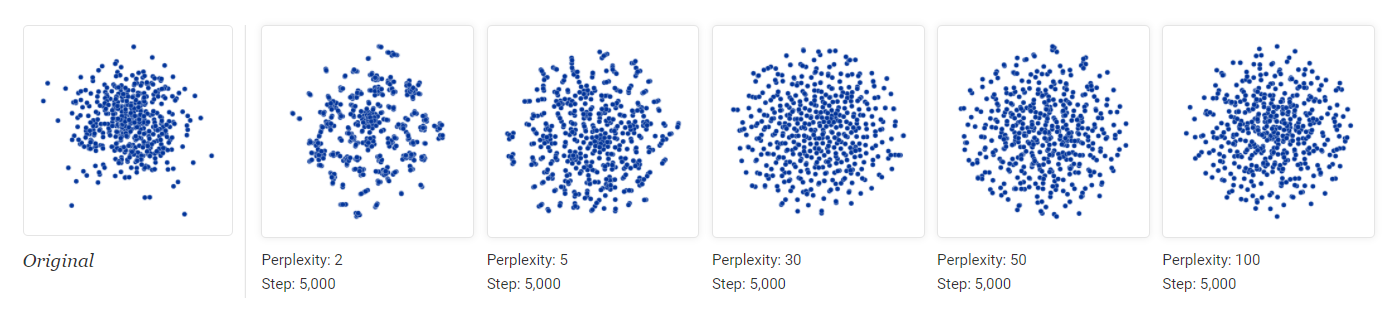
图 10. 一个高斯分布, 低困惑度的时候随机噪声也会形成一些小块
在 t-SNE 中, 低困惑度的时候往往会产生一些小块. 要意识到这些小块并不代表任何含义, 它们往往是随机噪声导致的.
5.1.5 有时候会出现一些特殊的形状
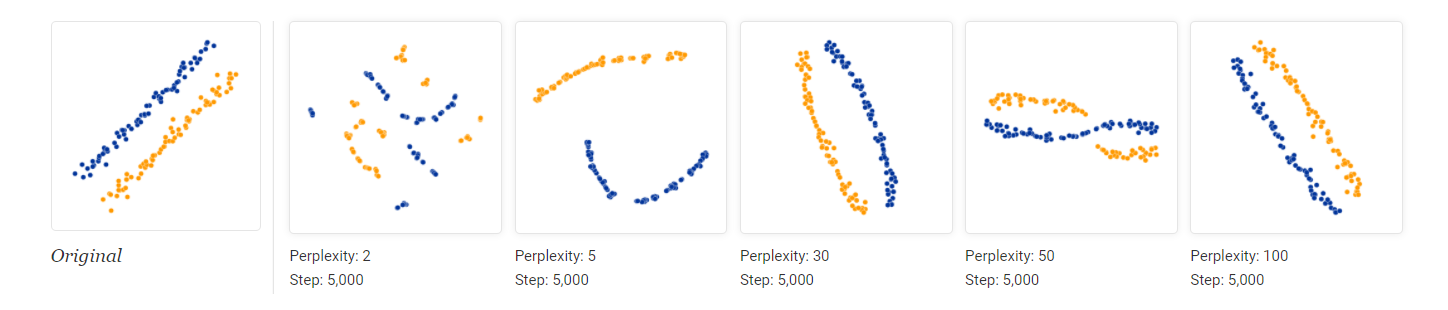
图 11. 出现了奇怪的形状
尽管这些建议对于避坑有一定用处, 但是主要讨论了合成的数据. 遇到真实数据的时候, 其分布是未知的, 此时难以从中获得可靠的超参数调整信息.

图 12. |
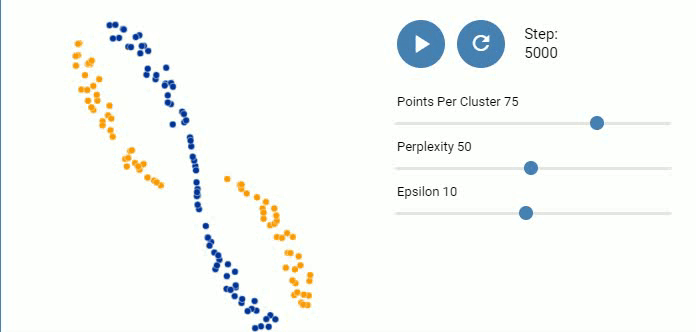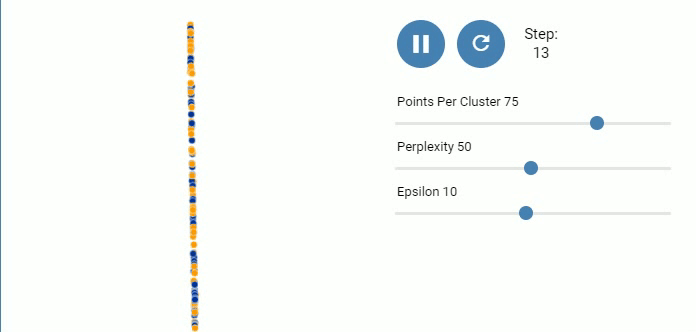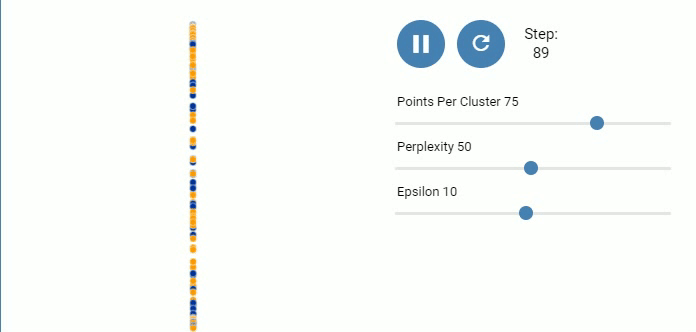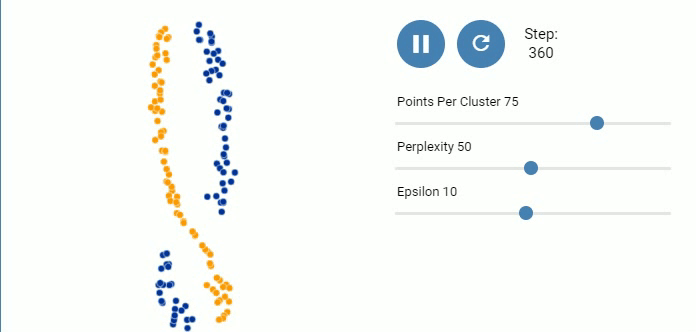
图 13. |
5.2 相关工作
略.
5.3 t-viSNE
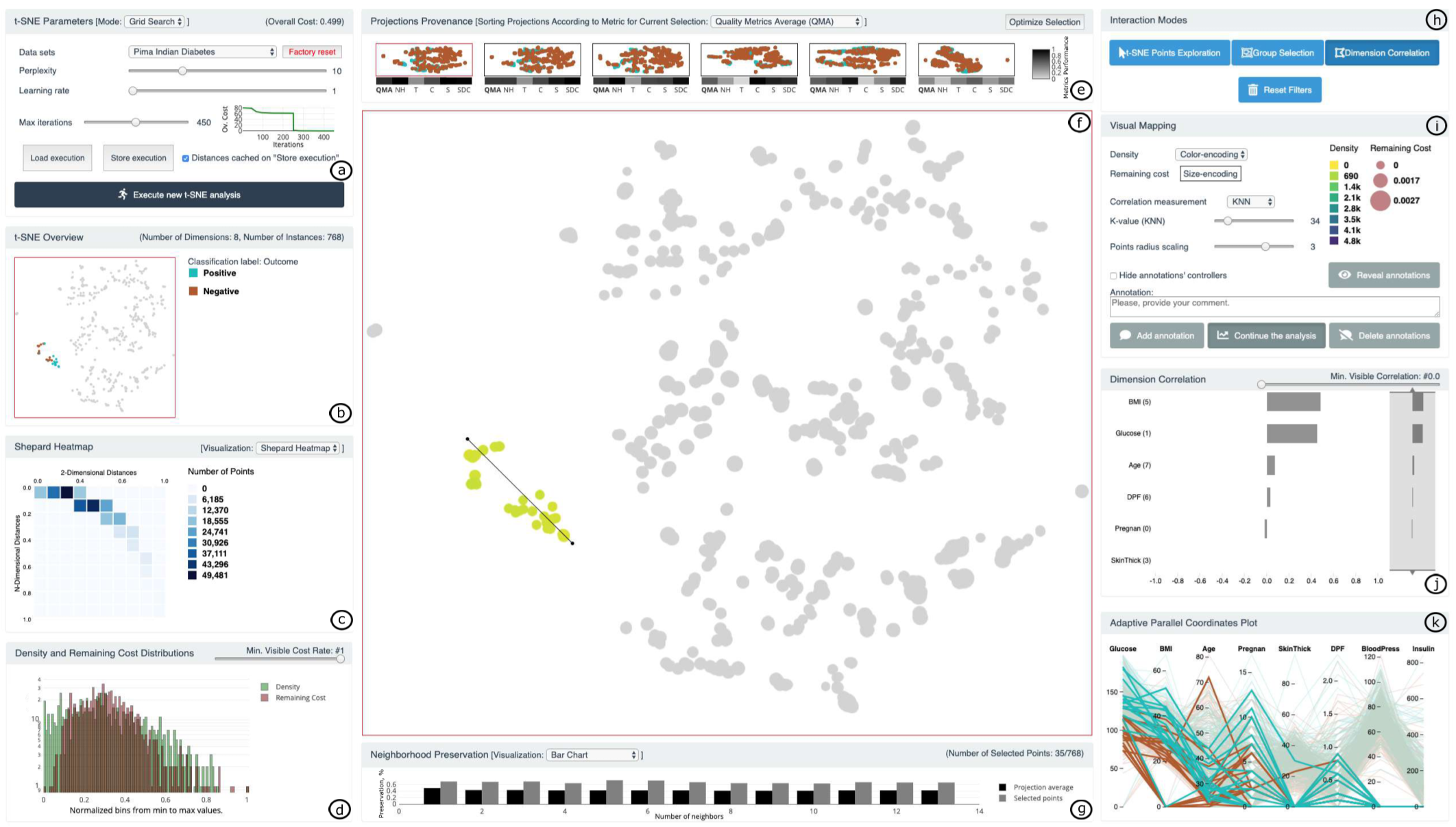
图 14. t-viSNE 系统概览
t-viSNE 系统的设计包含四个目标:
- G1: 超参数探索
- G2: 概览
- G3: Quality
- G4: 维度
G1: 超参数探索
如上图(a). 功能: 网格搜索/单参数运行 (困惑度, 学习率, 最大迭代次数). 500 个搜索格点, 最终选择 25 个展示缩略图 (通过 K-Medoids 聚类出 25 个, 使用 Procrustes 距离).

图 15. 网格搜索的结果展示
同时下面利用灰度热力图展示了五种质量评估的指标和一个平均指标. 下图展示了通过连续性排序的结果. 同时我们选择第四幅图, 它具有较高的连续性和不错的平均质量.
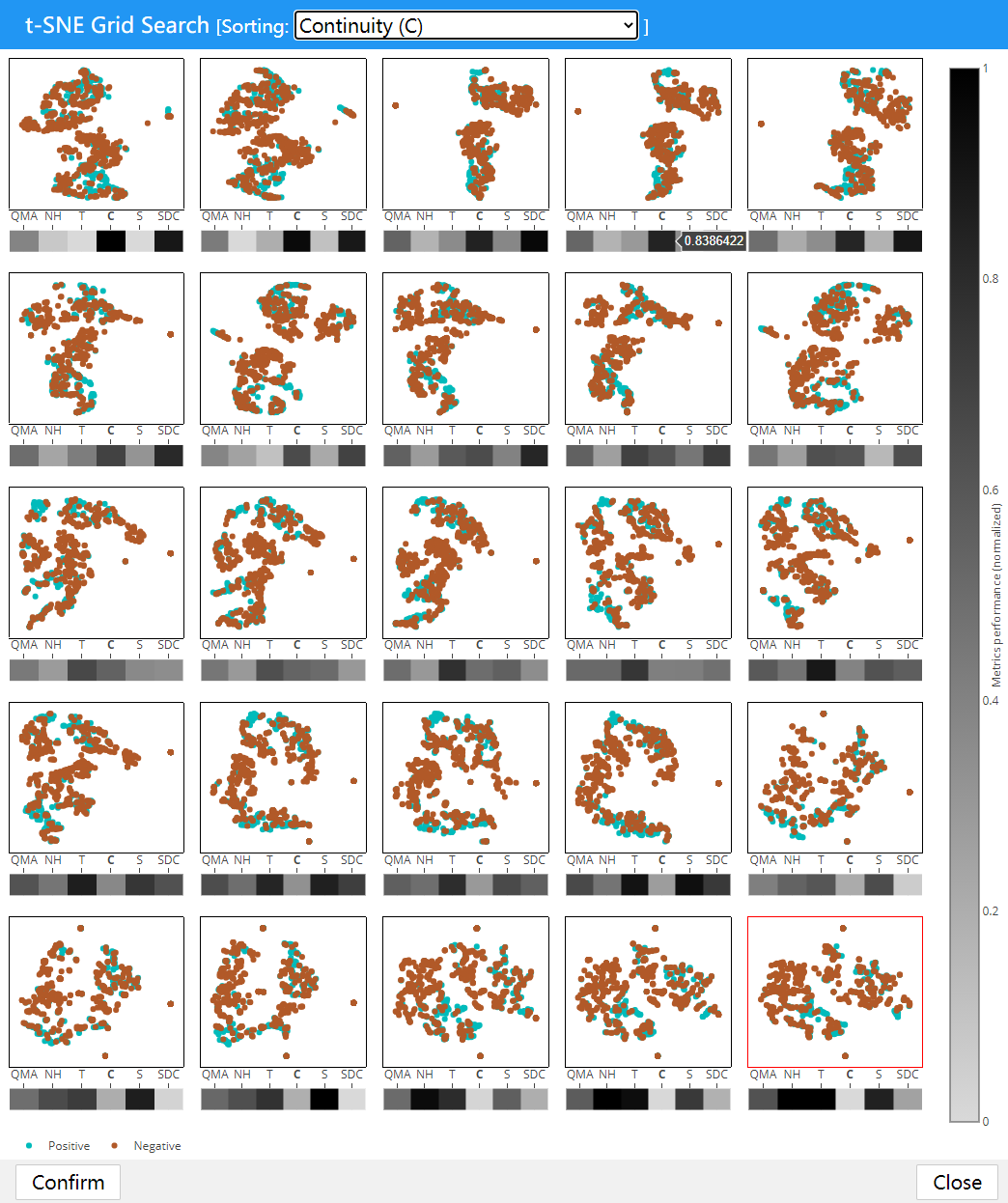
图 16. 通过连续性排序
选择后点击 Confirm 确认回到主面板, 然后点击中间上方的前六个结果的第4个(我们选择的), 即可在主视图看到降维结果.
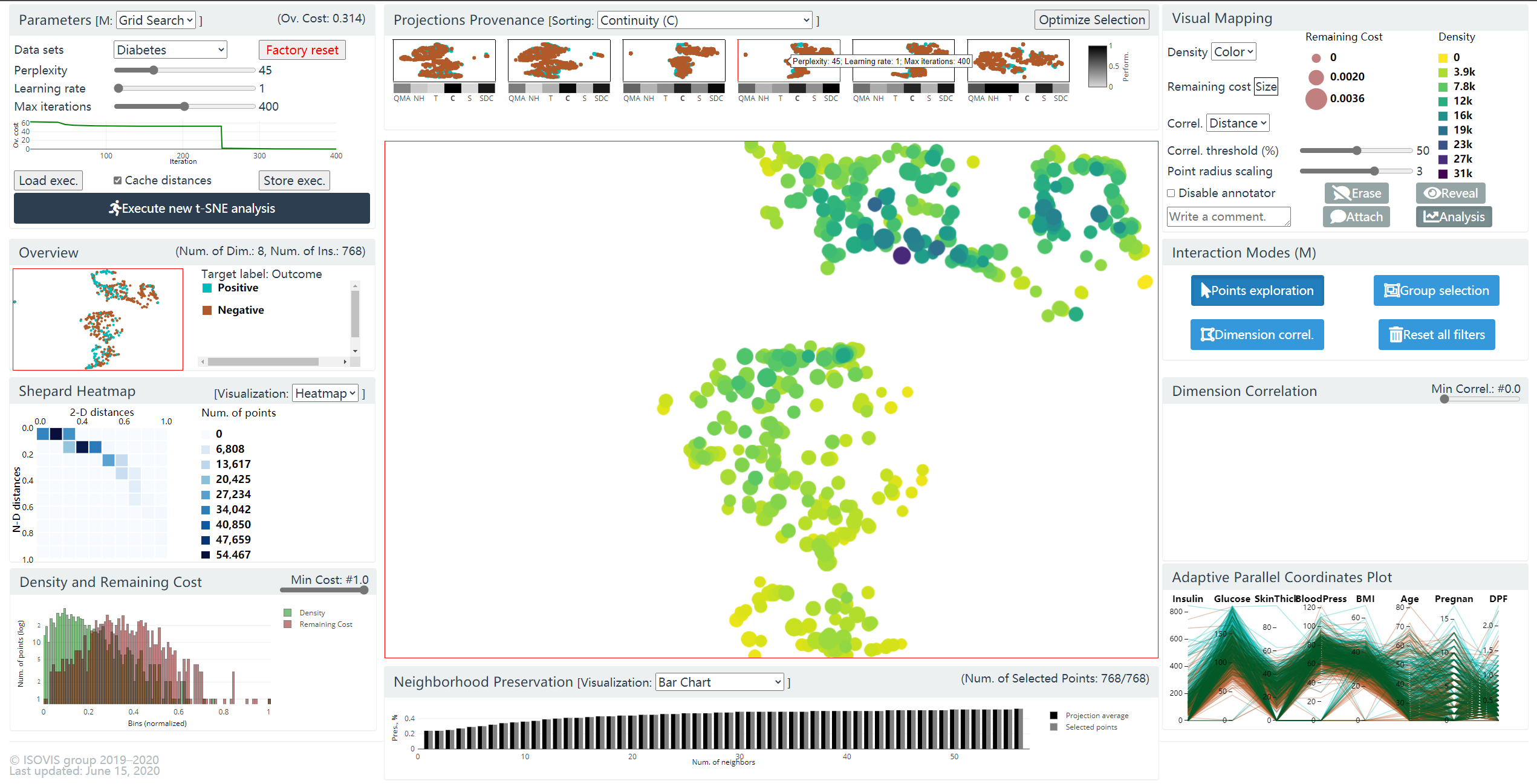
图 17. 中间的面板为主视图
G2: 主视图
主视图是一个交互式的散点图. 四种交互模式:
- Point Exploration 模式 (默认): 支持平移, 缩放, 鼠标在点上悬浮时可以展示点的各个维度的属性.
- Group Selection 模式: 套索选择, 其他视图可联动
- Dimension Corresion
- Reset Filters
G3: Quality
Shepard Heatmap
Y-轴表示 N 维空间点之间的距离分布, X-轴表示二维空间点之间的距离分布. 下图中分布偏上, 说明高维空间聚集起来的点在低维空间中被分散开了.
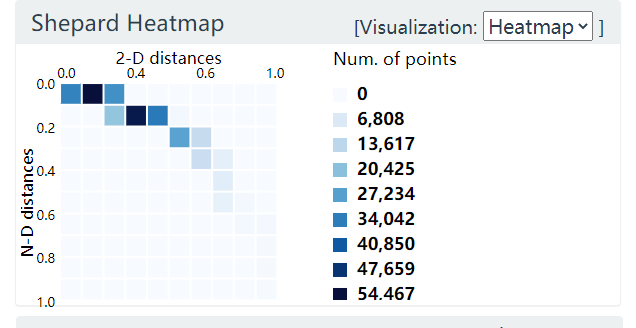
图 18. Shepard Heatmap
进一步, 如果分布在中轴线附近, 则说明高低维空间点的距离保持的比较好. (尽管t-SNE不保距); 如果分布在中轴线下方, 则说明高维空间分散的点在低维空间中聚集起来了.
Visual Mapping
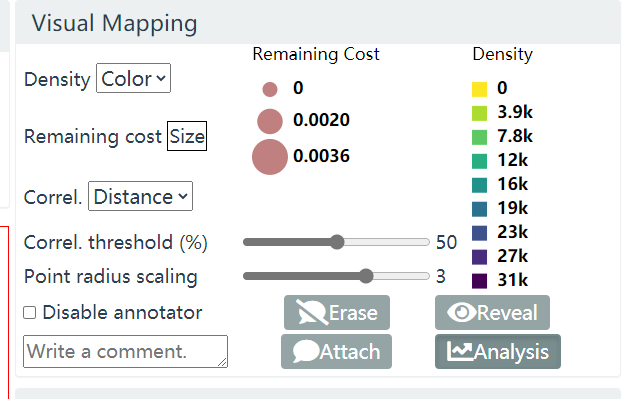
图 19. Visual Mapping
Visual Mapping 面板包含 Density, Remaining Cost 两项主要功能.
- Density
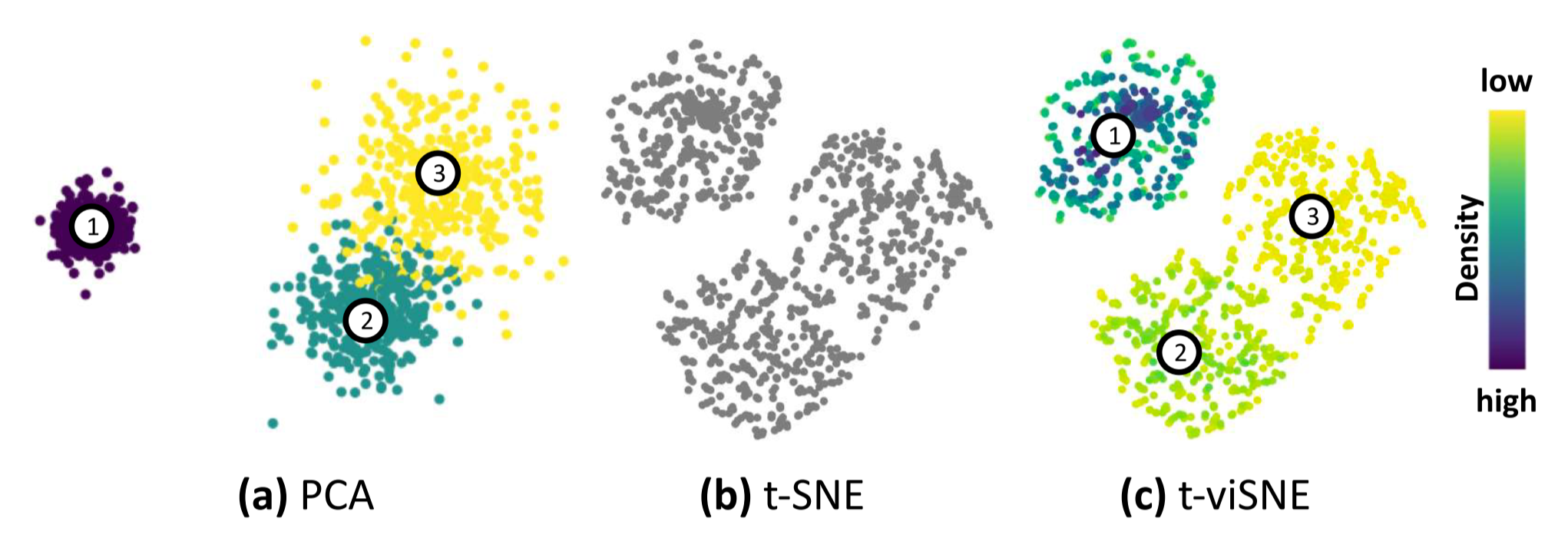
图 20. Visual Mapping 中 Density 的作用
由于 t-SNE 在降维前每个点都有一个 sigma 来表示密度, 而降维后没有了 sigma, 这样 t-SNE 就丢失了密度信息. 因此本文使用颜色来编码 Density 反映在降维后的点上. 这样在上图(c)中, 聚类2和3就可以通过密度来表明是是两个类, 而不是一个大类(b).
- Remaining Cost
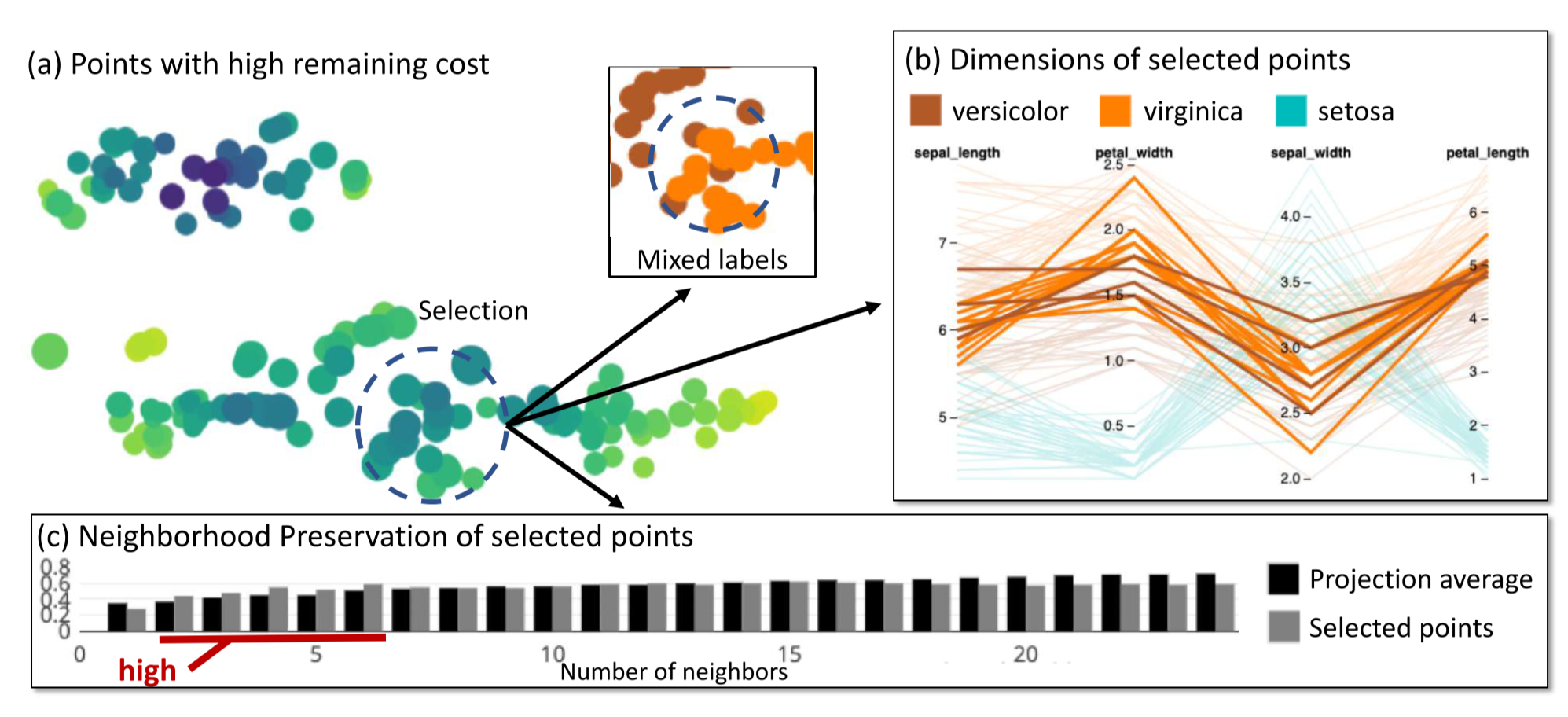
图 21. Visual Mapping 中 Remaining Cost 的作用
Remaining Cost 这里是用点的大小来表示的. 如上图是鸢尾花的降维结果, 选中的圆圈中的点的较大, 表明这里的点最终的损失较大. 实际上这里是两个类别的交界处. 进一步通过平行坐标系也可以看出这些点位于两个类别交界处.
Neighborhood Preservation
在降维中, 相比于保距降维, 人们往往会优先考虑保近邻. 因此 t-SNE 中高维点采用高斯分布来建模距离, 从而保持近邻. 因此在 t-SNE 中判断保近邻的效果也是一个重要的评估 t-SNE 质量的指标.
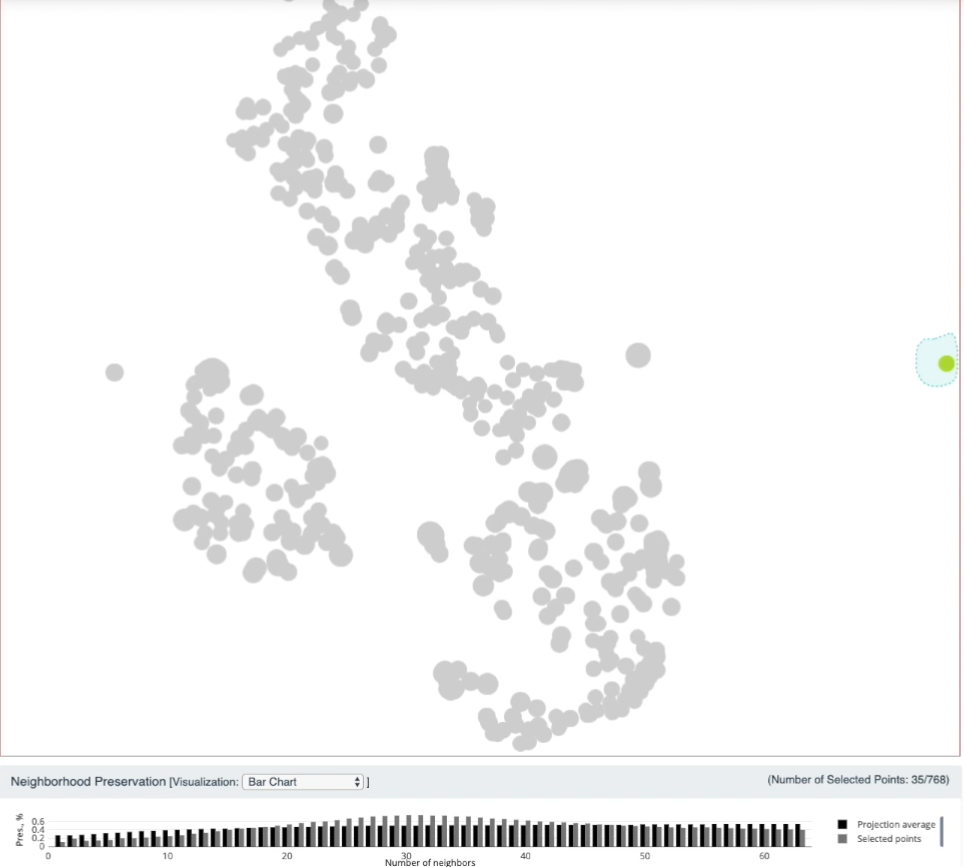
图 22. 保近邻的效果, 选中点集与平均进行比较
在 Neighborhood Preservation 视图中, 黑色柱形图表示 k 近邻的保持程度. 随着 k (横轴坐标)增大, 近邻保持度越高, 这是符合直觉的. 在上图中选出的点集的近邻保持程度用灰色柱形图表示. 上图中k=30 左右时灰色柱高于黑色柱, 说明这个降维结果中, 选中的点集在 k=30 个近邻的保持度上比较好(高于平均水平).
G4: Dimensions
自适应平行坐标系 Adaptive PCP
显示选中的点集的最多8个属性. 显示哪些属性以及显示的顺序都是自适应的. 本文对选中的点集应用 PCA 降维, 选出特征值的那个特征值对应的特征向量(该轴方差最大), 该向量的每个维度表示了使用原始的维度来解释最大方差的重要程度. 因此按照该特征向量的值大小, 对原始的轴进行排序, 选出前 8 个按顺序绘制 PCP.
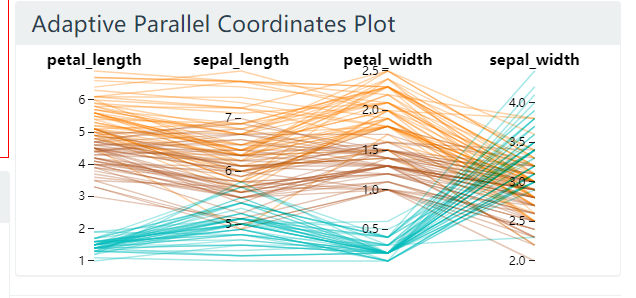
图 23. 鸢尾花数据集, 选择点集之前
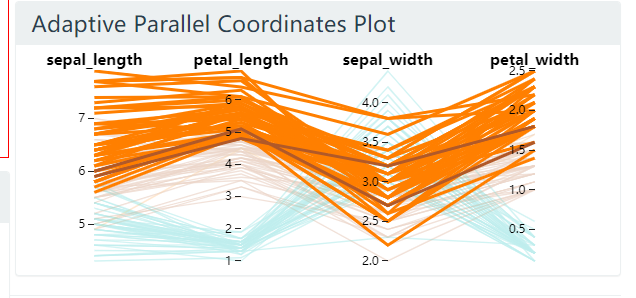
图 24. 鸢尾花数据集, 选择点集之后
选择点集之后, sepal_length 这一属性排到了最前面.
Dimension Correlation
对聚类结果的解释是 t-SNE 重要的一环. 但根据前文的讨论, t-SNE 可以产生各种聚类的形状, 因此并不一定反映真实的高维形状. 因此自然地我们要允许用户对其发现的特殊形状进行探索, 查看是否有高度相关的维度.
用户首先在主视图中绘制连续的线段来表示其发现的特殊形状, 然后程序自动根据设定的距离 rho 提取线段周边的点, 并投影到线段上, 从而这些点就可以拥有”用户定义”的顺序. 然后把用户定义的顺序和这些点在每个维度上的顺序之间的相关性通过 Spearman’s rank correlation coefficient 进行度量, 得到 dimension correlation 的系数. 从而反映出用户给定的特殊形状主要与哪些维度是高度相关的.
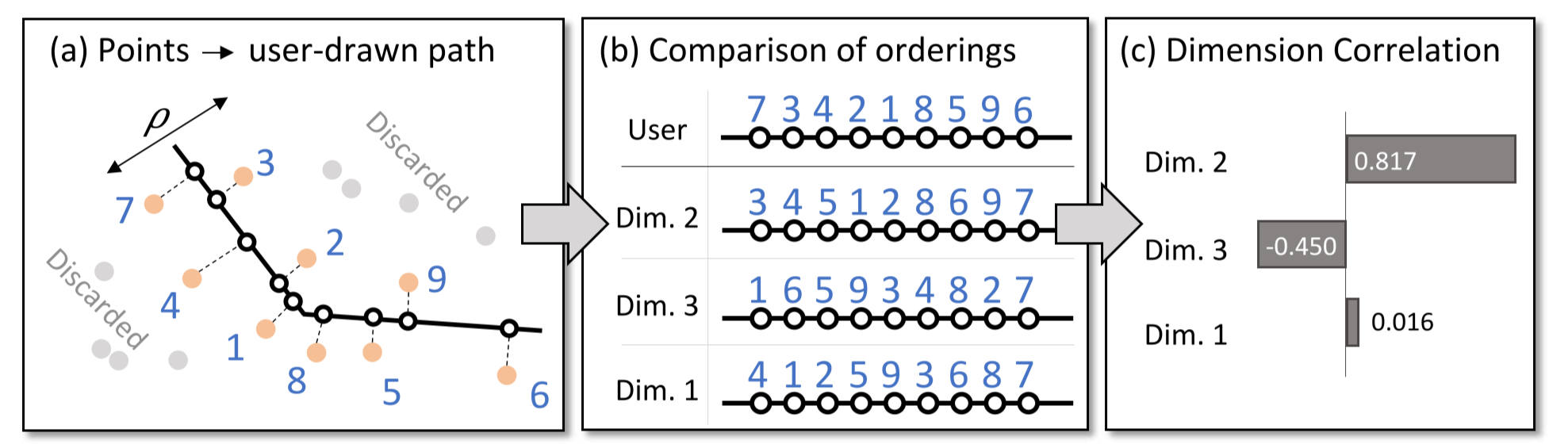
图 25. 维度相关性工具
下面我们给出乳腺癌良恶性聚类的一个例子.
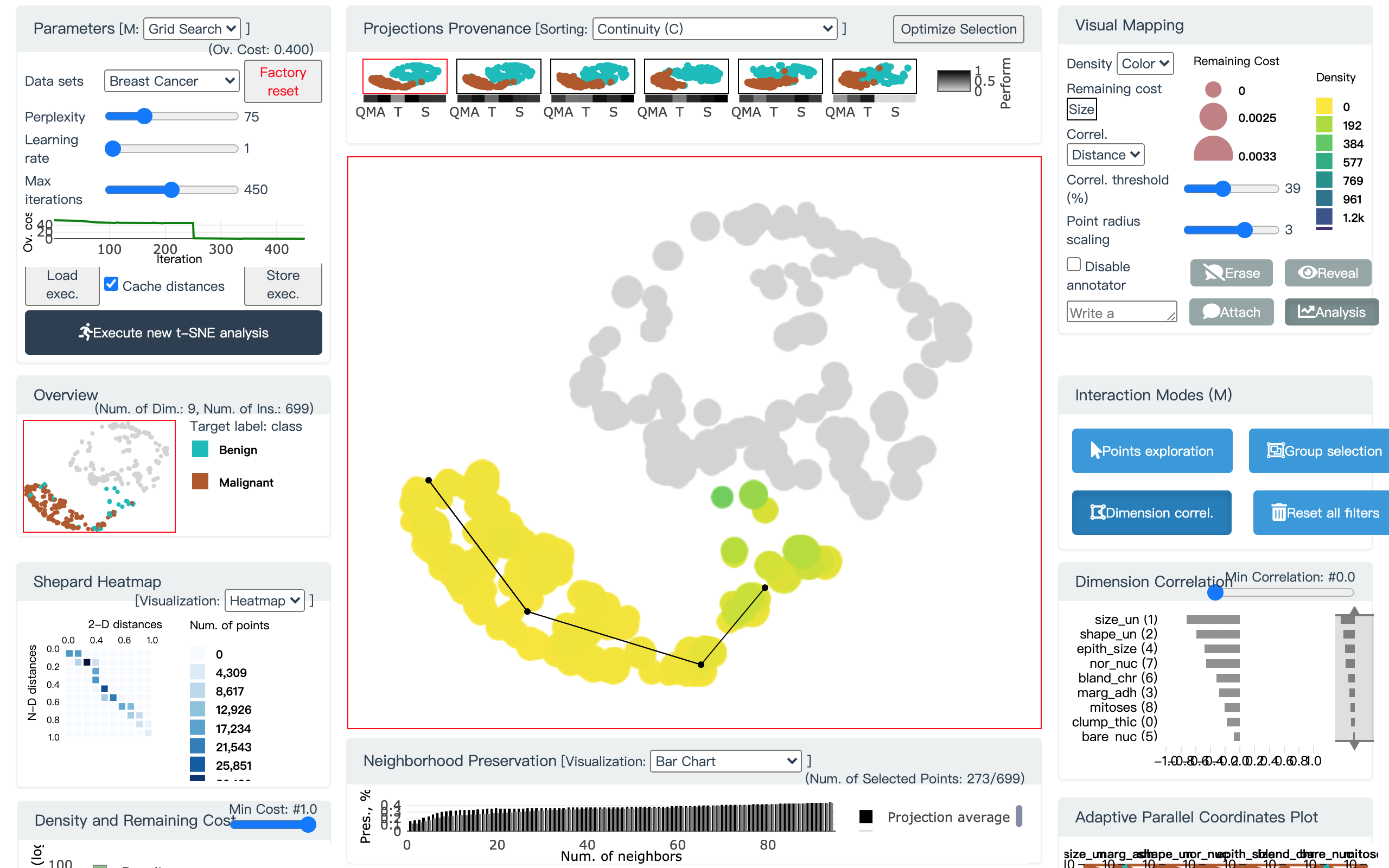
图 26. DC 工具, 用户添加线段
然后点击 Dimension Correlation 面板中相关度最高的维度, 这样主视图的配色用最相关的维度进行重编码
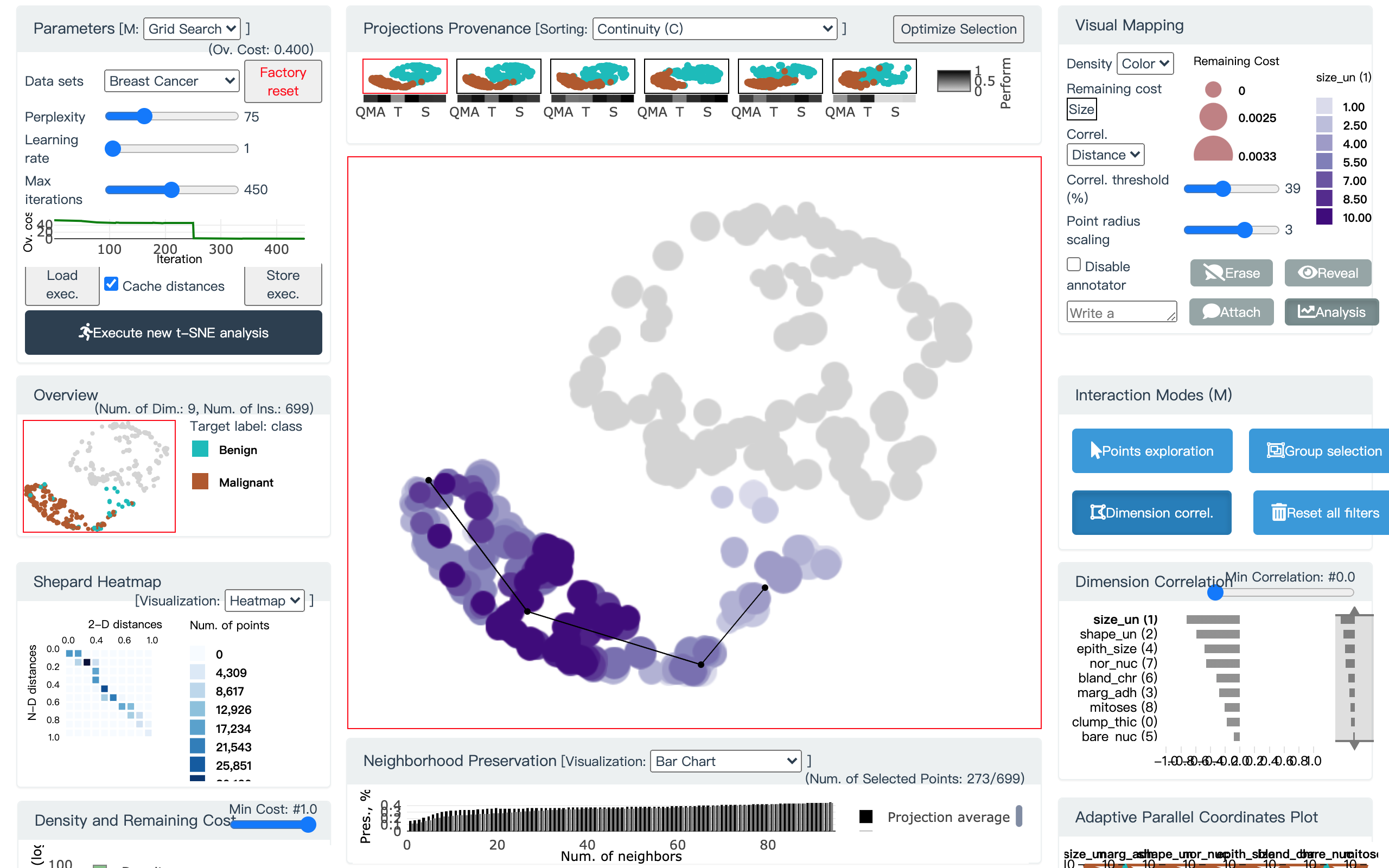
图 27. 主视图的配色用最相关的维度进行重编码
附录
公式 (11) 的梯度计算.
我们把要用到的表达式先列在前面:
- 高维空间数据点的相似度为 \(p_{ij}\)
- 低维空间数据点的相似度为
- t-SNE 损失函数 (公式 (11)) 为
为简化计算, 我们定义两个辅助变量
\[\begin{align} d_{ij} &=\Vert y_i-y_j\Vert^2 \\ Z &=\sum_{j\neq l}\exp(-d_{kl}) \end{align}\]其中 \(Z\) 就是 \(q_{ij}\) 的分母, 所以有 \(q_{ij}Z=\exp(-d_{ij})\) .
注意到当 \(y_i\) 变化一个微元时, 只有距离 \(d_{ij}\) 和 \(d_{ji}\) 发生变化, \(\forall j\) . 因此 \(C\) 关于 \(y_i\) 的梯度为:
\[\begin{align}\nonumber \frac{\partial C}{\partial y_i} &= \sum_j\left(\frac{\partial C}{\partial d_{ij}}\frac{\partial d_{ij}}{\partial y_i} + \frac{\partial C}{\partial d_{ji}}\frac{\partial d_{ji}}{\partial y_i}\right) \\ \nonumber &= 2\sum_j\frac{\partial C}{\partial d_{ij}}\frac{\partial d_{ij}}{\partial y_i} \qquad\qquad \Longleftarrow \qquad\qquad d_{ij}=d_{ji} \\ \nonumber &= 2\sum_j\frac{\partial C}{\partial d_{ij}}\frac{\partial(\Vert y_i-y_j\Vert^2)}{\partial y_i} \\ &= 4\sum_j\frac{\partial C}{\partial d_{ij}}(y_i-y_j) \end{align}\]接下来计算 \(\frac{\partial C}{\partial d_{ij}}\) . 由于损失函数第一项关于 \(d_{ij}\) 为常数, 因此只计算第二项的导数:
\[\begin{align} \frac{\partial C}{\partial d_{ij}} \nonumber &= -\sum_{k\neq l}p_{kl}\frac{\partial(\log q_{kl})}{\partial d_{ij}} \\ \nonumber &= -\sum_{k\neq l}p_{kl}\frac{\partial(\log q_{kl}Z-\log Z)}{\partial d_{ij}} \\ \nonumber &= -\sum_{k\neq l}p_{kl}\left(\frac1{q_{kl}Z}\frac{\partial(\exp(-d_{kl}))}{\partial d_{ij}}-\frac1Z\frac{\partial Z}{\partial d_{ij}}\right) \\ \nonumber &= \frac{\pij}{\qij Z}\exp(-d_{ij})-\sum_{k\neq l}p_{kl}\frac{\exp(-d_{ij})}{Z} &&\Longleftarrow\quad \frac{\partial(\exp(-d_{kl}))}{\partial d_{ij}}\neq 0 \text{ iff } d_{kl}=d_{ij} \\ \nonumber &= \pij - \sum_{k\neq l}p_{kl}\frac{\exp(-d_{ij})}{Z} &&\Longleftarrow\quad \qij Z=\exp(-d_{ij}) \\ &= \pij - \qij &&\Longleftarrow\quad \sum_{k\neq l}p_{kl}=1,\;\; \qij Z=\exp(-d_{ij}) \end{align}\]综合以上两式的推导可得
\[\frac{\partial C}{\partial y_i}=4\sum_j(\pij-\qij)(y_i-y_j)\]参考文献
-
Visualizing Data using t-SNE
Laurens van der Maaten, Geoffrey Hinton
[html], [pdf], Journal of machine learning research, 2008, 9(Nov): 2579-2605. ↩ -
Analysis of a complex of statistical variables into principal components
Hotelling H
[html], Journal of educational psychology, 1933, 24(6): 417. ↩ -
Multidimensional scaling: I. Theory and method
Torgerson W S.
[pdf], Psychometrika, 1952, 17(4): 401-419. ↩ -
Nonlinear dimensionality reduction of data manifolds with essential loops
Lee J A, Verleysen M.
[pdf], Neurocomputing, 2005, 67: 29-53. ↩ -
A nonlinear mapping for data structure analysis
Sammon J W.
[html], IEEE Transactions on computers, 1969, 100(5): 401-409. ↩ -
Curvilinear component analysis: A self-organizing neural network for nonlinear mapping of data sets
Demartines P, Hérault J.
[html], IEEE Transactions on neural networks, 1997, 8(1): 148-154. ↩ -
Stochastic neighbor embedding
Hinton G E, Roweis S T.
[pdf], In NIPS 2003: 857-864. ↩ -
A global geometric framework for nonlinear dimensionality reduction
Tenenbaum J B, De Silva V, Langford J C.
[pdf], science, 2000, 290(5500): 2319-2323. ↩ -
Learning a kernel matrix for nonlinear dimensionality reduction
Weinberger K Q, Sha F, Saul L K.
[html], In ICML. 2004: 106. ↩ -
Nonlinear dimensionality reduction by locally linear embedding
Roweis S T, Saul L K.
[html], science, 2000, 290(5500): 2323-2326. ↩ -
Laplacian eigenmaps and spectral techniques for embedding and clustering
Belkin M, Niyogi P.
[pdf], In NIPS. 2002: 585-591. ↩ -
t-viSNE: Interactive Assessment and Interpretation of t-SNE Projections
Angelos Chatzimparmpas, Rafael Messias Martins, Andreas Kerren
[html], [pdf], [code], In TVCG 2020. 26(8): 2696-2714 ↩ -
How to Use t-SNE Effectively
Wattenberg, Martin and Viégas, Fernanda and Johnson, Ian
[html], In Distill. 2016. Online. ↩