处理复杂系统的两个原理:
- 模块化原理
- 抽象化原理
– Michael Jordan
\(\newcommand{\x}{\mathbf{x}} \newcommand{\tb}{\boldsymbol{\theta}}\) 假设我们观测到了多个互相关联的变量, 如文档中的单词, 图像中的像素, 或者基因. 那么我们如何紧凑的表示多个关联变量的联合分布 \(p(\x\vert\tb)\) 呢? 我们如何使用这个分布在给定一些变量之后推理另一些变量呢?
本文内容来自 Machine Learning: A Probabilistic Perspective 的第 10 章 Directed Graphical Models (Bayes Nets)1. 原书错误修订2. 其他资料3.
1. 介绍
1.1 链式法则
根据概率的链式法则, 我们有
\[p(\x_{1:V})=p(x_1)p(x_2\vert x_1)p(x_3\vert x_2,x_1)p(x_4\vert x_1,x_2,x_3)\dots p(x_V\vert x_{1:V-1})\]其中 \(V\) 是变量的个数, 为了简便, 我们省略掉了条件变量 \(\tb\) .
假设所有变量都有 \(K\) 个状态, 那么 \(p(x_1)\) 可以表示为含有 \(O(K)\) 个值的表 (即离散分布, 实际上根据和为 1 的约束有 \(K-1\) 个自由变量). 类似地, 条件分布 \(p(x_2\vert x_1)\) 可以表示为含有 \(O(K^2)\) 个值的二维表, 其中 \(p(x_2=j\vert x_1=i)=T_{ij}\) , 我们说 \(\mathbf{T}\) 是一个随机矩阵 (stochastic matrix), 因为它的每一行都满足 \(\sum_jT_{ij}=1\), 且每一个元素的值都满足 \(0\leq T_{ij}\leq 1\) . 类似地, \(p(x_3\vert x_1,x_2)\) 是一个有 \(O(K^3)\) 个元素的三维表. 这些表都称为条件概率表 (conditional probability tables, CPTs), 它的元素 (即模型参数) 数量随着变量的个数呈指数增长, 这对于建模来说是很差的一个选择.
1.2 条件独立
缩减参数规模的一个方法就是增加模型假设, 其中条件独立 (conditional independence, CI) 的假设最为常用.
随机变量 \(X\) 和 \(Y\) 关于 \(Z\) 条件独立, 记为 \(X\perp Y\vert Z\) , 当且仅当条件联合分布可以写为条件边际分布的乘积:
\[X\perp Y\vert Z \Longleftrightarrow p(X,Y\vert Z)=p(X\vert Z)p(Y\vert Z)\]
那么如果我们如果假设 \(x_{t+1}\perp x_{1:t-1}\vert x_t\) , 即 “给定现在, 未来与过去式独立的”. 该性质称为(一阶)马尔可夫假设 (Markov assumption) . 基于该假设和链式法则, 我们可以把联合分布写为
\[p(\x_{1:V})=p(x_1)\prod_{t=1}^Vp(x_t\vert x_{t-1})\]该模型称为(一阶)马尔可夫链 (Markov chain) . 它可以通过一个初始分布 \(p(x_1=i)\) 和一个状态转移矩阵 \(p(x_t=j\vert x_{t-1}=i)\) 来表示.
1.3 图模型
尽管一阶马尔可夫链可以表示一维随机序列的分布 (即随机过程), 但二维图像, 三维视频, 和其他高维度的数据如何表示呢? 因此这里引入图模型 (graphical model, GM) . 图模型是条件独立假设下, 联合分布的一种表示方式. 图中的节点表示随机变量, 边表示变量间的条件独立假设. 图模型有多种类别, 如有向图, 无向图, 有向和无向的结合图. 下面我们对图模型的概念做一个列举用于参考.
图 \(G=(\mathcal{V}, \mathcal{E})\) 包含一族节点 (nodes/vertices) \(\mathcal{V}=\{1,\dots,V\}\) 和一族边 (edges) \(\mathcal{E}=\{(s,t):s,t\in\mathcal{V}\}\) . 我们可以使用邻接矩阵 (adjacency matrix) 表示图, 其中 \(G(s,t)=1\) 用来表示 \((s,t)\in\mathcal{E}\) . 如果 \(G(s,t)=1\Leftrightarrow G(t,s)=1\) , 那么我们说图是无向的 (undirected) , 否则图是 有向的 (directed) , 如下图所示.
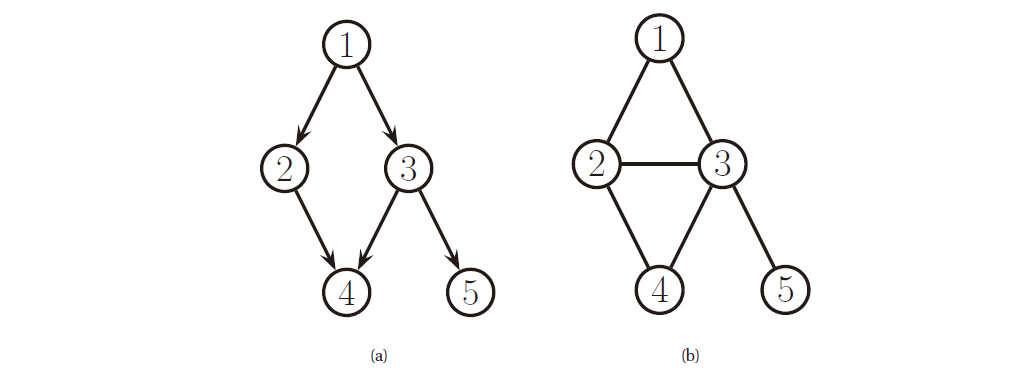
图 1. 有向图和无向图
我们通常假设 \(G(s,s)=0\) , 即没有自循环. 以下列举一下其他术语:
| 术语 | 解释 | 备注 |
|---|---|---|
| 父节点 Parent | 对于有向图, 节点的父节点是所有指向它的节点 | \(pa(s)\triangleq \{t:G(t,s)=1\}\) |
| 子节点 Child | 对于有向图, 节点的子节点是所有它指向的节点 | \(ch(s)\triangleq \{t:G(s,t)=1\}\) |
| 家族节点 Family | 对于有向图, 节点的家族节点是它和它的父节点 | \(fam(s)=\{s\}\cup pa(s)\) |
| 根节点 Root | 对于有向图, 根节点是没有父节点的节点 | |
| 叶节点 Leaf | 对于有向图, 叶节点是没有子节点的节点 | |
| 祖先节点 Ancestors | 对于有向图, 节点的祖先节点是父节点, 祖父节点等长辈节点 | \(anc(t)\triangleq\{s:s\leadsto t\}\) |
| 后代节点 Descendants | 对于有向图, 节点的后代节点是子节点, 孙子节点等晚辈节点 | \(desc(t)\triangleq\{t:s\leadsto t\}\) |
| 邻居节点 Neighbors | 对于图, 节点的邻居节点是所有与其相连的节点 | \(nbr(s)\triangleq\{t:G(s,t)=1\vee G(t,s)=1\}\) |
| 度 Degree | 对于图, 节点的度是邻居节点的个数. 有向图包含出度和入度 | |
| 圈 Cycle/Loop | 对于图, 圈是可以首位相连的一族节点. 有向图的圈称为有向圈 | \(s_1-s_2-s_3-s_1,\;1\rightarrow2\rightarrow3\rightarrow1\) |
| 有向无环图 DAG | 没有圈的有向图 | |
| 拓扑顺序 Topological ordering | 对于DAG, 拓扑顺序是节点的一种顺序编号, 使得父节点的编号小于子节点 | |
| 路径 Path/Trail | 从一个节点到另一个节点的一族有向边 | \(s\leadsto t\) |
| 树 Tree | 无向树是无向无环图, 有向树是DAG | |
| 多项树 Polytree | 允许树的节点有多个父节点 | |
| 子图 Subgraph | \(A\) 的子图是其中的部分节点和关联的边构成的图 | \(G_A=(\mathcal{V}_A,\mathcal{E}_A)\) |
| 团 Clique | 对于无向图, 团是两两互相连接的一族节点. 最大团是不能再拓展节点的团 |
1.4 有向图模型
有向图模型 (directed graphical model, DGM) 是一个基于 DAG 的图模型, 也成为贝叶斯网络 (Bayesian networks) 或 信念网络 (belief networks) . 但 DGM 和”贝叶斯”和”信念”都没什么太大关系. DAG 的主要特性就是拓扑顺序. 给定拓扑顺序, 我们给出有序马尔可夫性 (ordered Markov property) 的假设, 即节点只依赖与它的父节点, 而不依赖于父节点以外的祖先节点:
\[x_s\perp\x_{pred(s)\backslash pa(s)}\vert \x_{pa(s)}\]这是一阶马尔可夫性质从链到 DAG 的自然推广. 以前面的有向图为例, 其联合分布可以表示为:
\[\newcommand{\cancel}{\enclose{updiagonalstrike}} \begin{align}\require{enclose} p(\x_{1:5}) &= p(x_1)p(x_2\vert x_1)p(x_3\vert x_1,\cancel{x_2})p(x_4\vert \cancel{x_1},x_2,x_3)p(x_5\vert \cancel{x_1}\cancel{x_2},x_3,\cancel{x_4}) \\ &= p(x_1)p(x_2\vert x_1)p(x_3\vert x_1)p(x_4\vert x_2,x_3)p(x_5\vert x_3) \end{align}\]一般地, 我们有
\[p(\x_{1:V}\vert G)=\prod_{t=1}^Vp(x_t\vert \x_{pa(t)})\]其中每一项 \(p(x_t\vert \x_{pa(t)})\) 都是一个条件概率密度 (conditional probability distribution, CPD) . 我们把分布记为 \(p(\x\vert G)\) 是为了强调上面的等式只有在 DAG 的条件独立假设下才成立.
2. 例子
本节介绍一些常用的概率模型表示为 DGM 的例子.
2.1 朴素贝叶斯分类器
朴素贝叶斯分类器 (naive Bayes classifier) 假设在给定类别标签时特征是相互独立的, 如下图 (a) 所示.
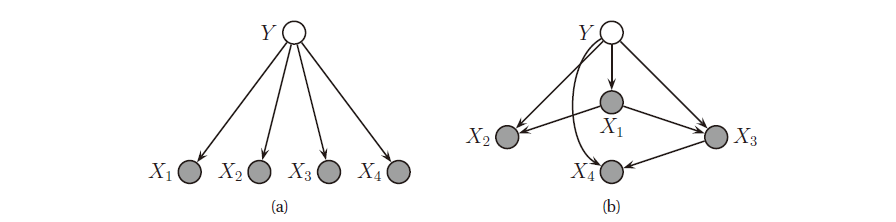
图 2. (a) 朴素贝叶斯分类器表示为 DGM, X 为观测变量, Y 为隐藏变量. (b) 树增广的朴素贝叶斯分类器
从而联合分布可以写为:
\[p(y,\x)=p(y)\prod_{j=1}^Dp(x_j\vert y)\]朴素贝叶斯分类器之所以简单, 是因为特征独立性的假设. 但如果我们希望减弱这个假设, 从而可以对特征之间进行建模, 那么可以利用 DGM. 如果模型是树, 那么这个方法就变为树增广的朴素贝叶斯分类器 (tree-augmented naive Bayes classifier, TAN) , 如上图 (b) 所示.
2.2 马尔可夫和隐马尔可夫模型
前面我们介绍过一阶马尔可夫模型. 如果当前状态依赖于前面两个节点的状态, 那么我们就得到了二阶马尔可夫模型, 如下图所示.

图 3. (a) 一阶马尔可夫链. (b) 二阶马尔可夫链
但二阶马尔可夫模型仍然难以建模链上变量的长期依赖. 另一种办法就是假设有一个潜在的随机过程, 可以通过一阶马尔可夫链建模, 而数据是该随机过程的观测值, 如下图所示. \(z_t\) 是潜变量, \(x_t\) 是观测变量. \(p(z_t\vert z_{t-1})\) 是变换模型, \(p(\x_t\vert z_t)\) 是观测模型.

图 4. 隐马尔可夫模型
2.3 医疗诊断
- ICU 中的报警网络 (alarm network)
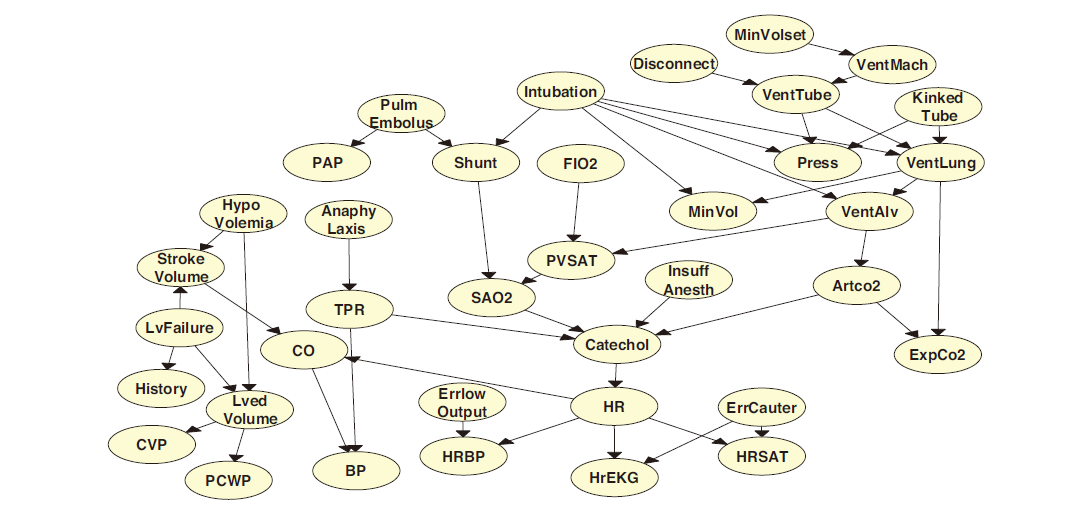
图 5. alarm network
- 诊断时的快速医疗参考 (quick medical reference)网络
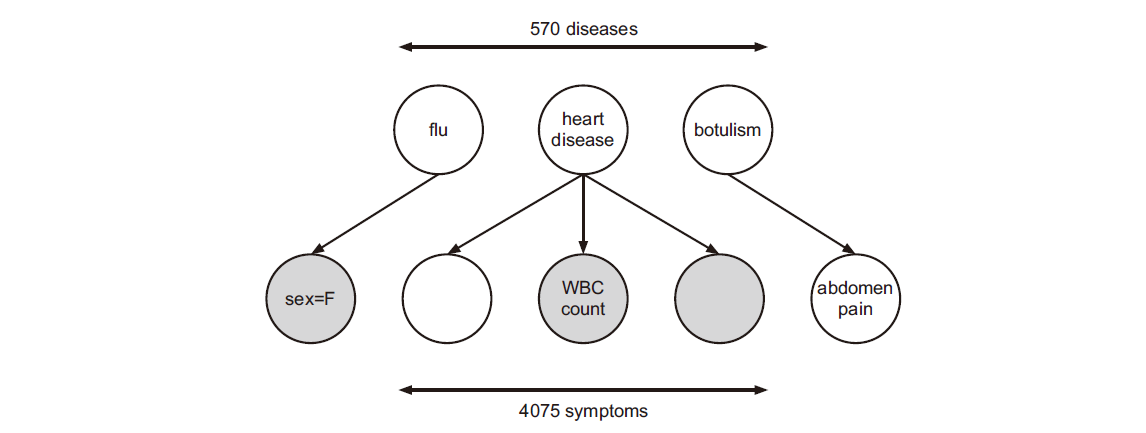
图 6. quick medical reference
详见第 10.2.3 节的内容.
3. 推断
当我们得到一个 DGM 的联合分布 \(p(\x_{1:V}\vert \tb)\) 后, 就可以用来做概率推断. 这里我们假设 \(\tb\) 已知了, 具体下一节再讨论怎么学习一个好的 \(\tb\) .
我们首先把变量分为可见变量 (visible variables) \(\x_v\) 和隐藏变量 (hidden variables) \(\x_h\) . 推断 (inference) 指的就是给定可见变量来计算隐藏变量的后验分布:
\[p(\x_h\vert \x_v,\tb)=\frac{p(\x_h,\x_v\vert \tb)}{p(\x_v\vert \tb)}=\frac{p(\x_h,\x_v\vert \tb)}{\sum_{\x_h'}p(\x_h',\x_v\vert \tb)}\]有时我们仅关心部分隐藏变量, 我们把这部分变量称为查询变量 (query variables) \(\x_q\), 而剩下的隐藏变量称为无关变量 (nuisance variables) \(\x_n\). 那么通过边缘化无关变量即可得到查询变量的计算方法:
\[p(\x_q\vert \x_v,\tb)=\sum_{\x_n}p(\x_q,\x_n\vert \x_v,\tb)\]4. 学习
学习指的是学习模型参数, 即给定数据计算模型参数的最大后验概率 (maximum a posterior, MAP) 估计:
\[\hat{\tb}=\underset{\tb}{\arg\max}\sum_{i=1}^N\log p(\x_{i,v}\vert \tb)+\log p(\tb)\]其中 \(\x_{i,v}\) 是第 \(i\) 个样本的可见变量. 如果先验是均匀分布 \(p(\tb)\propto1\) 或者数据量 \(N\) 非常大, 那么上式变成极大似然估计 (maximum likelyhood estimation, MLE) .
从完全数据 (complete data) 中学习参数是容易的, 因为上式中的似然是可以因式分解的; 但如果数据不完全, 即包含隐藏变量, 那么似然函数无法分解, 学习也变得更加困难.
5. DGMs 中的条件独立性
图模型的基础是条件独立行假设. 在图 \(G\) 中给定 \(C\) 的条件下 \(A\) 和 \(B\) 独立可以记为 \(\x_A\perp_G\x_B\vert \x_C\) . 令 \(I(G)\) 表示图 \(G\) 中所有的条件独立陈述.
我们说 \(G\) 是对于分布 \(p\) 是一个 I-map (independence map) , 或者说 \(p\) 是关于 \(G\) 的 Markov, 当且仅当 \(I(G)\subseteq I(p)\) , 其中 \(I(p)\) 是分布 \(p\) 满足的所有条件独立陈述的集合. 换句话说, 如果图模型没有对分布做任何非真的断言, 那么这个图模型就是个 I-map. 这是为了让图模型作为分布的一个安全的代理模型. 注意, 完全图的图模型一定是 I-map, 因为它包含了所有的边 (即没有对分布的独立性做任何断言).
如果 \(G\) 是 \(p\) 的一个 I-map, 并且不存在 \(G'\subseteq G\) 是 \(p\) 的 I-map, 那么我们说 \(G\) 是 \(p\) 的最小 I-map .
5.1 d-划分和贝叶斯球算法 (全局马尔可夫性)
我们首先介绍一些定义. 我们说无向路径 \(P\) 是由一族边 \(E\) (包含证据的) d-可分 (d-separated) 的, 当且仅当满足以下至少一个条件:
- \(P\) 包含一条链, \(s\rightarrow m\rightarrow t\) 或 \(s\leftarrow m\leftarrow t\) , 其中 \(m\in E\)
- \(P\) 包含一个分叉, \(s\swarrow^m\searrow t\) , 其中 \(m\in E\)
- \(P\) 包含一个 v 型结构, \(s\searrow_m\swarrow t\) , 其中 \(m\notin E\) , 并且 \(m\) 的任何后代也不属于 \(E\) .
因此, 我们说给定一族观测节点 \(E\), 一族节点 \(A\) 与另一族节点 \(B\) 是 d-可分的当且仅当从 \(a\in A\) 到 \(b\in B\) 的每一条无向路径都是在 \(E\) 下 d-可分的. 这样, 我们可以定义 DAG 的条件独立性质如下:
\[\x_A\perp_G\x_B\vert \x_E \Longleftrightarrow A \text{ is d-separated from } B \text{ given } E.\]贝叶斯球 (Bayes ball algorithm) 算法是一种简便的判断在 \(E\) 下 \(A\) 是否 d-可分于 \(B\) 的算法. 其要点在于, 我们遮住 \(E\) 中的节点, 即他们被观测到了, 我们然后把”球”放到 \(A\) 中的每一个节点处, 让他们按照一定的规则四处弹, 然后考察是否有球可以到达 \(B\) 中的节点, 规则有三条, 如下图所示:
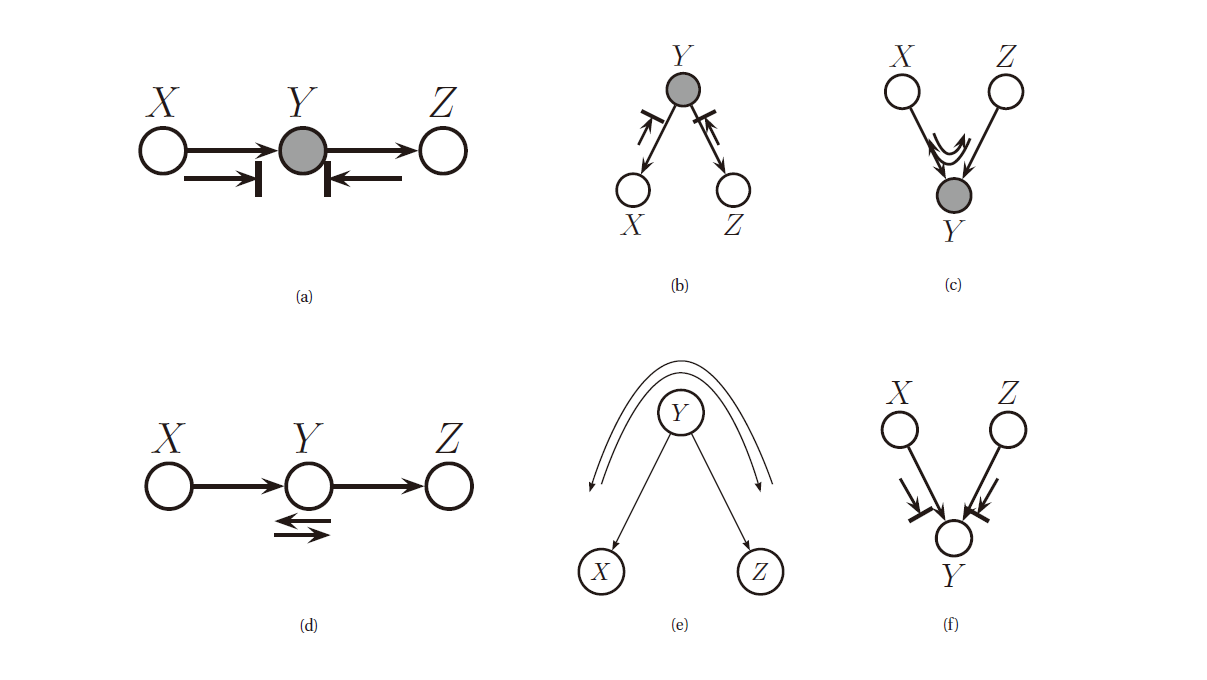
图 7. 贝叶斯球算法的三条规则 (a-c) 为存在观察变量的规则, (e-f) 为无观察变量时的规则
三条规则描述如下 (小球运动时不考虑边的方向):
- 小球可以通过一个链, 但中间存在观测变量时无法通过
- 小球可以通过分叉结构, 但中间存在观测变量时无法通过
- 小球不可以通过 V-型结构, 但中间存在观测变量时可以通过
判断这三条规则的方法如下:
5.1.1 链
考虑链式结构 \(X\rightarrow Y\rightarrow Z\) , 其联合分布如下:
\[p(x,y,z)=p(x)p(y\vert x)p(z\vert y)\]那么, 在观测到 \(y\) 时, 我们有
\[p(x,z\vert y)=\frac{p(x)p(y\vert x)p(z\vert y)}{p(y)}=\frac{p(x,y)p(z\vert y)}{p(y)}=p(x\vert y)p(z\vert y)\]因此有 \(x\perp y\vert z\) .
5.1.2 分叉
考虑分叉结构 \(X\leftarrow Y\rightarrow Z\) , 联合分布为:
\[p(x,y,z)=p(y)p(x\vert y)p(z\vert y)\]那么, 在观测到 \(y\) 时, 我们有
\[p(x,z\vert y)=\frac{p(y)p(x\vert y)p(z\vert y)}{p(y)}=p(x\vert y)p(z\vert y)\]因此有 \(x\perp y\vert z\) .
5.1.3 V-型结构
考虑 V-型结构 \(X\rightarrow Y\leftarrow Z\) , 联合分布为:
\[p(x,y,z)=p(x)p(z)p(y\vert x,z)\]那么, 在观测到 \(y\) 时, 我们有
\[p(x,z\vert y)=\frac{p(x)p(z)p(x,z\vert y)}{p(y)}\]所以 \(x\not\perp z\vert y\) . 然而, 在没有观测到 \(y\) 时, 我们有
\[p(x,z)=p(x)p(z)\]即 \(x\) 和 \(z\) 是独立的, 因此我们知道在 V-型结构下, 两个独立的变量在观测到他们的共同后代时就不再独立了. 这种现象称为 explaining away 或 inter-causal reasoning 或 Berkson’s paradox.
针对于 explaining away 的这种现象, 我们举个例子来理解. 假设我投掷了两枚硬币, 其结果用 0 和 1 表示, 那么两枚硬币的投掷结果就是随机变量 \(X\) 和 \(Z\), 两次投掷的结果之和为随机变量 \(Y\) . 那么如果我们不知道两次投掷的结果之和是多少, 那么显然两枚硬币的结果是相互独立的. 但是如果我们知道了两次投掷的和是多少, 那么两枚硬币各自的结果就耦合起来了. 比如我们预先知道和为 1, 那么第一枚硬币的观测结果就直接决定了第二枚硬币的观测结果 (即不再独立).
5.1.4 边界条件
贝叶斯球也需要边界条件, 下图 (a), (b).
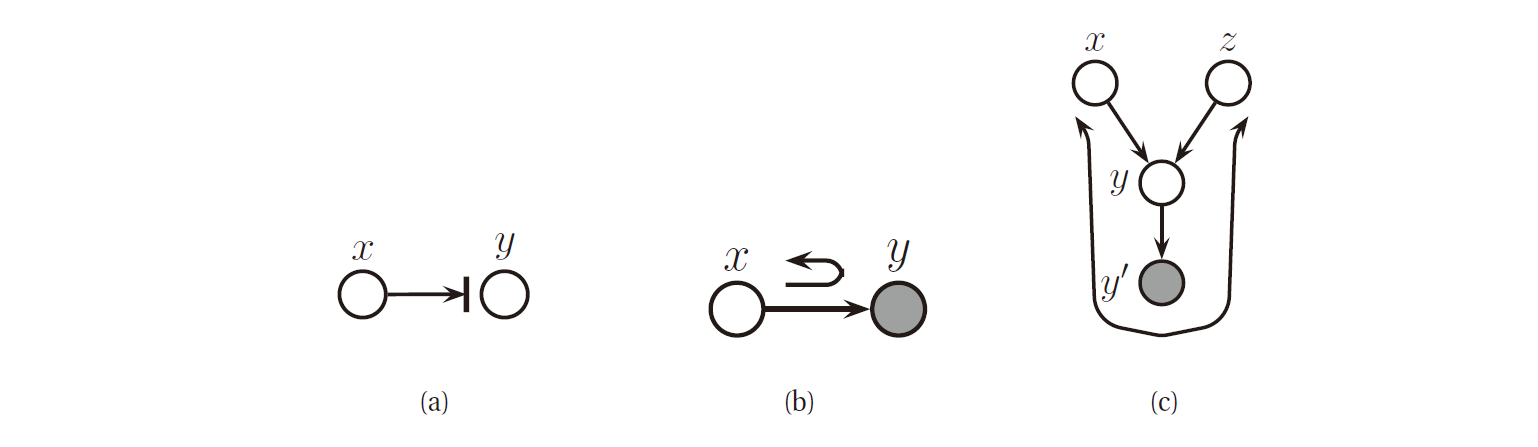
图 8. 边界条件
为了理解边界条件的含义, 如上图 (c) 所示. 假设 \(Y'\) 是 \(Y\) 的一个无噪声的副本, 那么这就意味着如果我们观测到了 \(Y'\) , 那么我们就知道了 \(Y\) , 这样两个父节点 \(X\) 和 \(Y\) 就需要耦合起来解释该观测变量. 所以, 如果我们让小球沿着 \(X\rightarrow Y\rightarrow Y'\) 的路径滚动, 它就应当沿着 \(Y'\rightarrow Y\rightarrow Z\) 的路径反弹回来. 然而, 如果 \(Y\) 和 \(Y'\) 都是隐藏变量 (即无法观测的), 那么小球就不会反弹.

图 9. DGM 的例子 (对原书的图做了修改)
比如上图.
例1: 有 \(x_2\perp x_6\vert x_5,x_1\) , 因为路径均被上述三个准则阻断:
- \(2\rightarrow5\rightarrow6\) 被 \(x_5\) 阻断 ( \(x_5\) 被观测到了)
- \(2\rightarrow4\rightarrow7\rightarrow6\) 被 \(x_7\) 阻断 ( \(x_7\) 没有被观测到)
- \(2\rightarrow1\rightarrow3\rightarrow6\) 被 \(x_1\) 阻断 ( \(x_1\) 被观测到了)
注: 这个例子在原书1中是完全错误的2, 因此这里为了给出一个正确的例子, 修改了图 (去掉了 \(3\rightarrow5\) ), 并增加了 \(x_1\) 作为观测到的变量.
例2: \(x_2\not\perp x_6\vert x_5,x_7\) , 因为 \(2\rightarrow4\rightarrow7\rightarrow6\) 没有被 \(x_7\) 阻断 ( \(x_7\) 被观测到了).
5.2 DGMs 的其他马尔可夫性质
5.2.1 有向局部马尔可夫性 L
从 d-划分的准则, 我们可以总结出有向局部马尔可夫性 (directed local Markov property):
\[t\perp nd(t)\backslash pa(t)\vert pa(t)\]其中非后代 (non-descendants) \(nd(t)=\mathcal{V}\backslash\{t\cup desc(t)\}\) . 比如上图中, 有 \(3\perp2,4\vert 1\) .
5.2.2 有序马尔可夫性 O
有序马尔科夫性 (ordered Markov property):
\[t\perp pred(t)\backslash pa(t)\vert pa(t)\]因为 \(pred(t)\subseteq nd(t)\) . 比如上图中, 有 \(5\perp 1\vert 2,3\) .
5.2.3 有向全局马尔可夫性 G
\[\x_A\perp_G\x_B\vert \x_E \Longleftrightarrow A \text{ is d-separated from } B \text{ given } E.\]显然, 我们有 \(G\Longrightarrow L\Longrightarrow O\) , 另外可以证明有 \(O\Longrightarrow L\Longrightarrow G\) , 因此这三个马尔可夫性质是等价的.
5.3 马尔可夫覆盖和全条件
使得节点 \(t\) 条件独立于图中其他所有节点的一族节点称为马尔科夫覆盖 (Markov blanket) , 记为 \(mb(t)\) . 可以证明, 马尔科夫覆盖满足:
\[mb(t)\triangleq ch(t)\cup pa(t)\cup copa(t)\]其中 \(copa(t)\) 表示协父节点 (co-parent) , 即子节点的其他父节点. 如上面图 9 中的例子, 我们有
\[mb(5)=\{6,7\}\cup\{2\}\cup\{4\}=\{2,4,6,7\}\]节点 \(t\) 的全条件表示为:
\[p(x_t\vert\x_{-t})\propto p(x_t\vert\x_{pa(t)})\prod_{s\in ch(t)}p(x_s\vert\x_{pa(s)})\]全条件在 Gibbs 采样中非常重要.
参考文献
-
Machine Learning: A Probabilistic Perspective
Kevin P. Murphy
[html], [pdf], [index], Chapter 10, Directed graphical models (Bayes nets) ↩ ↩2 -
MAJOR bug fixes/changes to appear in printing #4 (out September 2013)
[html] [index] ↩ ↩2 -
Directed Graphical Models
John Lafferty, Han Liu, and Larry Wasserman
[pdf], Chapter 18 ↩