智能剪刀(intelligent scissors)12 是一种基于图的交互式分割算法, 其机制为在两个种子点间计算最优路径, 同时移动一个种子点时可以实时更新最优路径 (根据鼠标位置实时更新路径的做法在文中称为** live wire** . 实际上智能剪刀还发展成为了后来 Photoshop 中的磁性套索 (magnetic lasso) 功能. 注: 智能剪刀只能用于二维图像.
1. 概念
我们可以把二维图像(image)看作有向图(directed graph), 像素点(pixel)作为节点(node), 相邻的像素点有边(edge)相连, 边上根据一定的规则赋以不同的权重(weight)/损失(cost)以表示从一点到边的另一点所需要的能量(energy). 由于看作了有向图, 同时考虑八联通, 那么每个像素都有指向相邻八个像素的边. 如图所示.
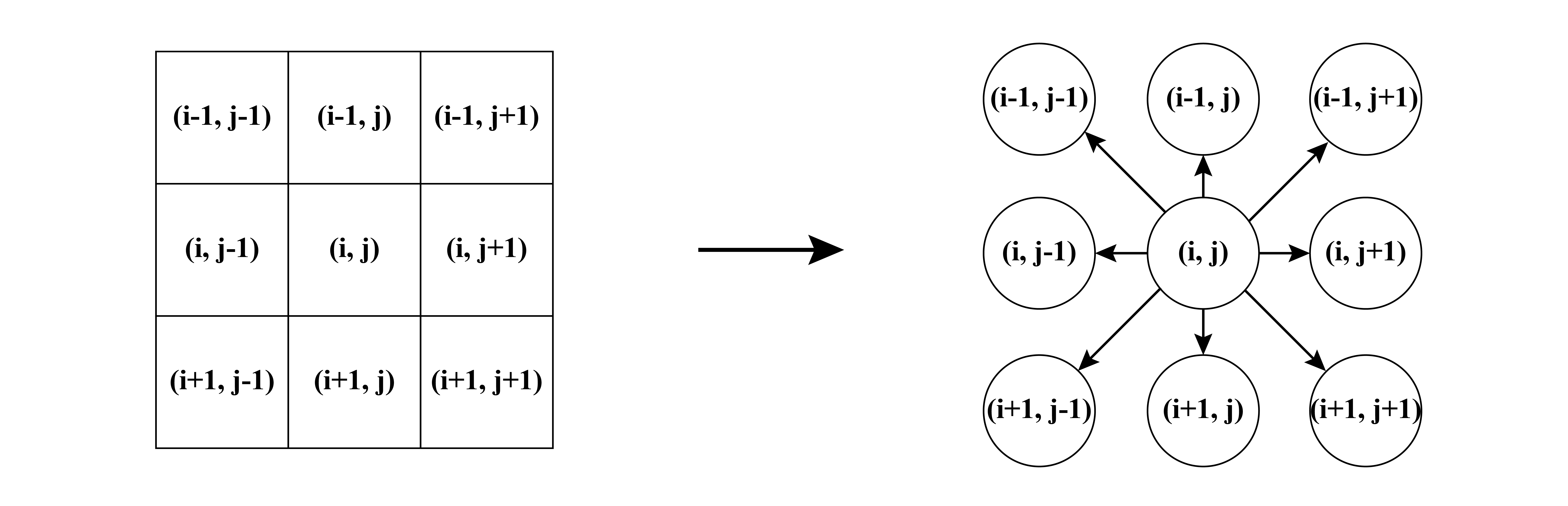
图 1. 图像 vs 图
智能剪刀的操作流程如下:
- 根据图像构造图, 包括节点和边, 使用八联通.
- 为边计算损失, 包括静态权重和动态权重.
- 用户在待分割目标的边界给定初始种子点
- 即时计算上一种子点到鼠标点间的最短路径, 移动鼠标直到用户认为最短路径恰好就是图像的边界, 点击鼠标生成下一个种子点
- 重复第4步直到目标物体的轮廓勾画完成.
2. 损失计算
计算六种损失:
| 图像特征 | 符号 | 权重 |
|---|---|---|
| Laplacian zero-crossing | \(f_Z(\mathbf{q})\) | \(w_Z\) |
| Gradient magnitude | \(f_G(\mathbf{q})\) | \(w_G\) |
| Gradient direction | \(f_D(\mathbf{p},\mathbf{q})\) | \(w_D\) |
| Edge pixel value | \(f_P(\mathbf{q})\) | \(w_P\) |
| “Inside” pixel value | \(f_I(\mathbf{q})\) | \(w_I\) |
| “Outside” pixel value | \(f_O(\mathbf{q})\) | \(w_O\) |
- 前三种为静态损失, 得到图像后可以提前计算
- 后三种为动态损失, 在交互过程中实时计算
损失(cost)的计算是很灵活的. 如最简单的根据图像强度的梯度作为损失. 本文提出的损失是六种损失的加权和. 设计损失的原则是沿着分割目标边界上的点构成的边的损失应当尽量接近0. 连接 p 和 q 两点的边总的损失如下式:
\[\begin{multline*} l(\mathbf{p},\mathbf{q}) = M\cdot(\omega_Z\cdot f_Z(\mathbf{q}) + \omega_G\cdot f_G(\mathbf{q}) + \omega_D\cdot f_D(\mathbf{p}, \mathbf{q}) \\ +\omega_P\cdot f_P(\mathbf{q}) + \omega_I\cdot f_I(\mathbf{q}) + \omega_O\cdot f_O(\mathbf{q})) \end{multline*}\]其中 M 是最大损失, 设为一个较大的常数, \(\omega_Z=0.3,\omega_G=0.3,\omega_D=0.1,\omega_P=0.1,\omega_I=0.1,\omega_I=0.1\). 拉普拉斯零交叉项 \(f_Z\) 和两个梯度损失 \(f_G, f_D\)都有静态损失函数, 可以在得到图像后预计算. \(f_G\) 和剩下的三个项都有动态损失函数(注意, \(f_G\) 既有静态损失又有动态损失), 需要在一些像素点上训练后才能得到. 因此在不训练或没有训练数据的(只有一个种子点的时候, 无法获取训练数据), 后面三项损失为 0.
2.1 Lapacian zero-crossing 拉普拉斯交叉零点
引入拉普拉斯交叉零点的主要目的是获取图像中物体轮廓的信息. 拉普拉斯算子实际上是二阶导数算子, 用于检测在图像梯度发生剧烈变化的地方. 下图展示了沿着图中红色直线上图像密度的变化, 以及相应的一阶导数和二阶导数的变化. 在图像中寻找边界, 可以从一阶导数中找极值(极大/极小值), 也可以从二阶导数中找零交叉点.
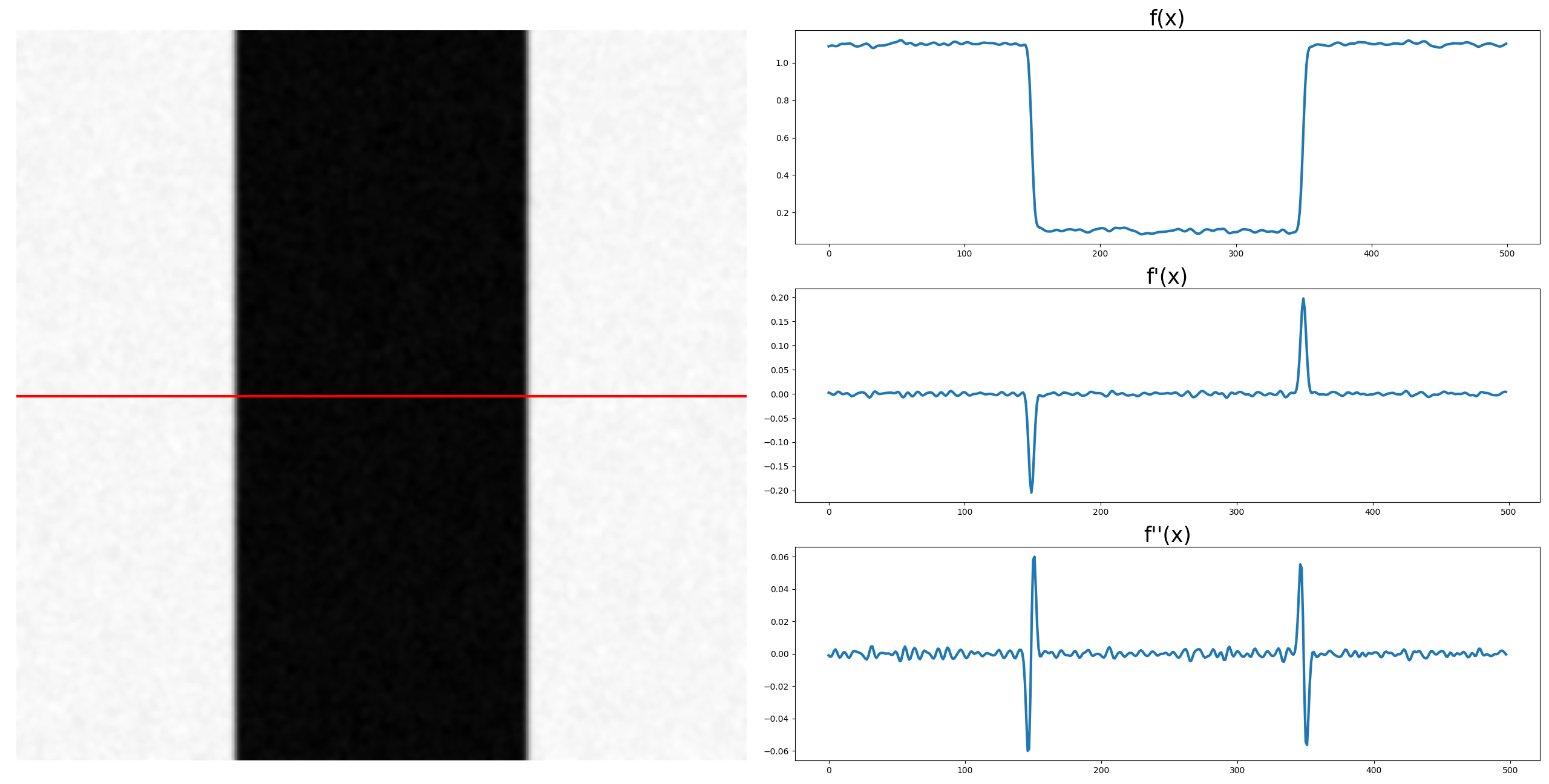
图 2. 拉普拉斯滤波器
由于拉普拉斯算子是二阶导数, 对图像中的噪声更为敏感(一阶导已经很敏感了), 因此我们先对图像做高斯滤波, 然后再应用拉普拉斯算子得到边界. 而该过程等价于把拉普拉斯算子应用于高斯函数后, 再对图像进行卷积, 从而得到基于 Laplacian of Gaussion (LoG) 滤波的方法:
\[\begin{align} G(x, y) &= \frac1{2\pi\sigma^2} \exp\left(-\frac{x^2+y^2}{2\sigma^2}\right),\\ \\ LoG(x, y) &= \Delta G(x, y) = \nabla^2G(x, y) \\ \\ &=- \frac1{\pi\sigma^4}(1-\frac{x^2+y^2}{2\sigma^2}) \exp\left(-\frac{x^2+y^2}{2\sigma^2}\right) \end{align}\]下图展示了使用 LoG 作用域图像的结果. 可以看到要得到分离性好的边界, 高斯平滑是必不可少的.

图 3. LoG 算子的效果 (某开源代码的做法)
最后我们把 LoG 的结果转化为损失函数:
\[f_Z(\mathbf{q})=\begin{cases} 0;\quad \text{if}~I_L(\mathbf{q})=0, \\ 1;\quad \text{otherwise.} \end{cases}\]在图像中, 由于像素点是离散的, 因此我们需要特别定义像素点上的零交叉点. 这里给出两种方式:
- (某开源代码的方式) 判断点 q 的八个邻接点的 LoG, 如果这八个值中既有正数, 也有负数, 那么我们认为 q 是一个零交叉点, 把 \(f_Z(\mathbf{q})\) 的值设为0, 其他为1. 这种方式的结果如上图所示.
- (论文中的方式) 判断点 q 及其相邻的下一个点 (x 和 y 方向分别做), 如果两点的 LoG 异号, 那么选择两点中绝对值小的那个作为零交叉点. 这种方式的结果如下图所示.

图 4. LoG 算子的效果 (论文的做法)
可以看到两种方式的差别在于第1种把边界上的内侧和外侧点都作为零交叉点(边界厚度为2), 第2种只把内侧和外侧点种更接近0的点作为零交叉点(边界厚度为1). 此外, 论文中使用了两种大小的高斯核: 5x5 和 9x9 的, 最终两个核分别计算 LoG, 并以 0.45 和 0.55 的权重进行加权得到最终的 fz 损失. (此处需要进一步解释.)
- 拉普拉斯零交叉损失的尺寸: [h, w], 基于点 q 的.
2.2 Gradient magnitude 梯度大小
由于拉普拉斯零交叉点是二值的, 无法区分”强”边界和”弱”边界, 因此引入梯度大小的损失项, 根据图像一阶导数计算即可:
\[G=\sqrt{I_x^2+I_y^2}.\]由于我们要根据梯度大小构造损失函数, 在边界的地方损失要小, 因此梯度大小的损失函数定义为:
\[f_G = 1 - \frac{G - \min(G)}{\max(G) - \min(G)}\]下图展示了不同大小的核得到的一阶梯度大小:
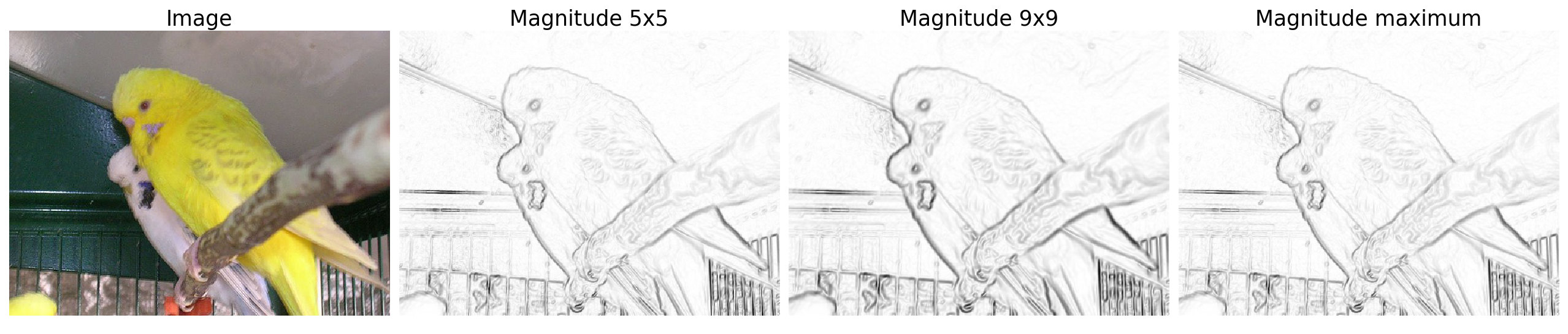
图 5. 图像梯度
考虑多核梯度大小的时候, 合并多核结果有两种策略, 这里不再使用加权, 而是取最大值:
- 对多核的梯度大小使用 maximum, 取梯度大的核对应的梯度大小, 如上图所示.
- 对多核的拉普拉斯零交叉点的斜率绝对值取 maximum. 取斜率绝对值大的核对应的梯度大小.
这里暂时不做对比, 第1种比较简单, 而且实测效果也不错.
- 梯度大小损失的尺寸: [h, w], 基于点 q 的
2.3 Gradient direction 梯度方向
梯度方向对边界增加了一个光滑性约束, 对边界方向发生突变的地方给以较大的损失. 用 \(\mathbf{D(p)}\) 表示 \(\mathbf{p}\) 点梯度的单位向量, \(\mathbf{D'(p)}\) 表示与 \(\mathbf{D(p)}\) 正交的方向(顺时针旋转90度), 即
\[\mathbf{D(p)}=[I_x(\mathbf{p}), I_y(\mathbf{p})],\quad \mathbf{D'(p)}=[I_y(\mathbf{p}), -I_x(\mathbf{p})]\]那么, 梯度方向对应的损失定义为
\[f_D(\mathbf{p},\mathbf{q}) = \frac2{3\pi} \left[ \arccos(d_\mathbf{p}(\mathbf{p},\mathbf{q})) + \arccos(d_\mathbf{q}(\mathbf{p},\mathbf{q}))\right]\]其中,
\[\begin{align} d_\mathbf{p}(\mathbf{p},\mathbf{q})) &= \mathbf{D'(p)\cdot L(p, q)} \\ d_\mathbf{q}(\mathbf{p},\mathbf{q})) &= \mathbf{L(p, q)\cdot D'(q)} \end{align}\]其中,
\[L(p,q)=\frac1{\Vert\mathbf{p-q}\Vert} \begin{cases} \mathbf{q-p};\quad \text{if}~~\mathbf{D'(p)\cdot(q-p)}\geq0 \\ \mathbf{p-q};\quad \text{otherwise} \end{cases}\]是个单位向量. 注意到反余弦 arccos 是 [-1, 1] 上单调递减的函数, 该损失函数定义的方式使得:
- 边的两个端点的梯度方向一致并且与边的方向也一致时损失较低
- 边的两个端点的梯度方向一致但与边的方向正交时损失较高
- 边的两个端点的梯度方向不一致时损失较高
如下图所示. 图中有个笔误, 第三幅图的 dq(p, q) = -0.957.

图 6. 梯度方向损失的计算
- 梯度方向损失的尺寸: [3, 3, h, w], 基于边 p–q 的
- 以上三个损失中, 前两个损失需要统一做一个 unfold 的操作, 把 [h, w] 的尺寸变为(复制为) [3, 3, h, w], 最终得到一个四维张量 i,j,k,l, 其中 k 和 l 维度指代像素 p 的绝对坐标, 而 i 和 j 指代像素 p 的邻居 q 在 3x3 的小网格内的坐标.
2.4 Pixel value features 像素值特征
在用户勾画的过程中, 已经完成的边界对于后续边界的识别是更有意义的, 因此文章提出了利用先前的边界段对图中边的权重进行调整(或者说训练), 从而 live wire 更加”跟手”.
像素值特征只有在训练过后才有意义. 边像素值 (edge pixel values) 损失是用于训练的边界下对应的像素值, 乘上一个缩放因子. 对于自然图像, 有:
\[f_P(\mathbf{p})=\frac1{255}I(\mathbf{p})\]内部和外部像素值(“inside” and “outside” pixel values) 损失所取的点是沿着梯度方向一定距离的地方采样的:
\[f_I(\mathbf{p})=\frac1{255}I(\mathbf{p}+k\cdot\mathbf{D(p)}) \\ f_O(\mathbf{p})=\frac1{255}I(\mathbf{p}-k\cdot\mathbf{D(p)})\]为什么需要动态训练边的权重呢?
- 因为有些图像中, 梯度”强”的边未必是用户需要的边, 而”强”边附近的”弱”边可能是需要的. 在2.1-2.3中的三个静态损失下, 弱边是没有发言权的. 比如论文中的下图.
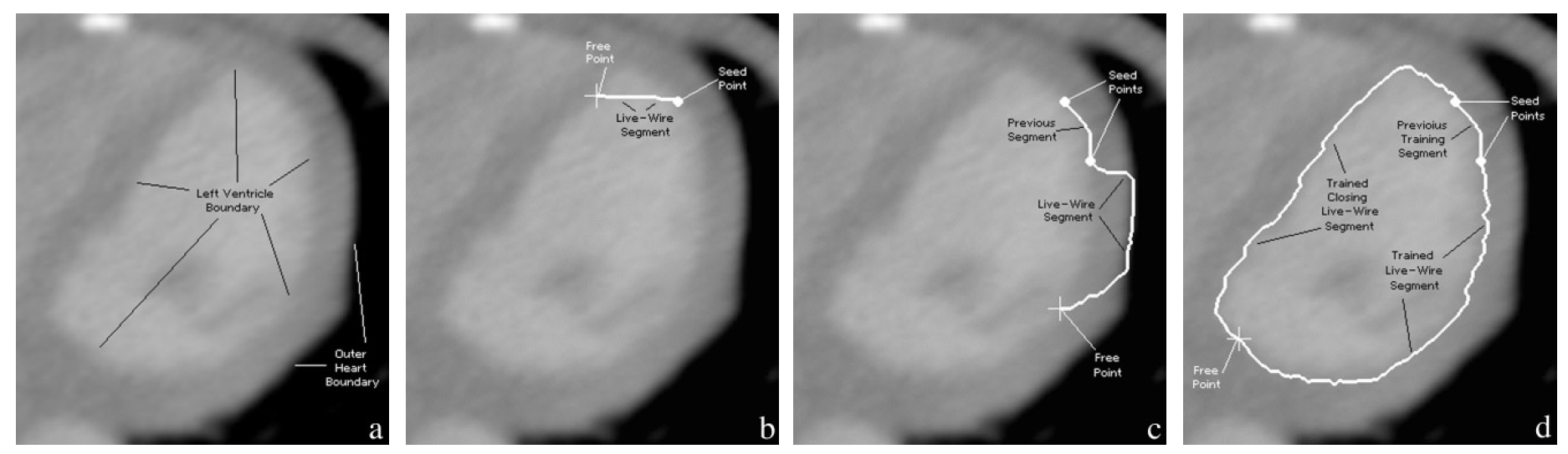
图 7. 心脏 CT 的例子
以上三个基于像素值的损失和梯度大小的损失都是可以动态计算的, 要根据用于训练的一段边界上的像素点, 计算直方图 \($h_G\)$. 由于点不多( t=32/64 个像素点), 因此计算出来的直方图可能噪声比较多, 因此对直方图应用一维高斯平滑来抑制噪声. 然后对直方图进行归一化并取补, 从而满足边界点的损失低的要求:
\[m_G=\left\lfloor M_G\left(1 - \frac{h_G}{\max(h_G)}\right)+0.5\right\rfloor\]其中 round 为四舍五入取整的函数, \(M_G = \omega_G\cdot M\), 类似地可以求出 \(m_P, m_I, m_O\).
当获取到的样本点太少的时候(给定阈值 s 和最大样本点数量 t ), 梯度大小的动态损失是不靠谱的, 甚至会起到反作用, 因此当样本点的数量 \(t_s\) 少于 s 的时候, 我们认为动态损失不靠谱, 需要额外调整; 样本点多于 s 的时候, 我们认为动态损失还比较靠谱, 不再调整:
其中 \(n_G=1024\) (这个 1024 也不知道怎么来的…), \(x=0,1,\dots,n_G-1\) 为 \(m'_G\)的支撑, 即直方图取值的 bins. 对于上式的理解, 可以分为两部分:
- 当用于训练的样本点的数量 \(t_s\) 足够大时 (超过 s ), 那么我们认为 \(m_G\) 作为梯度大小的直方图是可靠的, 因此可以用作梯度大小的损失函数.
- 当没有训练样本的时候, 我们使用 2.2 节的 \(f_G\) 作为梯度大小的损失.
- 当 \(t_s\) 不够大时 (小于 s ), 对于 \(m_G\) 的信任就要打一个折扣, 那么实际的损失函数则使用情况1和情况2的组合
三种情况如下图所示. 第一列是 \(m_G(x)\), 第二列是上面公式中min函数内的第二项, 第三列是 min 函数的结果. (注意 \(t_s\) 是样本点的数量, 不同的 \(t_s\) 对应的第一列 \(m_G(x)\) 实际上是不同的, 要根据实际的点计算直方图, 这里是偷懒用了同一幅图来表示了).
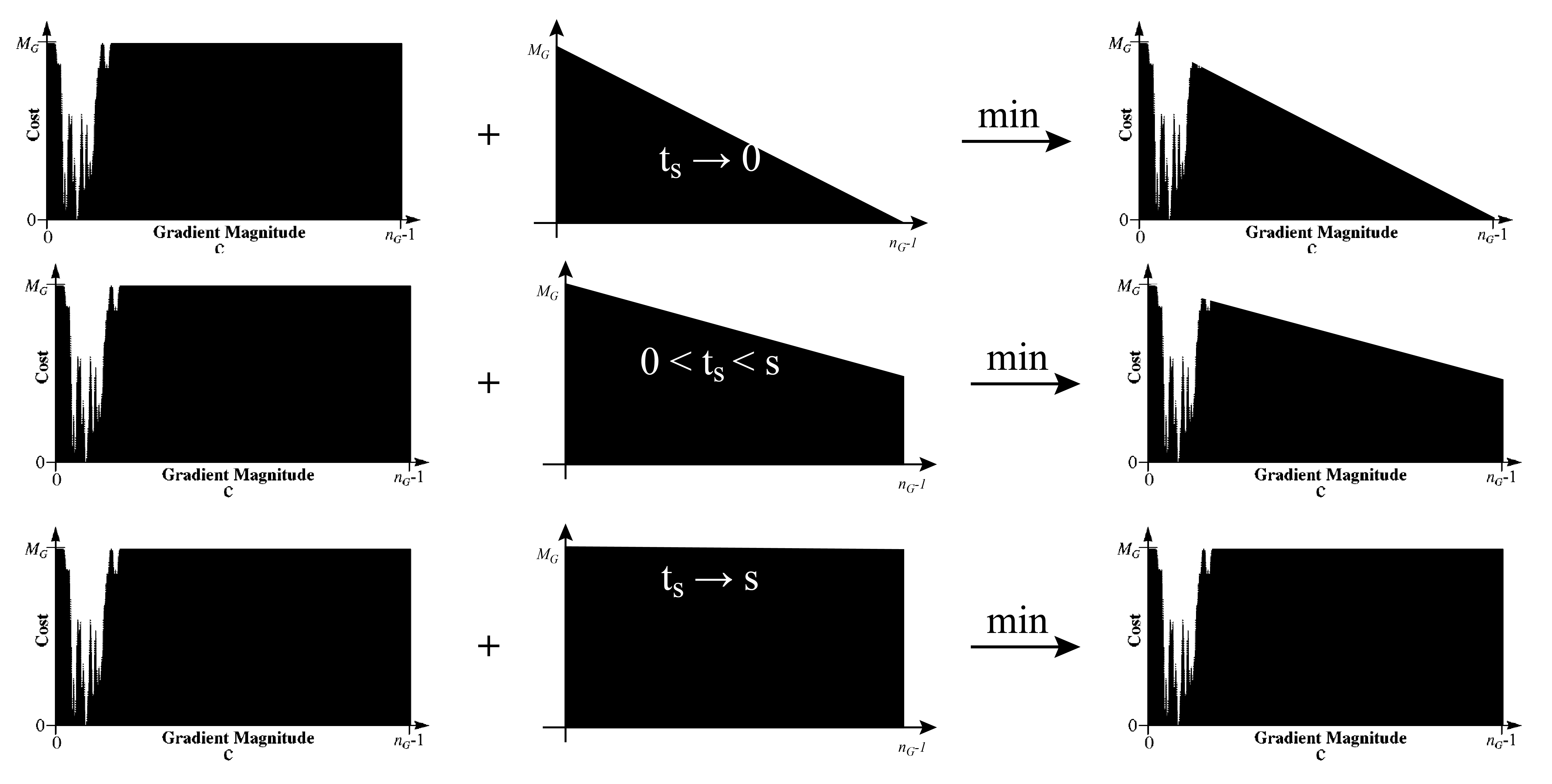
图 8. 梯度大小的动态损失
此外, 对于梯度大小损失, 由于水平垂直的邻点和斜对角的邻点到中心的 p 点的距离是不同的, 因此梯度大小损失需要额外乘一个常数项:
\[w_N(\mathbf{p}, \mathbf{q})=\begin{cases} 1; \quad &\mathbf{q}~\text{is a diagonal neighbor}, \\ 1/\sqrt{2};\quad &\mathbf{q}~\text{is a horizontal or vertical neighbor}. \end{cases}\]2.5 最终损失
综上, 总的损失由两个静态损失(拉普拉斯零交叉, 梯度方向), 一个静态+动态损失(梯度大小), 三个动态损失(边/内/外像素值)构成. (一个猜测: 由于这两篇文章是95年/98年的, 当时电脑的性能还挺差, 所以作者为了提高计算效率, 最终把所有损失都放大了 M 倍, 并近似为整数), 损失函数最终变为:
\[\begin{multline*} l'(\mathbf{p},\mathbf{q})=\lfloor M_Z\cdot f_Z(\mathbf{q})+0.5\rfloor + \lfloor M_D\cdot f_D(\mathbf{p},\mathbf{q})+0.5\rfloor \\ +w_N(\mathbf{p},\mathbf{q})\cdot m'_G(I_G(\mathbf{q})) +m_P(I_P(\mathbf{q})) +m_I(I_I(\mathbf{q})) +m_O(I_O(\mathbf{q})). \end{multline*}\]其中 \(M_Z=\omega_Z\cdot M, \; M_D=\omega_D\cdot M\).
3. 实际操作和最短路径的计算
在第2节我们详细讨论了边权的计算, 最后我们需要根据用户交互的种子点计算最短路径. 过程如下:
- 计算两个静态损失, 和梯度大小的静态损失部分
- 用户给定第一个种子点
- 以种子点为中心, 提取图像的一个 NxN 的 patch, 在该 patch 上进行后续计算, 以减少计算量. (相当于 live wire 只在该种子点为中心边长为 N 的一个矩形区域内有效. 当然了图像不大或者算力足够时可以直接用全图计算.)
- 在计算区域内使用 Dijkstra 单源最短路径算法计算所有像素点到刚点的种子点的最短路径
- 根据鼠标位置实时更新当前的 live wire
- 用户根据 live wire 确定一条最优路径, 点击鼠标生成下一个种子点, 则第一个种子点和下一个种子点之间的路径就完全确定.
- 从前一步确定的路径末尾提取32/64个像素点作为训练集, 计算三个动态损失, 并更新图的权重 (注意要基于第1步的权重更新, 只对当前 live wire 有效. )
- 返回第4步
4. 参考文献
-
Interactive segmentation with intelligent scissors
Mortensen E N, Barrett W A.
[html], [PDF]. In Graphical models and image processing, 1998, 60(5): 349-384. ↩ -
Intelligent scissors for image composition
Mortensen E N, Barrett W A.
[html], [PDF]. In Proceedings of the 22nd annual conference on Computer graphics and interactive techniques. 1995: 191-198. ↩