1. TADAM1: Task dependent adaptive metric
本文提出了 metric scaling 和 metric task conditioning 来优化少样本学习的性能.
1.1 Metric Scaling
通常在 FSL 中, 分类器定义如下:
\[p_{\phi}(y=k\vert x) = \text{softmax}(-d(\mathbf{z}, \mathbf{c}_k)),\]其中 \(z\) 是查询样本的特征, \(\mathbf{c}_k\) 是第 \(k\) 个类别上支撑样本的特征, \(d\) 是一个距离函数, 通常用欧氏距离或余弦距离. 本文提出的 metric scaling 就是对 \(d\) 进行一个缩放, 如下式:
\[p_{\phi, \alpha}(y=k\vert x) = \text{softmax}(-\alpha d(\mathbf{z}, \mathbf{c}_k)),\]其中 \(\alpha\) 是一个可学习的参数. 在 multi-shot 的情形下有一个点的精度提升, one-shot 略有提升. 文章对 \(\alpha\) 的作用进行了详细的分析. 首先给出第 \(k\) 个类别的交叉熵损失:
\[J_k(\phi, \alpha) = \sum_{x_i\in \mathcal{Q}_k,} \left[ \alpha d(\mathbf{z}, \mathbf{c}_k) + \log\sum_j\exp(-\alpha d(\mathbf{z}, \mathbf{c}_j)) \right], \quad z=f_{\phi}(x_i),\]其中 \(\mathcal{Q}_k,=\{ (x_i, y_i)\in Q \vert y_i=k \}\) 是查询集中第 \(k\) 个类别的集合. 损失函数 \(J_k\) 的梯度为:
\[\frac{\partial}{\partial\phi}J_k(\phi, \alpha) = \alpha\sum_{x_i\in \mathcal{Q}_k,}\left[ \frac{\partial}{\partial\phi}d(\mathbf{z}, \mathbf{c}_k) - \frac{\sum_j\exp(-\alpha d(\mathbf{z}, \mathbf{c}_j))\frac{\partial}{\partial\phi}d(\mathbf{z}, \mathbf{c}_j)}{\sum_j\exp(-\alpha d(\mathbf{z}, \mathbf{c}_j))} \right].\]首先, \(\alpha\) 是对整体梯度的一个缩放因子. 其次, \(\alpha\) 是指数内的一个平滑因子. 文章主要分析了 \(\alpha\) 趋于 \(0\) 和 \(\infty\) 的情况下梯度变化的趋势.
引理 如果如下假设成立的话:
\[\mathcal{A}_1:\; d(f_{\phi}(x), \mathbf{c}_k) \neq d(f_{\phi}(x'), \mathbf{c}_k), \forall k, x\neq x'\in \mathcal{Q}_k,; \quad \mathcal{A}_2:\; \left\vert \frac{\partial}{\partial\phi}d(f_{\phi}(x), c) \right\vert<\infty, \forall x, c, \phi,\]那么, 下列等式成立
\[\begin{align} \lim_{\alpha\rightarrow0}\frac1{\alpha}\frac{\partial}{\partial\phi}J_k(\phi, \alpha) &= \sum_{x_i\in \mathcal{Q}_k,} \left[ \frac{K-1}{K}\frac{\partial}{\partial\phi}d(\mathbf{z}, \mathbf{c}_k) - \frac1K\sum_{j\neq k}\frac{\partial}{\partial\phi}d(\mathbf{z}, \mathbf{c}_j) \right], \\ \lim_{\alpha\rightarrow\infty}\frac1{\alpha}\frac{\partial}{\partial\phi}J_k(\phi, \alpha) &= \sum_{x_i\in \mathcal{Q}_k,} \left[ \frac{\partial}{\partial\phi}d(\mathbf{z}, \mathbf{c}_k) - \frac{\partial}{\partial\phi}d(\mathbf{z}, c_{j^*_i}) \right]; \end{align}\]其中 \(j^*_i=\arg\min_j d(\mathbf{z}, \mathbf{c}_j)\).
第一个公式是 trivial 的, 第二个公式的证明过程如下.

图 1. 第二个公式的证明
-
当 \(\alpha\) 很小时, 第一个式子右侧第一项是使得极小化了查询样本 \(z\) 和对应类别的原型 \(\mathbf{c}_k\) 之间的距离, 第二项极大化了 \(z\) 和不同类别原型之间的距离.
-
当 \(\alpha\) 很大时, 第二个式子右侧第一项一样, 第二项极大化 \(z\) 和离 \(z\) 最近的不同类别原型之间的距离 (有点 maxmin 的感觉). 如果 \(j^*_i=k\), 则第二个式子值为 \(0\). 这表明在 \(\alpha\) 很大时, 模型主要从困难样本中学习 (maxmin 的体现).
1.2 Task Conditioning
进行特征调整 (feature modulation), 引入一组 \(\gamma\) 和 \(\beta\) 参数对主干网络进行 task-specific 的调整, 从而把 task-agnostic 的主干网络变为 task-related 的主干网络. 老规矩, 插入 BN 层之后. 本文构造了个 task embedding network (TEN) 来生成 task-specific 的 \(\gamma\) 和 \(\beta\), 结构如下.
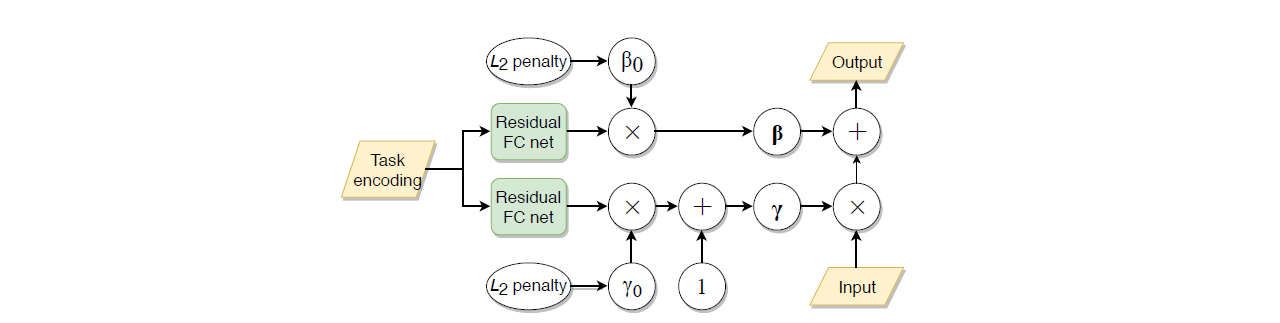
图 2. TEN 的结构
首先用一个网络提取支撑集样本的特征, 通过 Residual-FC 网络编码为相应的 task-related 的特征, 引入两个可学习的参数 \(\gamma_0\) 和 \(\beta_0\) 控制该层 TEN 模块的起作用程度. \(\gamma\) 后面加了个 \(1\), 表明 \(\gamma\) 学习的是增量, 有利于稳定训练. 由于支撑集特征需要先提取出来, 才能返回去嵌入网络, 因此最终模型训练包含一个循环结构, 如下图所示.
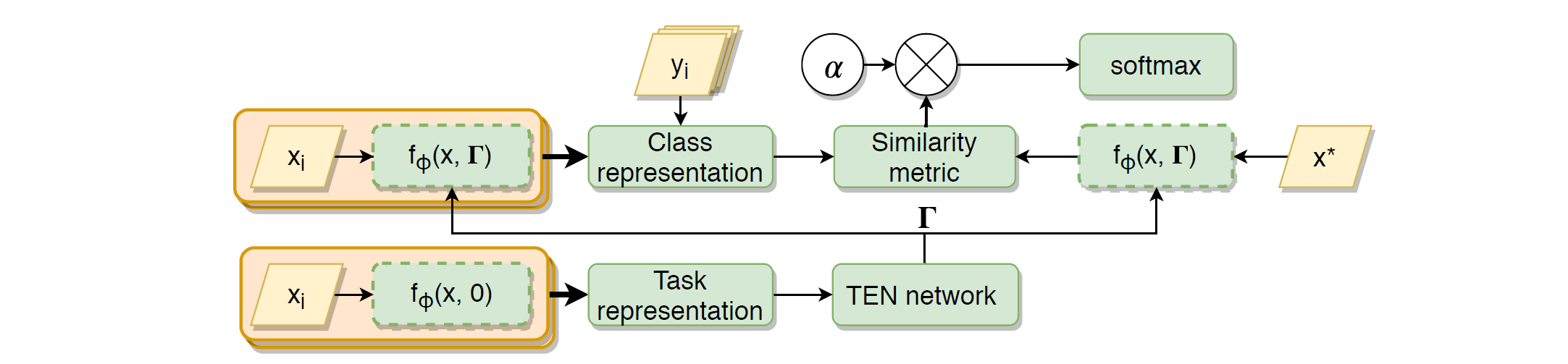
图 3. 本文提出的用于 FSL 网络结构
然而, 通常来说网络中包含大规模循环结构的基本都训练不成, 或者精度反而下降了 (包含小循环的 RNN 都很难训练). 因此本文还得再对模型做一点修改: 加一个辅助的分类任务, 并应用退火的手段逐渐减弱辅助训练的影响, 最后才训练成功. 与其他方法的对比结果如下表.
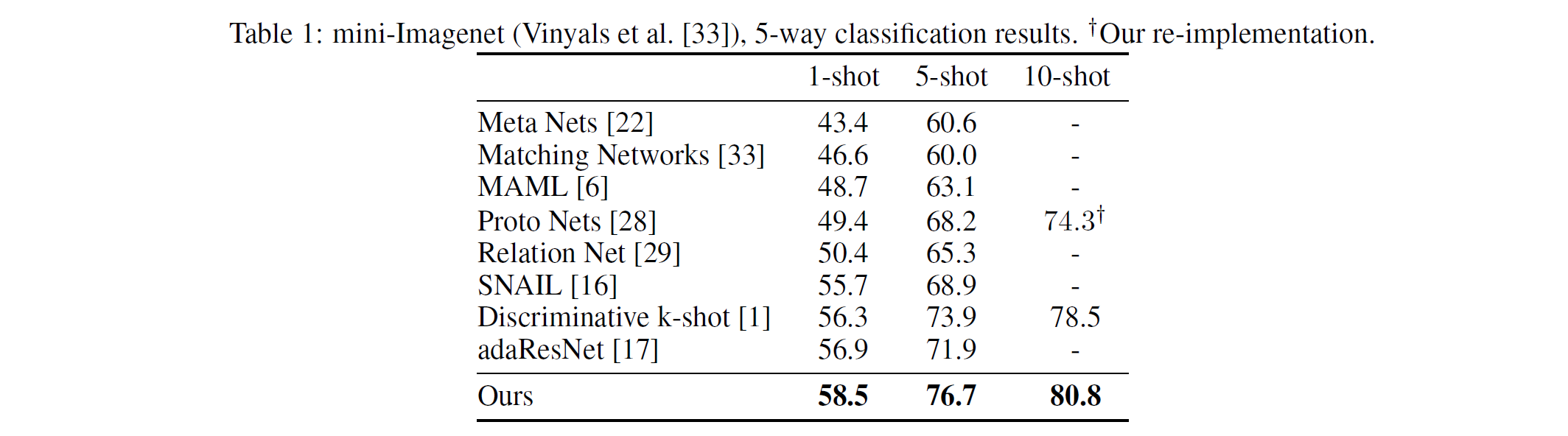
图 4. 本文的结果与其他方法的比较
消融实验如下.
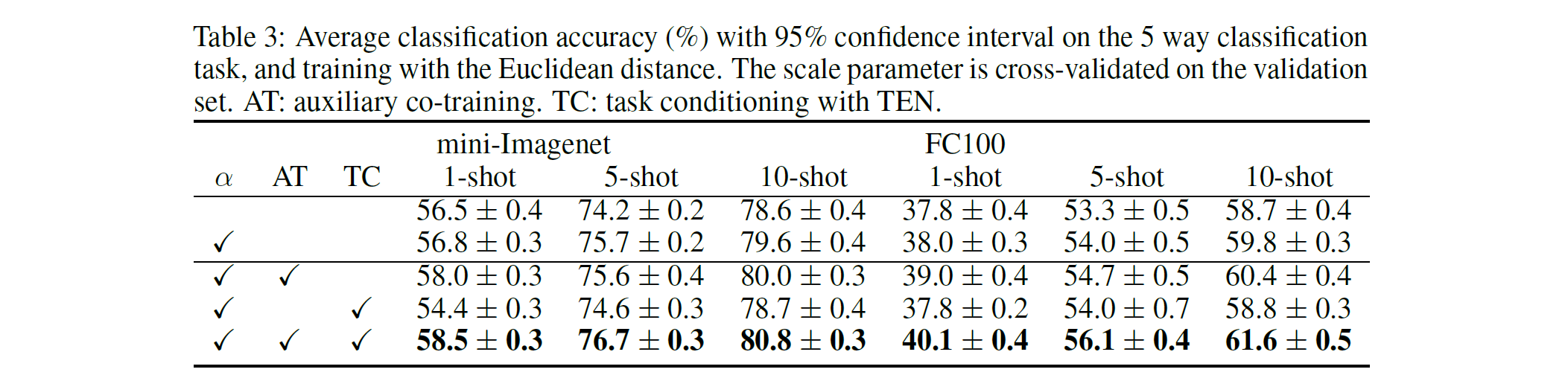
图 5. 消融实验