1. TapNet1: Task-Adaptive Projection
TapNet 提出了一种 task-adaptive projection 用于少样本学习. 嵌入空间的特征以一种任务相关的形式线性映射到一个新的空间以提升分类准确率. query 特征不再直接和 support 特征比较, 而是和这个新的投影空间中的参考向量 (reference vector) 比较.
1. 模型
在少样本学习中(这里考虑分类任务), 对于 \(N_c\)-way 1-shot 的任务, 一个 episode 包含一族支撑集
\[\{(x_1, y_1), \cdots, (x_{N_c}, y_{N_c})\}\]和一族查询集
\[\{ (\hat{x}_1, \hat{y}_1), \cdots, (\hat{x}_{N_c}, \hat{y}_{N_c}) \} .\]TapNet 包含三个部分, 特征提取网络 \(f_{\theta}\), 一族类别相关的向量 \(\Phi\) 和 task-specific 的自适应的映射 \(M\) 用于进行特征映射. 其中 \(\Phi=[\phi_1;\phi_2,\cdots;\phi_{N_c}]\) 是一个矩阵, 其中的每一行都是一个类别相关的参考向量 \(\phi_k\) (默认都是行向量), 这个矩阵是参数化的, 即其中的值是通过反向传播来学习的.
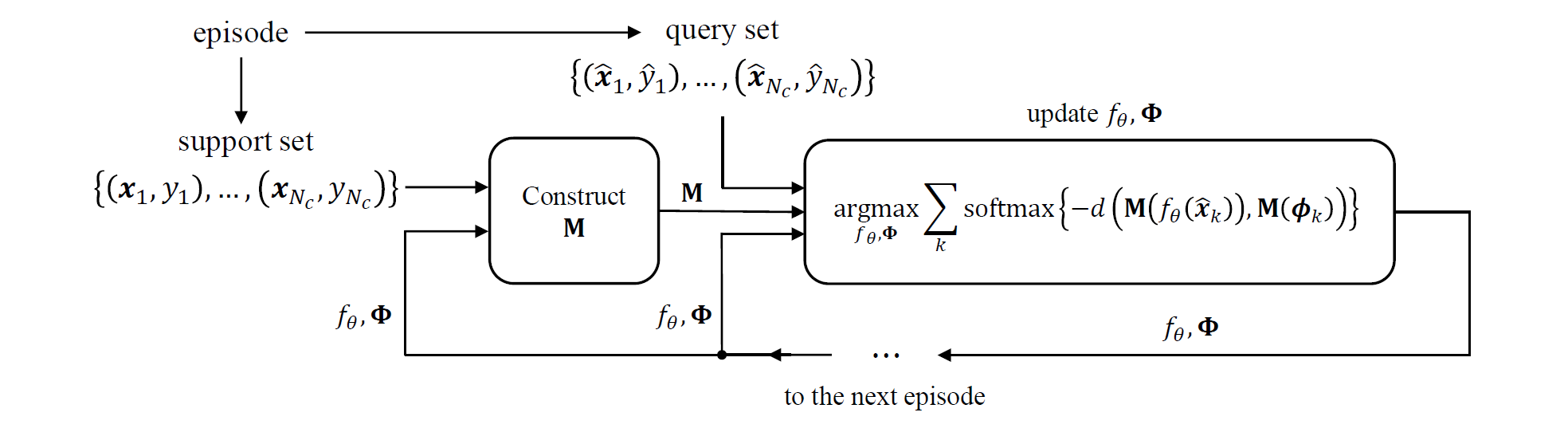
图 1. TapNet 结构示意图
模型结构如上图所示. 给定一个新的 episode, 对于上一步训练后的 \(f_{\theta}\) 和 \(\Phi\), 首先构造映射矩阵 \(M\) (体现了 task-specific), 要使得原始嵌入空间的特征 \(f_{\theta}(x_k)\) 和参考向量非常接近. 然后把查询向量和参考向量在映射空间中的欧氏距离作为优化目标, 在欧氏距离上使用 softmax 函数进行标准化, 如下式所示.
\[softmax\left( -d(M(f_{\theta}(\hat{x}_k)), M(\phi_k)) \right) = \frac{exp\left( -d(M(f_{\theta}(\hat{x}_k)), M(\phi_k)) \right)}{\sum_l\exp\left( -d(M(f_{\theta}(\hat{x}_k)), M(\phi_l)) \right)}\]在 few-shot 测试阶段, 首先构造 \(M\), 把特征映射到另一个空间, 然后在映射空间中进行分类.
2. Tap 空间的构造
Task-Adaptive Projection 空间 (Tap 空间) \(M\) 的构造方式为: 通过 \(M\) 对齐支撑集特征和参考向量. 令 \(c_k\) 表示第 k 个类别的支撑集特征的平均. 我们希望
- 通过 \(M\) 来对齐 \(c_k\) 和 \(\phi_k\), 同时我们希望
- \(c_k\) 和 \(\phi_l, l\neq k\) 在该空间中尽量分离.
因此本文提出了如下的方法, 通过对齐 \(c_k\) 和一个衍生的向量 \(\tilde{\phi}_k\):
\[\tilde{\phi}_k = \phi_k - \frac1{N_c - 1}\sum_{l\neq k}\phi_l,\]其中因子 \(1/(N_c - 1)\) 可以看作一个标准化系数. 那么为了满足1, 2两点, 只需要寻找 \(M\), 使得对于每一个 \(k\), 误差向量
\[\epsilon_k = \frac{\tilde{\phi}_k}{\Vert \tilde{\phi}_k \Vert} - \frac{c_k}{\Vert c_k \Vert}\]在 \(M\) 空间中为零即可. 那么满足此条件的 \(M\), 其列向量张成的空间即为我们寻找的 Tap 空间. 换句话说, 我们要找的就是误差向量 \(\epsilon_k\) 的零空间, 表示为:
\[M = null_D([\epsilon_1; \cdots; \epsilon_{N_c}]),\]其中 \(D\) 是 \(M\) 的列数. 求矩阵 \([\epsilon_1; \cdots; \epsilon_{N_c}]\) 零空间的一种方法是 SVD 分解, 取 \(V\) 矩阵的第 \(N_c + 1\) 到 \(N_c + D\) 的 \(D\) 个奇异向量. 令 \(L\) 为嵌入空间特征的长度, 那么只要 \(L\leq N_c + D\), 那么 \(D\) 维的投影空间 \(M\) 总是存在的.
算法流程如下.

图 2. TapNet 算法流程
3. 分析
与 Matching Networks 和 Prototypical Networks 的对比:
- Matching Networks: \(d(f_{\theta}(\hat{x}_k), g_{\phi}(x_k))\)
- Prototypical Networks: \(d(f_{\theta}(\hat{x}_k), f_{\theta}(x_k))\)
- TapNets: \(d(M(f_{\theta}(\hat{x}_k)), M(\phi_k))\)
结果如下图.
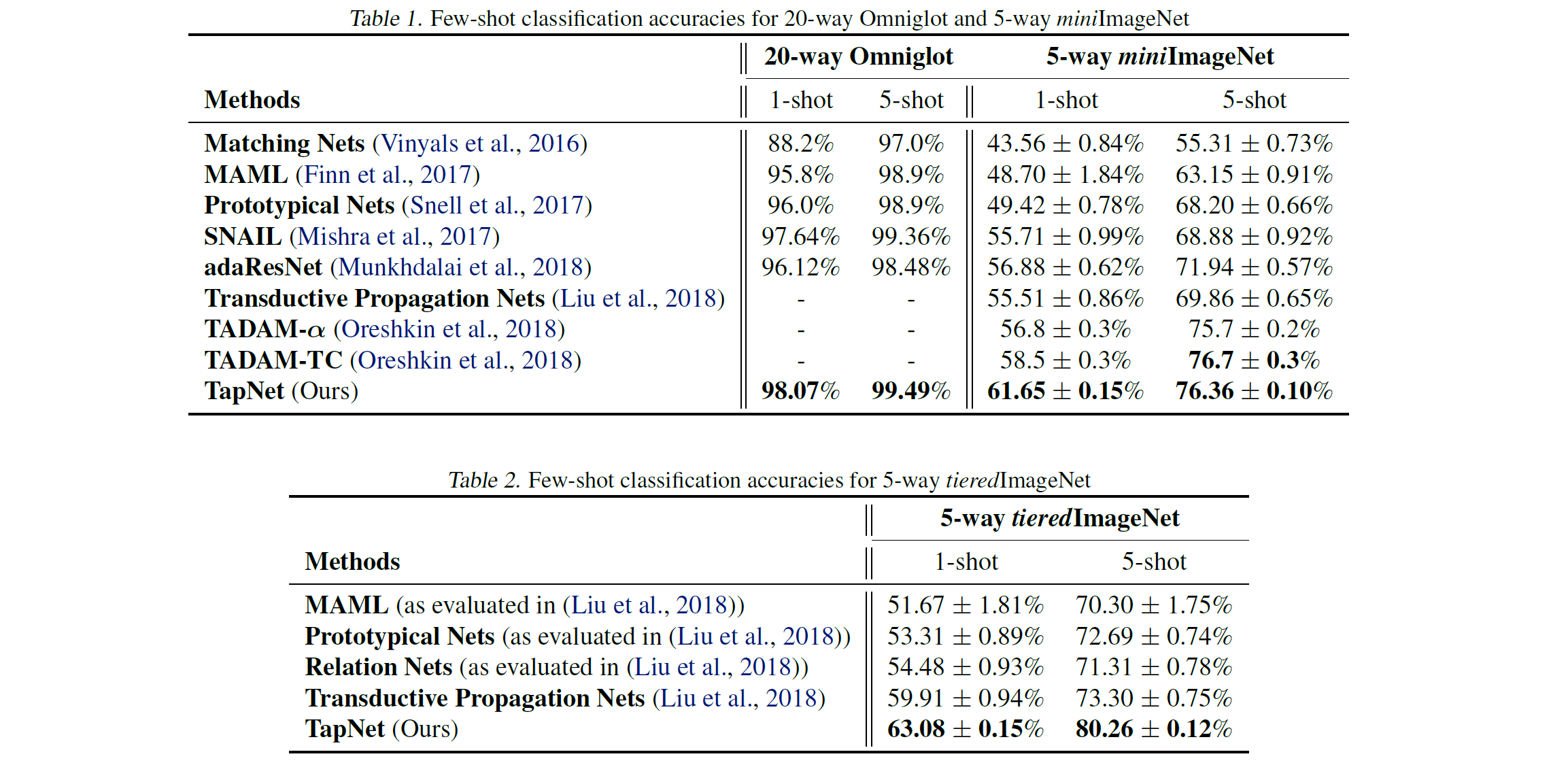
图 3. TapNet 实验结果