本文记录一些遇到的有关正态分布的计算和结论.
正态分布的形式, 正态分布的 KL 散度, 正态分布随机变量的和, 重参数化技巧
正态分布的形式
正态分布 (也叫高斯分布), 是一种连续变量的实值随机变量的分布.
一元正态分布
一元正态分布的概率密度函数 (probability density function, PDF) \(\mathcal{N}(\mu, \sigma^2)\) 如下:
\[f(x) = \frac1{\sigma\sqrt{2\pi}} e^{-\frac12\left(\frac{x-\mu}{\sigma}\right)^2}\]其中 \(\mu\) 和 \(\sigma^2\) 分别是正态分布的均值 (mean) 和方差 (variance). 正态分布的累积分布函数 (cumulative distribution function, CDF) 如下:
\[\Phi(x) = \frac1{\sigma\sqrt{2\pi}} \int_{-\infty}^x e^{-\frac12\left(\frac{x-\mu}{\sigma}\right)^2}\,dt\]正态分布的概率密度函数如下图:
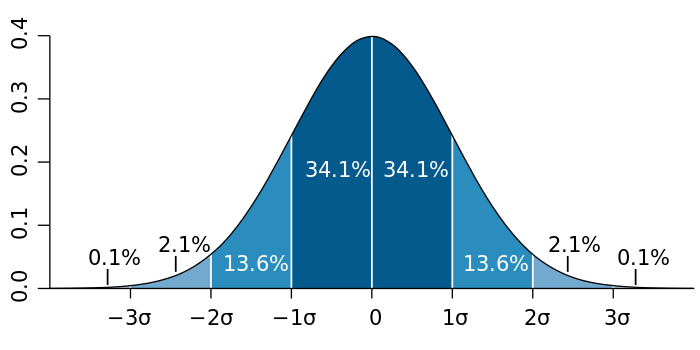
图 1. 正态分布的概率密度函数
多元正态分布
多元正态分布 (multivariate normal distribution) \(\mathcal{N}(\pmb{\mu}, \pmb{\Sigma})\) 的 PDF 为:
\[f_{\pmb{X}}(x_1,\dots,x_k) = \frac1{(2\pi)^{n/2}\vert\pmb{\Sigma}\vert^{1/2}}\exp\left(-\frac12(\pmb{x}-\pmb{\mu})^T\pmb{\Sigma}^{-1}(\pmb{x}-\pmb{\mu})\right)\]其中 \(\pmb{\mu}\) 和 \(\pmb{\Sigma}\) 是均值向量和协方差矩阵.
二元正态分布的概率密度函数如下图:
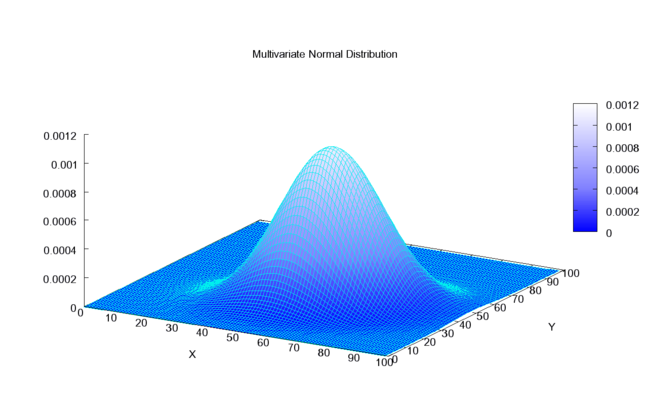
图 2. 二元正态分布的概率密度函数
正态分布的 KL 散度
两个正态分布的 KL 散度为:
\[D(P_1\Vert P_2) = \frac12\left(\log\frac{\vert\pmb{\Sigma}_2\vert}{\vert\pmb{\Sigma}_1\vert} - n + \text{tr}(\pmb{\Sigma}_2^{-1}\pmb{\Sigma}_1) + (\pmb{\mu}_2-\pmb{\mu}_1)^T\pmb{\Sigma}_2^{-1}(\pmb{\mu}_2-\pmb{\mu}_1)\right)\]推导过程如下. 根据两个分布 \(P\) 和 \(Q\) 的 KL 散度的定义:
\[\nonumber D_{KL}(P\Vert Q) = \mathbb{E}_P\left[\log\frac{P}{Q}\right]\]给定两个多元正态分布 \(P_1\) 和 \(P_2\), 我们有:
\[\nonumber \begin{align} \nonumber D(P_1\Vert P_2) &= \mathbb{E}_{P_1}[\log P_1 - \log P_2] \\ \nonumber &= \frac12\mathbb{E}_{P_1}[-\log\vert\pmb{\Sigma}_1\vert-(\pmb{x}-\pmb{\mu}_1)^T\pmb{\Sigma}_1^{-1}(\pmb{x}-\pmb{\mu}_1) + \log\vert\pmb{\Sigma}_2\vert+(\pmb{x}-\pmb{\mu}_2)^T\pmb{\Sigma}_2^{-1}(\pmb{x}-\pmb{\mu}_2)] \\ \nonumber &= \frac12\log\frac{\vert\pmb{\Sigma}_2\vert}{\vert\pmb{\Sigma}_1\vert} + \frac12\mathbb{E}_{P_1}[-(\pmb{x}-\pmb{\mu}_1)^T\pmb{\Sigma}_1^{-1}(\pmb{x}-\pmb{\mu}_1)+(\pmb{x}-\pmb{\mu}_2)^T\pmb{\Sigma}_2^{-1}(\pmb{x}-\pmb{\mu}_2)] \\ \nonumber &= \frac12\log\frac{\vert\pmb{\Sigma}_2\vert}{\vert\pmb{\Sigma}_1\vert} + \frac12\mathbb{E}_{P_1}[-\text{tr}(\pmb{\Sigma}_1^{-1}(\pmb{x}-\pmb{\mu}_1)(\pmb{x}-\pmb{\mu}_1)^T)+\text{tr}(\pmb{\Sigma}_2^{-1}(\pmb{x}-\pmb{\mu}_2)(\pmb{x}-\pmb{\mu}_2)^T)] \\ \nonumber &= \frac12\log\frac{\vert\pmb{\Sigma}_2\vert}{\vert\pmb{\Sigma}_1\vert} - \frac12 \text{tr}(\pmb{\Sigma}_1^{-1}\mathbb{E}_{P_1}[(\pmb{x}-\pmb{\mu}_1)(\pmb{x}-\pmb{\mu}_1)^T]) + \frac12 \text{tr}(\pmb{\Sigma}_2^{-1}\mathbb{E}_{P_1}[(\pmb{x}-\pmb{\mu}_2)(\pmb{x}-\pmb{\mu}_2)^T]) \\ \nonumber &= \frac12\log\frac{\vert\pmb{\Sigma}_2\vert}{\vert\pmb{\Sigma}_1\vert} - \frac12 \text{tr}(\pmb{\Sigma}_1^{-1}\pmb{\Sigma}_1) + \frac12 \text{tr}(\pmb{\Sigma}_2^{-1}(\pmb{\Sigma}_1+\pmb{\mu}_1\pmb{\mu}_1^T-2\pmb{\mu}_1\pmb{\mu}_2^T+\pmb{\mu}_2\pmb{\mu}_2^T)) \\ \nonumber &= \frac12\left(\log\frac{\vert\pmb{\Sigma}_2\vert}{\vert\pmb{\Sigma}_1\vert} - n + \text{tr}(\pmb{\Sigma}_2^{-1}\pmb{\Sigma}_1) + \text{tr}(\pmb{\mu}_1^T\pmb{\Sigma}_2^{-1}\pmb{\mu}_1-2\pmb{\mu}_2^T\pmb{\Sigma}_2^{-1}\pmb{\mu}_1+\pmb{\mu}_2^T\pmb{\Sigma}_2^{-1}\pmb{\mu}_2)\right) \\ \nonumber &= \frac12\left(\log\frac{\vert\pmb{\Sigma}_2\vert}{\vert\pmb{\Sigma}_1\vert} - n + \text{tr}(\pmb{\Sigma}_2^{-1}\pmb{\Sigma}_1) + (\pmb{\mu}_2-\pmb{\mu}_1)^T\pmb{\Sigma}_2^{-1}(\pmb{\mu}_2-\pmb{\mu}_1)\right) \end{align}\]正态分布随机变量的和
令 \(X\sim\mathcal{N}(\mu_X,\sigma_X^2)\) 和 \(Y\sim\mathcal{N}(\mu_Y,\sigma_Y^2)\) 是两个服从正态分布的随机变量, 且相互独立, 那么它们的和 \(Z=X+Y\) 也是一个正态分布, 且
\[Z\sim\mathcal{N}(\mu_X+\mu_Y,\sigma_X^2+\sigma_Y^2).\]该事实可以通过特征函数或者函数卷积来证明. 详见 《Sum of normally distributed random variables》 此处略去.
重参数化技巧
Kingma 等人在 《Auto-Encoding Variational Bayes》 提出了一种重参数化技巧, 可以简化建模过程的计算.
令 \(\bm{z}\) 是一个连续随机变量, 且 \(\bm{z}\sim q_{\phi}(\bm{z}\vert\bm{x})\) 是一个条件分布, 那么可以把随机变量 \(\bm{z}\) 表示为一个确切的变量 \(\bm{z}=g_{\phi}(\bm{\epsilon},\bm{x})\), 亦即从随机变量 \(\bm{z}\) 中剥离出其随机性, 赋予一个辅助随机变量 \(\bm{\epsilon}\sim p(\bm{\epsilon})\), 其中 \(g_{\phi}(\cdot)\) 是个向量值函数.
这种重参数化在某些情境下是十分有用的. 比如我们可以用这种方法重写 \(q_{\phi}(\bm{z}\vert\bm{x})\) 的期望, 这样关于该期望的蒙特卡洛估计关于 \(\phi\) 就是可微的.
再比如: 令 \(z\sim p(z\vert x) = \mathcal{N}(\mu, \sigma^2)\), 这样 \(z\) 可以重参数化为 \(z=\mu+\sigma\epsilon\), 其中 \(\epsilon\sim\mathcal{N}(0, 1)\).