在阅读 OpenAI 的 Scaling Laws 一文时, 看到了关于 batch size 的讨论. 这引导我们回来考古一下 2018 年 OpenAI 的一篇文章《An Empirical Model of Large-Batch Training》, 当时已经发现模型可以有效地用大 batch 训练, 而该文章发现不同 domain 下选择的 batch 可能会差几个数量级. 那么一个自然的问题是: 当我们有比较充足的计算资源, 并且希望充分且高效的利用这批计算资源时, 如何选择合适的 batch size 呢? 这篇文章为解决这个问题提出了 gradient noise scale 的概念.
直观理解
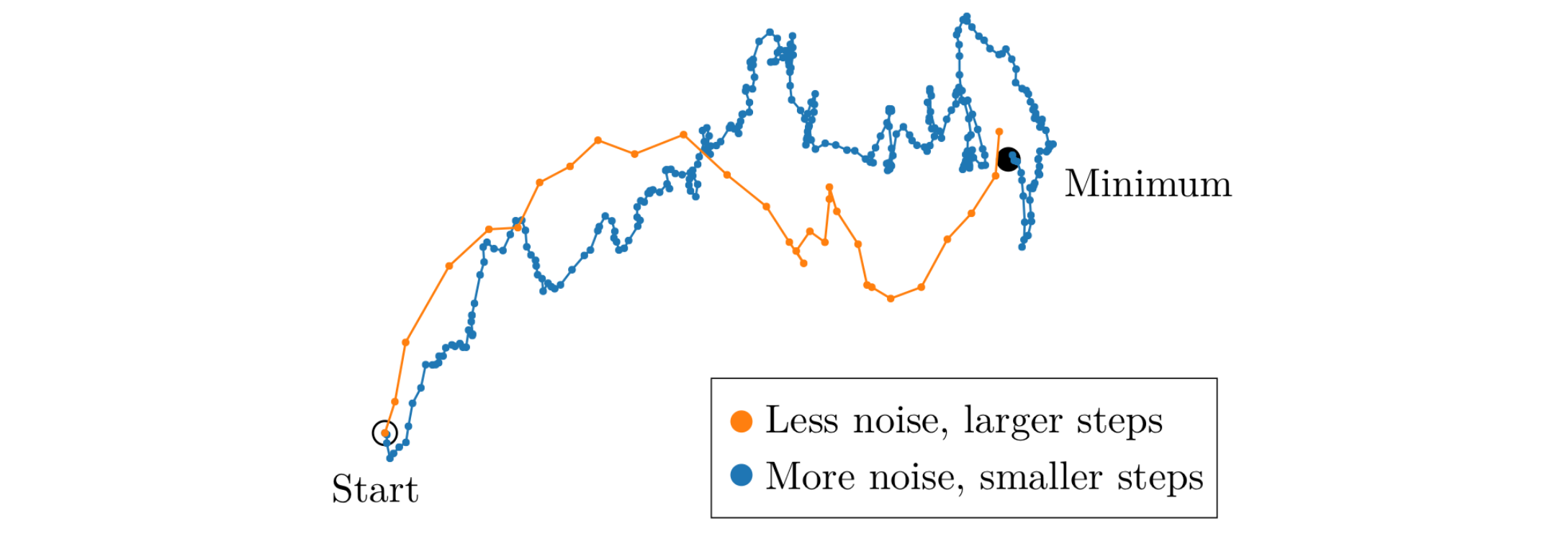
图 1. 大 batch 和小 batch 下参数的优化轨迹
我们首先要理解两种现象. 当 batch size 很小时, 由于数据中是存在噪声的, 因此每个 batch 的梯度会有一定的差异, 这样就会导致参数的更新方向不一致, 从而使得参数的更新轨迹不是很平滑. 当梯度更新的次数足够多的时候, 总体上参数才会向正确的方向前进. 如果我们直接把这些更新聚合成一次更新, 那么这个更新的方向就会是一个比较好的方向, 这也就引导我们使用大 batch size.
反过来, 当我们使用非常大的 batch size 时, 这一批数据的梯度会非常接近于真实的梯度, 那么在这个点上你随机采样两次会得到几乎一样的梯度, 这意味着此时你把 batch size 扩大一倍得到的仍然是几乎一样的梯度. 这就意味着此时你用了更多的计算资源(batch size 翻倍的话计算资源也需要翻倍), 但是得到的信息量却没有增加, 血亏!
此时再看图 2, 我们就能理解计算资源和训练时长是一个 tradeoff, 而这里的控制条件就是 batch size. 同时我们也知道了对于一个模型, 我们希望找一个尽可能靠近左下角的点(拐点), 用尽量少的资源和尽量少的时间训出模型.
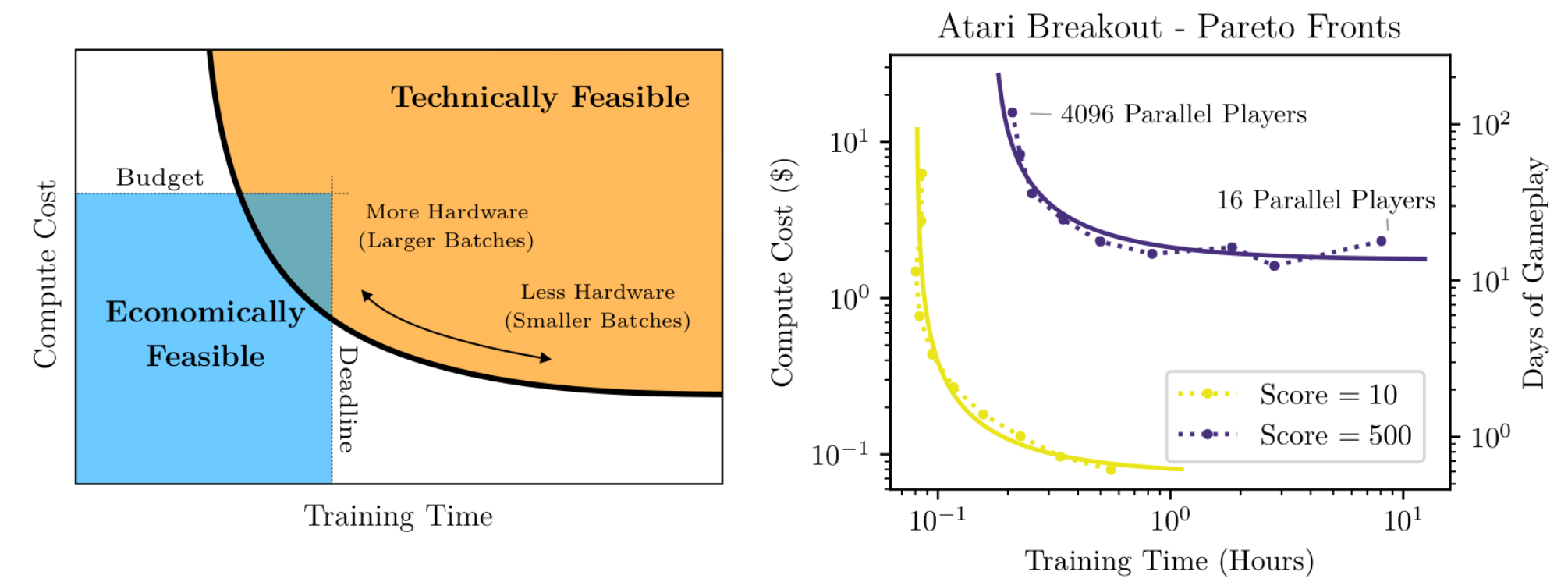
图 2. 计算资源和训练时间的 tradeoff
理论推导
我们用 \(L(\theta) = \mathbb{E}_{x\sim\rho}[L_x(\theta)]\) 来衡量模型表现, 其中 \(\theta\in\mathbb{R}^D\) 是模型的参数, \(\rho\) 是数据点 \(x\) 的分布. 然后我们用基于 SGD 的优化器来优化 \(L\) 时, 通过如下的公式来估计梯度:
\[ G_{\text{est}} = \frac1B\sum_{i=1}^B\nabla_{\theta} L_{x_i}(\theta), \quad x_i\sim\rho. \]
根据文章中 2.2 节的推导, 我们最终可以得到在 batch size 为 B 的时候一步更新所能带来的最优的损失下降:
\[\label{delta_L} \Delta L_{\text{opt}}(B) = \frac{\Delta L_{\max}}{1 + \mathcal{B}_{\text{noise}}/B}, \]
其中
\[\label{b_noise} \Delta L_{\max} = \frac12\frac{\vert G\vert^4} {G^THG}, \quad \mathcal{B}_{\text{noise}} = \frac{tr(H\Sigma)}{G^THG}. \]
这里的 \(\mathcal{B}_{\text{noise}}\) 称为 noise scale, 它衡量了梯度的噪声, 是一个和 batch size 无关的值.
再看公式 \(\eqref{delta_L}\), 当 \(B \ll \mathcal{B}_{\text{noise}}\) 时, 分母的第二项主导, 此时增大 batch size 会使得损失下降更快 (从而能够加速训练); 当 \(B \gg \mathcal{B}_{\text{noise}}\) 时, 分母的第一项主导, 此时增大 batch size 对损失下降的影响就不大了 (单纯浪费算力). 那么两种情况的分界点就是 \(B \approx \mathcal{B}_{\text{noise}}\), 这个点就是我们的最优的 batch size. 参见图 3 的第二幅图.
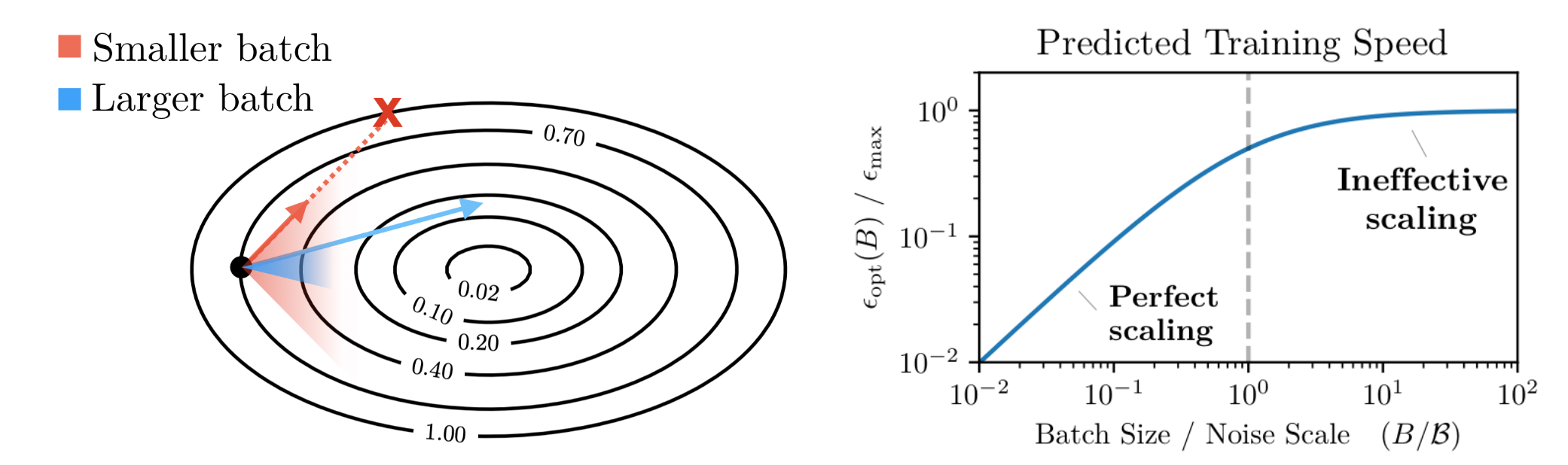
图 3. B 与 $$ \mathcal{B}_{\text{noise}} $$ 的相对大小对训练速度的影响
简化假设. 如果我们假设优化过程是完美的, 并且 Hessian 矩阵是单位矩阵的倍数,那么公式 \(\eqref{b_noise}\) 的第二部分可以简化为:
\[ \mathcal{B}_{\text{simple}} = \frac{tr(\Sigma)}{\vert G\vert^2}. \]
这个简化假设是不现实的, 但它让我们可以更容易地理解噪声尺度的定义.
噪声尺度的解释. 根据上面的公式, 噪声尺度可以理解为各个梯度分量方差的总和除以梯度的全局范数。这本质上是一个度量,衡量梯度的大小相对于其方差的比例。下面的公式给出了标准化 \(L^2\) 距离的期望值:
\[ \mathbb{E}\left[\frac{|G_{est} - G|^2} {|G|^2}\right] = \frac1B\frac{tr(\Sigma)}{\vert G\vert^2} = \frac{\mathcal{B}_{\text{simple}}}{B}. \]
这表示了估计梯度和真实梯度在 \(L^2\) 空间中接近的程度.