半监督学习(Semi-Supervised Learning, SSL)

1. Introduction
2. Consistency Regularization
3. Entropy Minimization
4. Proxy-Label Methods
- 4.1 Self-Training
- 4.2 Multi-View Training
5. Holistic Methods
6. Generative Models
7. Graph-Based SSL
8. Self-Supervision for SSL
参考文献

深度学习 (deep learning) 通过监督学习 (supervised learning) 在大量的机器学习任务上取得了瞩目的成就, 如 ImageNet 上超过 90% 的分类准确率, Cityscapes 上超过 85% 的分割准确率. 然而, 实现高精度的分类, 分割等任务需要大规模有标签的训练数据, 如 ImageNet 的百万张图像或是 Cityscapes 上数千张 1080p 分辨率图像的像素级标注, 都需要耗费大量的人力物力, 同时在这些数据上训练的模型往往在跨域的数据泛化上仍然具有挑战性 (如医学图像). 虽然数据标注难以获取, 但从多种渠道收集无标注数据是相对容易的, 因此研究者逐渐把目光转向如何利用少部分有标注数据和大规模的无标注数据来训练模型 (比如, 有标签数据占整体的 1-10%). 这种同时利用少量有标注数据和大量无标注数据训练模型的方法称为半监督学习 (semi-supervised learning, SSL).

1. Introduction

1.1 半监督学习

SSL 介于监督学习和无监督学习之间, 数据集 $X = \{x_i\}$ 可以分为两部分, 有标签的数据集 $X_l = \{(x_1, y_1), \dots, (x_l, y_l)\}$ 和无标签数据集 $X_u = \{x_{l+1}, \dots, x_{l+u}\}$. 我们可以从两个角度来看待半监督学习:

我们使用 $X_l$ 来确定分类边界, 并期望使用 $X_u$ 来更好地估计数据分布 $p(x)$, 从而更准确的确定分类边界. 如图 1 所示, 我们可以通过大量的无标签数据寻找低密度区域, 以更好地确定分类边界. 这类方法是比较经典的做法.

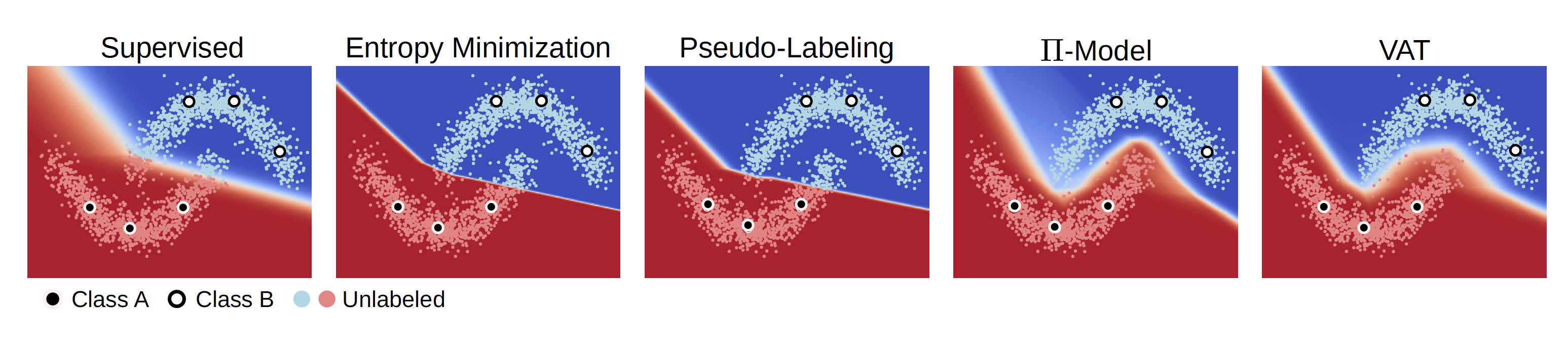
图 1. SSL toy example

我们首先使用 $X_u$ 基于自监督方法训练一个大模型, 然后使用 $X_l$ 对模型进行 finetune, 最后可以进一步蒸馏得到小模型以减少参数量¹. 这类方法是在自监督方法有了突破式的发展之后出现的.

1.2 分类

SSL 可以大致分类以下几类:

序号	分类	描述
1	Consistency Regularization	一致性约束方法. 数据扰动后, 特征/预测结果不应有显著变化. 从而通过约束扰动前后的数据对应的特征来训练模型.
2	Entropy Minimization	熵极小化. 鼓励模型预测高置信度的结果.
2	Proxy-Label Method	伪标签方法. 通过一个预训练模型对无标签数据打标签, 然后进一步利用打了伪标签的数据训练模型.
3	Generative Models	生成式模型. 结合 GAN 或 VAE, 从无标签数据中学习好的用于分类的判别器.
4	Graph-Based Methods	基于图的方法. 有标签数据和无标签数据可以看做图的节点, 目标是通过节点之间的相似性把有标签节点的标签传播到无标签节点.

此外, 还可以通过学习模式分为:

归纳学习 (Inductive Learning): 学习一个分类器, 从而可以泛化到 unseen 的测试数据集上.
直推式学习 (Transductive Learning): 在训练时同时利用测试数据以提高测试数据上的性能, 这种方法不要求泛化到新的测试数据上.

1.3 SSL 的假设

SSL 需要一些假设来保证从大规模无标签数据中学习知识是有效的.

光滑性假设 (Smoothness): 如果高密度区域的两个点 $x_1$ 和 $x_2$ 距离很近, 那么他们的预测结果 $y_1$ 和 $y_2$ 也应该很近. 反过来, 如果两个点被低密度区域分离, 那么他们的标签应当不同. 该假设对于分类问题是有用的, 但对于回归问题不然.
聚类假设 (Cluster): 如果两个点在同一个聚类, 那么它们很可能属于同一个类别. (聚类假设也可以看做是低密度分离假设, 即分类边界应当落在低密度区域.) 基于该假设, 我们就可以要求数据在局部扰动时, 其预测分类保持不变.
流形假设 (Manifold): 高维数据分布在一个低维流形上. 由于空间大小随着维度指数增长, 这对于建模来说是灾难性的. 然而有了流形假设, 我们可以寻找低维映射来建模数据.

这三个假设来源于 Chapelle 等人的 Semi-Supervised Learning 一书².

1.4 SSL 与其他任务的联系

SSL 和无监督域适应 (unsupervised domain adaptation, UDA) 是十分接近的任务, 他们都使用有标签和无标签的数据, 区别在于 SSL 的两类数据属于同一个域, 而 UDA 是源域是有标签数据, 目标域是无标签数据. 同时, 如果我们可以在 UDA 中通过一些方法 (如生成式方法) 把目标域数据变成源域数据, 此时我们就可以把众多 SSL 方法应用到 UDA 方法中.
SSL 与 learning from noisy labels 的任务有密切联系. 基于伪标签的 SSL 方法势必会遇到伪标签存在大量噪声的问题, 此时 SSL (包括基于伪标签的 UDA 方法) 可以应用 noisy labels 任务的方法.
SSL 还可以利用自监督学习, 通过自监督学习获得好的 warm-up model; 或在半监督学习的过程中, 引入自监督损失来对模型进行正则化 (一致性约束).
SSL 不同于弱监督学习 (weakly-supervised learning), 后者所有数据都有标签, 强调的是标签为弱标签. 比如分割任务只提供分类标签, 这与 SSL 的目标是不同的.

2. Consistency Regularization

一致性约束是对模型的一种正则化. 根据流形假设, 高维数据分布在一个低维流形上, 我们希望模型对于流形上相近数据点能给出相似的预测结果. 这一点是很自然的, 但是简单扰动后的数据并不一定能落在流形上, 而且我们实际上无法有效的去建模数据流形. 过去的诸多实验证明, 一致性约束是 SSL 一种有效的方法. Ghosh 等人³提出我们可以用 Manifold Tangent Classifier (MTC) 来近似数据流形, 也就是说, 给定流形上的一个数据点 $x$, 我们可以做过该点关于流形的切平面, 切平面是可以用一组正交基 $\mathbf{e}_1^x,\dots,\mathbf{e}_d^x$ 表示的, 这意味着

\[\hat{x} = x + \underbrace{\sum_{j=1}^d \omega_j\textbf{e}_j^x}_{V_{\omega}}\]

中系数 $w_j$ 足够小时, 切平面可以充分地近似流形. 因此当我们迫使 $f_{\theta}(x)$ 在 $x$ 的附近沿着流形近似为常数的时候, 我们实际上是在惩罚 $f_{\theta}(x)$ 在 $x$ 处的梯度. 具体地,

\[\mathbb{E}_{\omega}[\Vert f_{\theta}(x+V_{\omega}) - f_{\theta}(x)\Vert^2] \approx \mathbb{E}_{\omega}[\Vert \mathbf{J}_x V_{\omega}\Vert^2]\]

其中 $\mathbf{J}_x$ 是 $f_{\theta}$ 关于 $x$ 的 Jacobian 矩阵³. (泰勒展开)

此外, 一致性约束可以有多种度量距离的方法, 比较常用的包括 mean squared error (MSE), Kullback-Leiber Divergence (KL 散度) 和 Jensen-Shannon Divergence (JS 散度). 假设 $f_{\theta}(x)$ 和 $f_{\theta}(\hat{x})$ 是 $C$ 个类别上的分布, 且 $m=\frac12(f_{\theta}(x) + f_{\theta}(\hat{x}))$, 那么这三个度量可以写为:

\[\begin{align} d_{\text{MSE}}(f_{\theta}(x), f_{\theta}(\hat{x})) &= \frac1{C}\sum_{k=1}^C(f_{\theta}(x)_k - f_{\theta}(\hat{x})_k)^2 \\ d_{\text{KL}}(f_{\theta}(x), f_{\theta}(\hat{x})) &= \frac1{C}\sum_{k=1}^C f_{\theta}(x)_k \log\frac{f_{\theta}(x)_k}{f_{\theta}(\hat{x})_k} \\ d_{\text{JS}}(f_{\theta}(x), f_{\theta}(\hat{x})) &= \frac12 d_{\text{KL}}(f_{\theta}(x)_k, m) + \frac12 d_{\text{KL}}(f_{\theta}(\hat{x})_k, m) \\ \end{align}\]

注意我们也可以在两个扰动后的样本 $\hat{x}_1$ 和 $\hat{x}_2$ 上施加一致性约束.

2.1 Ladder Network

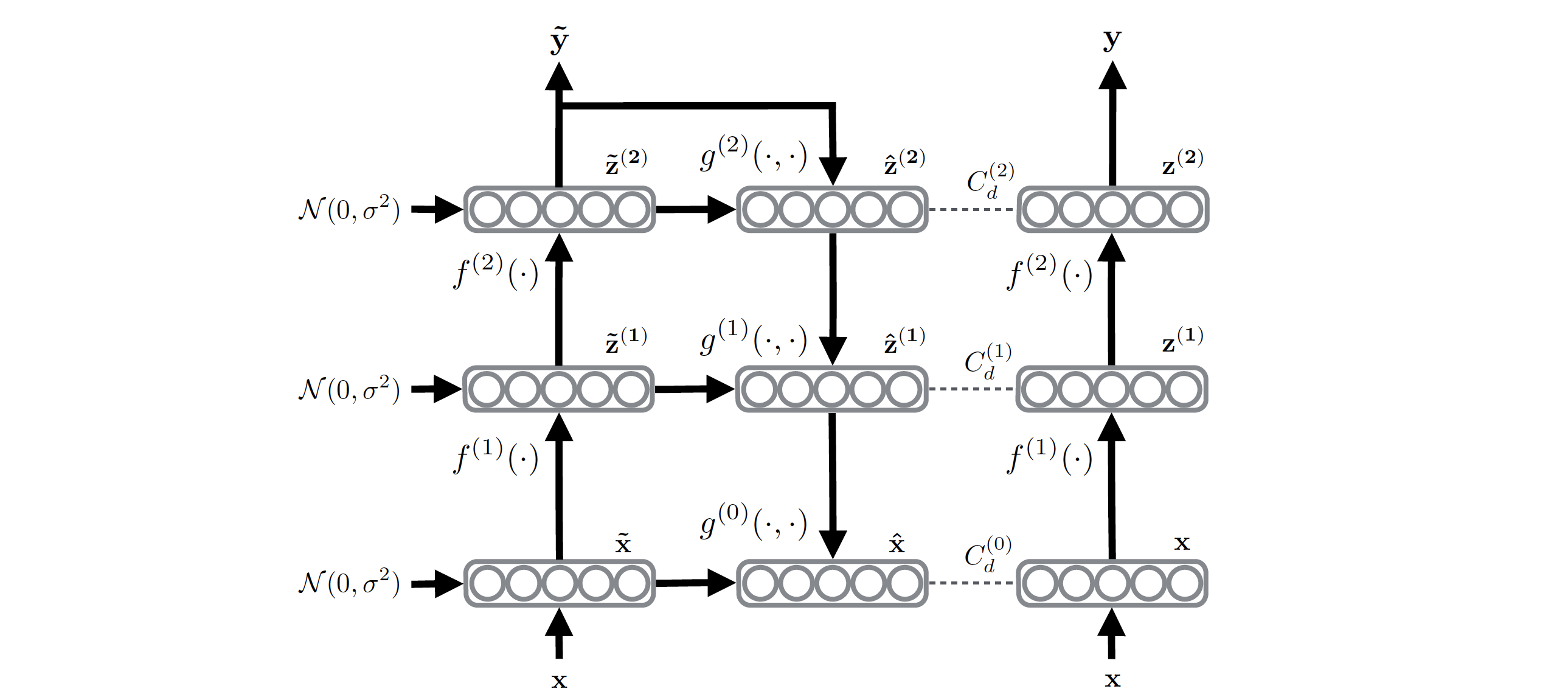
图 2. Ladder Network

Rasmus 等人提出使用 Ladder Network⁴, 最右侧的 encoder 对 $x$ 进行编码, 最左侧的 encoder 在编码过程中加入噪声, 然后通过 decoder 去噪, 同时在每一层的解码输出和右侧 encoder 的编码输出进行一致性约束.

\[\begin{align} \mathcal{L} &= \mathcal{L}_u + \mathcal{L}_s \\ &= \frac1{\vert D\vert}\sum_{x\in\mathcal{D}}\sum_{l=0}^L\lambda_l d_{\text{MSE}}(z^{(l)}, \hat{z}^{(l)}) + \frac1{\vert\mathcal{D}_l\vert}\sum_{x,t\in\mathcal{D}}H(\tilde{y},t) \end{align}\]

其中 $\mathcal{L}_u$ 是一致性约束, $\mathcal{L}_s$ 是交叉熵监督损失.

此外, 当 $l < L$ 时令 $\lambda_l=0$, 则这个 Ladder Network 的变体称为 $\Gamma\text{-Model}$.

2.2 $\Pi\text{-Model}$

图 3. $$ \Pi\text{-Model} $$

Laine 等人提出的 $\Pi\text{-Model}$ ⁵简化了 $\Gamma\text{-Model}$, 去除了加噪的 encoder, 只使用一个网络, 利用 augmentation 的输入和 dropout 来实现预测结果的扰动, 并进行约束:

\[\mathcal{L} = w\frac1{\vert \mathcal{D}_u\vert}\sum_{x\in\mathcal{D}_u}d_{\text{MSE}}(\tilde{y}_1,\tilde{y}_2) + \frac1{\vert\mathcal{D}_l\vert}\sum_{x,y\in\mathcal{D}_l}H(y, f(x))\]

其中 $w$ 是权重函数, 在训练的前一阶段 (如 20%) 从 0 增加到一个固定值 $\lambda$ (如 30), 以避免训练初期随机初始化的权重导致的不稳定的输出.

提示

对于 $\Gamma\text{-Model}$ 和 $\Pi\text{-Model}$, 我们发现前者是只对模型做扰动, 后者是同时对模型和输入数据做扰动.

2.3 Temporal Ensembling

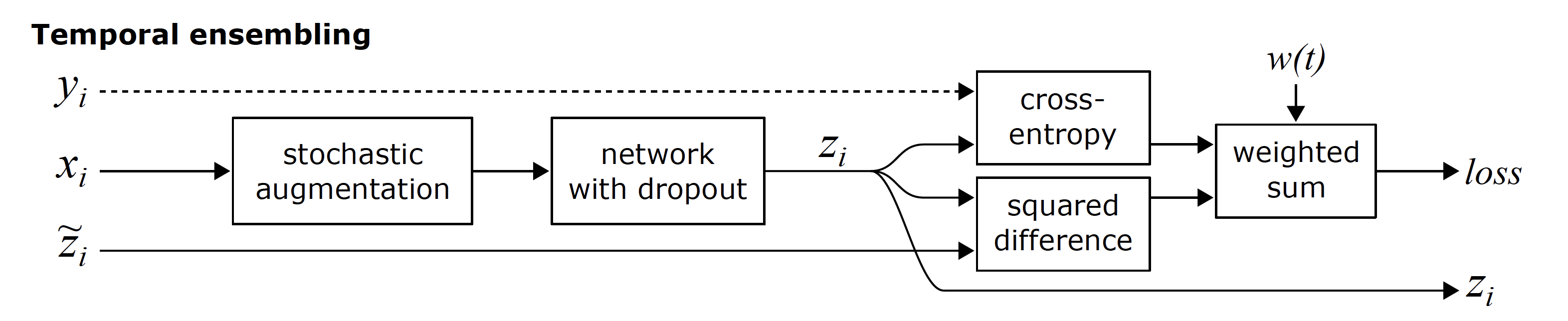
图 4. Temporal Ensembling

在 $\Pi\text{-Model}$ 中, 每个训练 step 可以分为两步: (1) 对数据进行 inference, 获得 prediction, (2) 把 prediction 作为无监督样本的 target, 利用不同的 augmentation 和 dropout 应该产生相同结果来目标来施加一致性约束. 但是, 考虑到单次 inference 的结果是不稳定的, 因此 Laine 等人⁵提出第二个版本的 $\Pi\text{-Model}$, 称为 Temporal Ensembling, 其中 target $y_{\text{ema}}$ 通过对所有前面预测结果的指数滑动平均 (exponential moving average, EMA) 来获得, 这样每个 step 只需要 inference 一次就能计算损失. 当前步的预测结果 $\tilde{y}$ 和 ensemble 的历史加权求和:

\[y_{\text{ema}} = \alpha y_{\text{ema}} + (1 - \alpha)\tilde{y}\]

其中 $\alpha$ 是加权系数, 通常取 0.99, 0.999 等较大的值以确保稳定性. 此外, 在训练初期, 由于预测结果不稳定, 因此通过一个偏置系数对结果进行修正 (类似于 Adam 优化器的做法):

\[y_{\text{ema}} = (\alpha y_{\text{ema}} + (1 - \alpha)\tilde{y}) / (1 - \alpha^t)\]

其中 $t$ 是训练的 step.

2.4 Mean Teachers

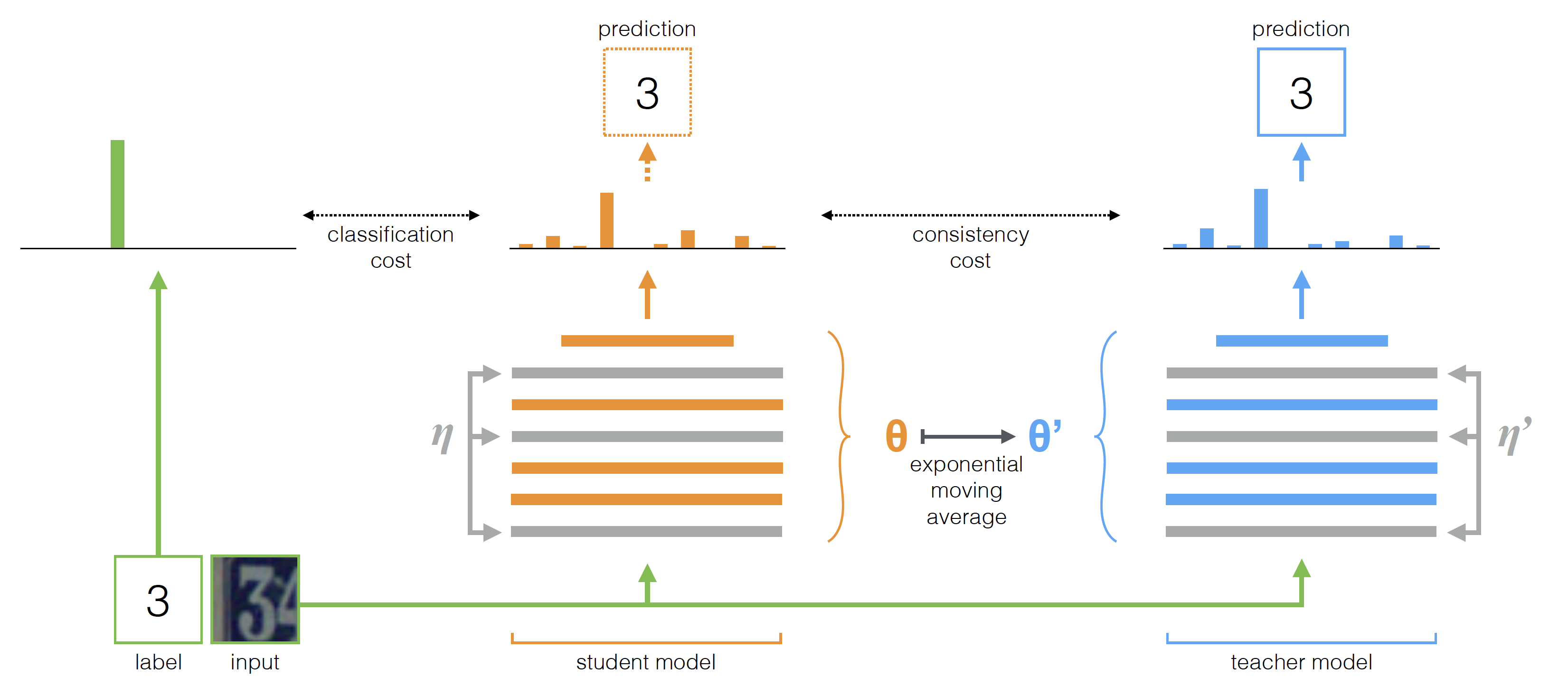
图 5. Mean Teachers

Temporal Ensembling 为每一个样本都记录了一个预测结果的 EMA, 但是最新学到的信息也会因为 EMA 模型而被以极其缓慢的速度加入到模型训练的过程中, 每个 epoch 只会更新一次. 同时, 在 $\Pi\text{-Model}$ 和 Temporal Ensembling 中, 同一个模型既当老师又当学生, 这样很容易让模型陷入 confirmation bias (即错误被自己放大). 因此, Mean Teacher 方法⁶被提出来解决这个问题. 与 Temporal Ensembling 不同的是, Mean Teacher 是对模型参数做 EMA, 而非样本的 predictions. 这样的好处是, 每一个 step 模型参数都会更新, 因此 EMA 模型作为 Teacher, 使用梯度更新的模型作为 Student, 可以提供更准确的 targets. 令 $\theta_t'$ 是 Teacher Model $f_{\theta'}$ 在 step $t$ 的参数, 则其更新方法为:

\[\theta_t' = \alpha \theta_{t-1}' + (1 - \alpha)\theta_t\]

因而损失函数计算为:

\[\mathcal{L} = w\frac1{\vert \mathcal{D}_u\vert}\sum_{x\in\mathcal{D}_u}d_{\text{MSE}}(f_{\theta}(x), f_{\theta'}(x)) + \frac1{\vert\mathcal{D}_l\vert}\sum_{x,y\in\mathcal{D}_l}H(y, f(x))\]

2.5 Dual Students

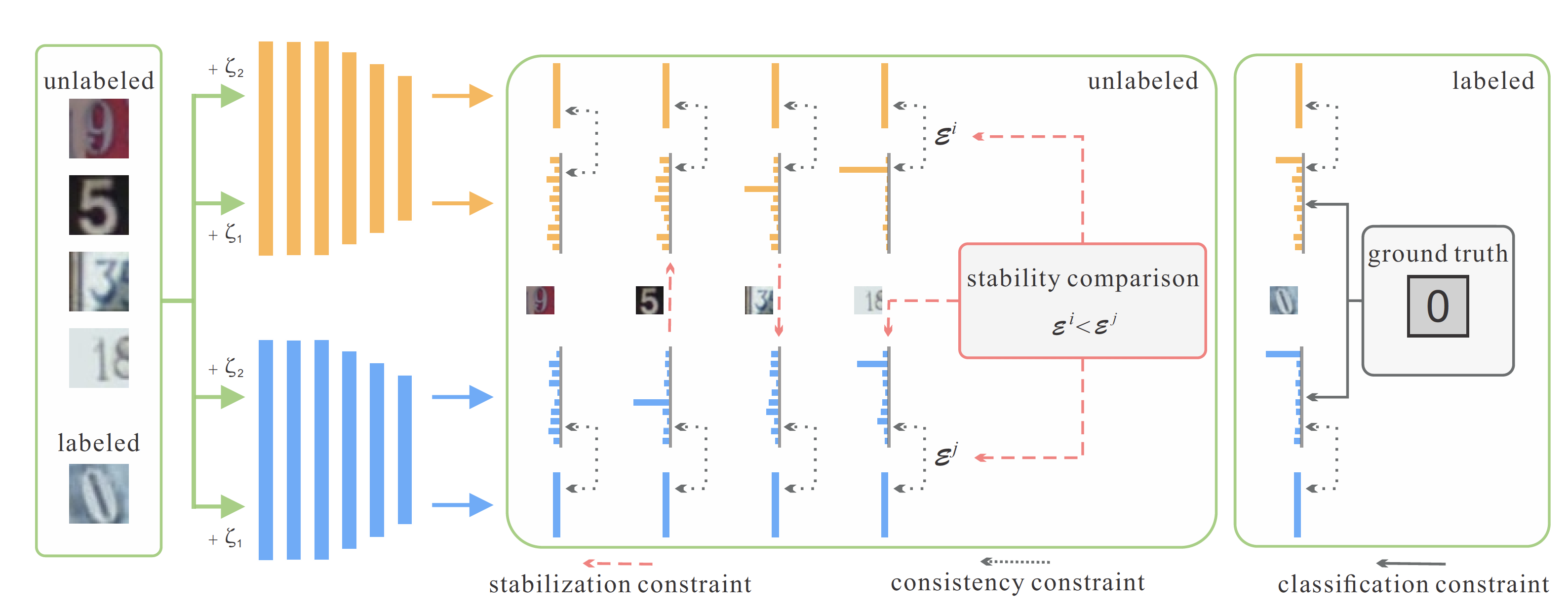
图 6. Dual Students

Mean Teacher 模型的一个主要的缺点是当训练时间足够长时, Teacher Model 的参数会收敛到 Student Model (假设 Student Model 最后是收敛的), 这样 Teacher 的作用就会随着训练的过程而弱化. Ke 等人提出了 Dual Students⁷ 来解决该问题, 即训练两个独立初始化的模型. 但是, 单纯训练两个独立的模型可能会导致结果相差较大, 而直接施加一致性约束的话又会导致两个模型交换错误的信息而形成模式坍缩变成一个模型, 因此 Dual Students 定义了 stable sample 的概念, 即 $x$ 和扰动点 $\tilde{x}$ 预测结果相同且离决策边界有一定距离的点. 定义

\[\mathcal{E}_i = \Vert f_{\theta^i}(x) - f_{\theta^i}(\tilde{x})\Vert^2\]

这样, 那些对两个模型都是 stable sample 的样本, 如果 $\mathcal{E}_i < \mathcal{E}_j$, 则模型 $i$ 作为模型 $j$ 的 Teacher; 只对其中一个模型是 stable sample 的样本, 令稳定模型是 Teacher, 对两个模型都不稳定的样本不参与梯度更新. 最终模型 $i$ 的损失为:

\[\begin{multline} \mathcal{L} = \frac1{\vert\mathcal{D}_l\vert}\sum_{x,y\in\mathcal{D}_l}H(y, f_{\theta^i}(x)) + \lambda_1 \frac1{\vert \mathcal{D}_u\vert}\sum_{x\in\mathcal{D}_u}d_{\text{MSE}}(f_{\theta^i}(x), f_{\theta^i}(\tilde{x})) \\ + \lambda_2 \frac1{\vert \mathcal{D}_u^{\text{ stable for } i}\vert}\sum_{x\in\mathcal{D}_u^{\text{ stable for } i}}d_{\text{MSE}}(f_{\theta^i}(x), f_{\theta^j}(x)) \end{multline}\]

2.6 Data Augmentation

把更多复杂的 Data Augmentation 方法应用于 SSL 的数据扰动, 如 MixUp⁸, AutoAugmentat⁹, RandAugment¹⁰ 等.

3. Entropy Minimization

聚类假设要求分类边界落在低密度区域, 除了上面的一致性约束方法外, 我们还可以对模型施加一个约束, 使其预测的结果更加 confident (而不管它预测的对与错), 这样的约束可以通过熵极小化的损失函数来实现:

\[-\sum_{k=1}^Cf_{\theta}(x)_k\log f_{\theta}(x)_k\]

单独使用熵极小化并不能带来精度上的提升, 因为该约束并不能让模型修正潜在的错误. 但是该方法与其他方法结合之后可以实现 SOTA 的效果.

Confidence Regularization

与 Entropy Minimization 相反的一个概念是 Confidence Regularization. 有时我们不能获得准确的标签 (比如伪标签方法, 带噪声的标签等等). 在这种情况下由于不确定标签的正确性, 因此我们希望模型预测的类别概率是留有余地的, 即任何类别都不应该预测出过高的概率, 这时候使用 Confidence Regularization 会更加有效. 比如对熵的正则化:

\[\sum_{k=1}^Cf_{\theta}(x)_k\log f_{\theta}(x)_k\]

或者使用 KL 散度让预测概率倾向于 uniform distribution:

\[-\sum_{k=1}^C\frac1K\log f_{\theta}(x)_k\]

4. Proxy-Label Methods

Proxy-Label 方法通常也称为伪标签 (pseudo-label) 方法, 是利用预训练模型对无标签数据打伪标签后, 和有标签数据结合起来训练模型的一类方法. 这类方法的典型实现有 self-training 和 multi-view training.

4.1 Self-Training

在 self-training 中, 首先使用有标签的 $\mathcal{D}_l$ 数据集训练一个分类器 $f_{\theta}$, 然后用该分类器对无标签数据 $x\in\mathcal{D}_u$ 打伪标签. 给定一个阈值 $\tau$, 如果 $\max f_{\theta}(x) > \tau$, 则把 $(x, \arg\max f_{\theta}(x))$ 加入训练集, 进一步训练模型. 迭代打伪标签和训练模型的步骤, 直到模型无法再产生 confident predictions. 当然, 为了进一步提高伪标签的质量, 可以对设置动态阈值, 或根据不同的类别设置不同的阈值等.

其他:

Pseudo-label and confirmation bias¹¹
Pseudo-label and label propagation¹²¹³

4.2 Multi-View Training

Multi-View Training 的一个代表性的工作是 Co-Training¹⁴. 在数据存在两个条件独立的 views 时, 使用两种 views 分别训练两个模型. 比如, 两个 views 可以是 RGB 和 Depth; 图像和文本等. 对于每个无标签数据, 如果在模型 $j$ 的预测结果高于阈值 $\tau$, 则把它加入模型 $i$ 的训练集, 从而实现两个模型相互监督训练.

其他:

Tri-Training¹⁵

5. Holistic Methods

Holistic 方法是把 SSL 已有的的不同路线的 SOTA 方法集成起来的一类方法, 代表性的工作主要是 Google 一系列的 *Match 方法.

5.1 MixMatch

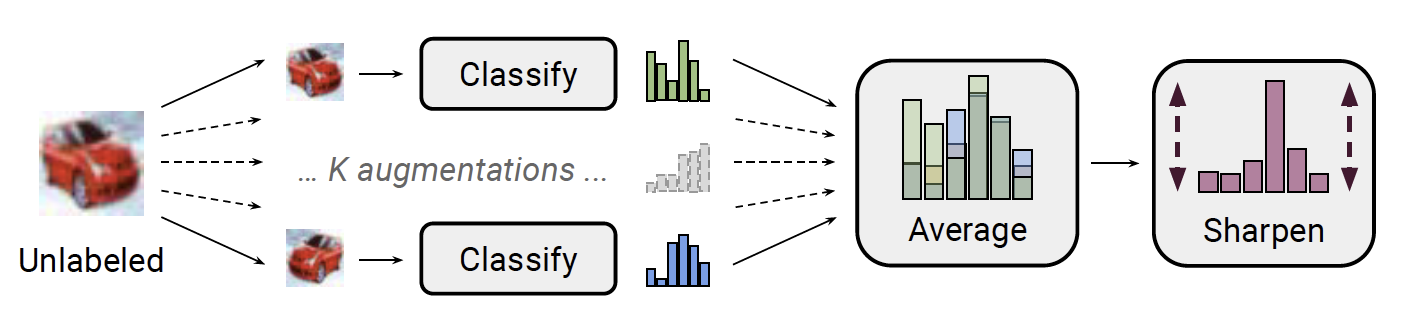
图 7. MixMatch

MixMatch¹⁶ 方法如下:

数据增广. 有标签数据 $(x_b, p_b)\in\mathcal{D}_l, b \in (1,\dots,B)$, 其中 $B$ 为 batch size, 计算其增广 $\hat{x}_b$. 无标签数据 $u_b\in\mathcal{D}_u, b \in (1,\dots,B)$, 计算其 $K$ 个增广 $\hat{u}_{b,1},\dots,\hat{u}_{b,K}$.
打伪标签. 这一步是给无标签数据打伪标签. 使用模型 $f_{\theta}$ 对 $K$ 个增广数据进行预测, 取平均预测结果作为 $K$ 个增广数据共同的伪标签
\[q_b = \frac1K\sum_{k=1}^K f_{\theta}(\hat{u}_{b,k})\]
锐化. 通过调整温度系数 $T$, 对上一步的伪标签结果进行锐化
\[\text{Sharpen}(q, T) = q_i^{\frac1T} \Big/ \sum_{j=1}^C q_j^{\frac1T}\]
其中 $C$ 是类别数.
MixUp. 在一个 batch 中, 对增广的有标签数据和增广的伪标签数据
\[\begin{align} \hat{\mathcal{X}} &= \{(\hat{x}_b, p_b); b \in (1,\dots, B)\} \\ \hat{\mathcal{U}} &= \{(\hat{u}_{b,k}, q_b); b \in (1,\dots,B), k \in (1,\dots,K) \} \end{align}\]
进行打乱得到混合数据 $\mathcal{W}=\text{Shuffle}(\text{Concat}(\hat{\mathcal{X}}, \hat{\mathcal{U}}))$. 然后再随机划分为和集合 $\hat{\mathcal{X}}, \hat{\mathcal{U}}$ 一样大小的 $\hat{\mathcal{W}}_1, \hat{\mathcal{W}}_2$. 接着使用 MixUp 生成新的增广数据:
\[\begin{align} \mathcal{X}' &= \text{MixUp}(\hat{\mathcal{X}}, \hat{\mathcal{W}}_1) \\ \mathcal{U}' &= \text{MixUp}(\hat{\mathcal{U}}, \hat{\mathcal{W}}_2) \end{align}\]
其中在使用 MixUp 时保证左侧集合占主导($\eqref{eq:mixup_lambda}$ 式), 即混合数据靠近左侧的数据. MixUp 方式如下:
\[\begin{align} \lambda &\sim \text{Beta}(\alpha, \alpha) \\ \label{eq:mixup_lambda} \lambda' &= \max(\lambda, 1-\lambda) \\ x' &= \lambda'x_1 + (1 - \lambda')x_2 \\ p' &= \lambda'p_1 + (1 - \lambda')p_2 \end{align}\]

最后使用 $\mathcal{X}'$ 和 $\mathcal{U}'$ 构造常规的 SSL 损失函数:

\[\begin{align} \mathcal{L} &= \mathcal{L}_s + w\mathcal{L}_u \\ &= \frac1{\vert\mathcal{X}'\vert}\sum_{x,p\in\mathcal{X}'}H(p, f_{\theta}(x)) + w\frac1{\vert\mathcal{U}'\vert}\sum_{u,q\in\mathcal{U}'}\Vert q-f_{\theta}(u)\Vert_2^2 \end{align}\]

5.2 ReMixMatch

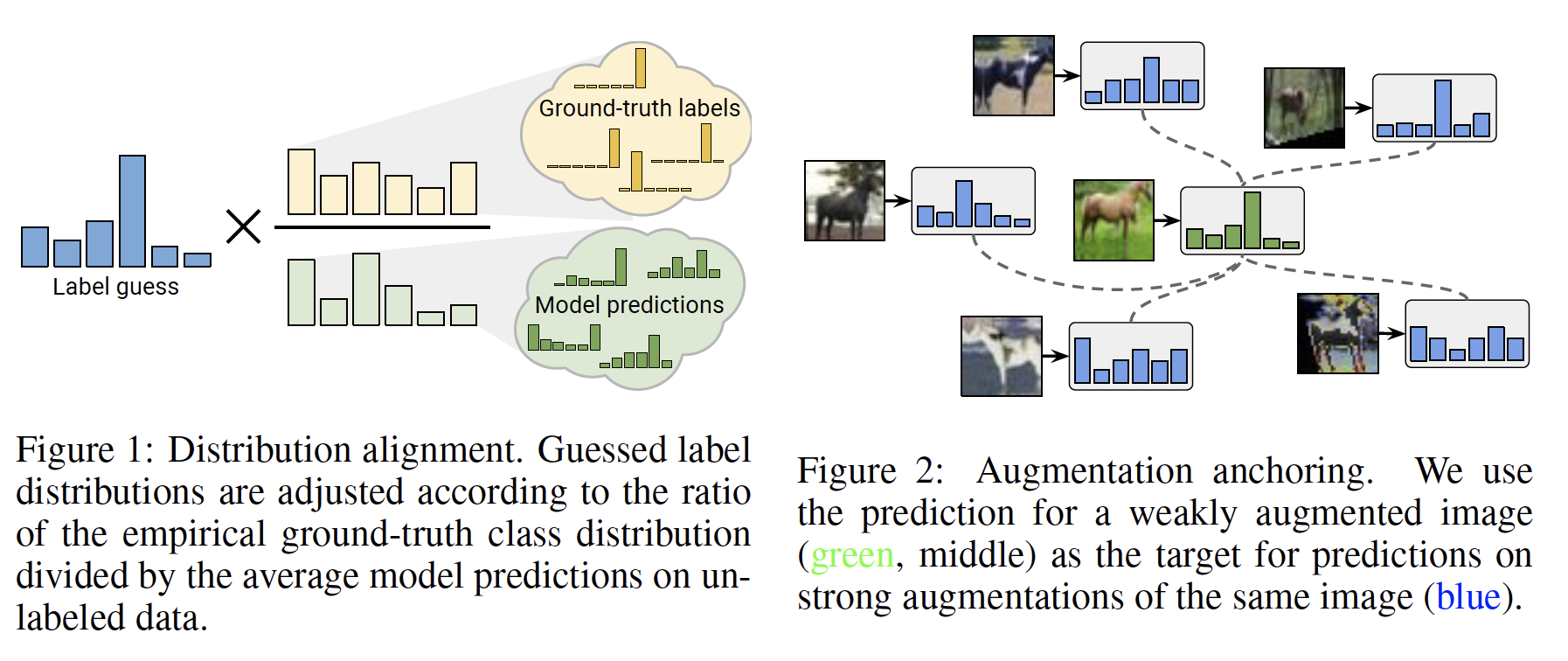
图 8. ReMixMatch: distribution alignment and augmentation anchoring

ReMixMatch¹⁷ 在 MixMatch 的基础上, 引入了两个新技术:

分布对齐 (distribution alignment): 要求无标签数据的预测(边缘)分布要对齐有标签数据的(边缘)分布
增广锚定 (augmentation anchoring): 要求多个强增广数据的预测接近弱增广数据的预测 (锚点).

5.3 FixMatch

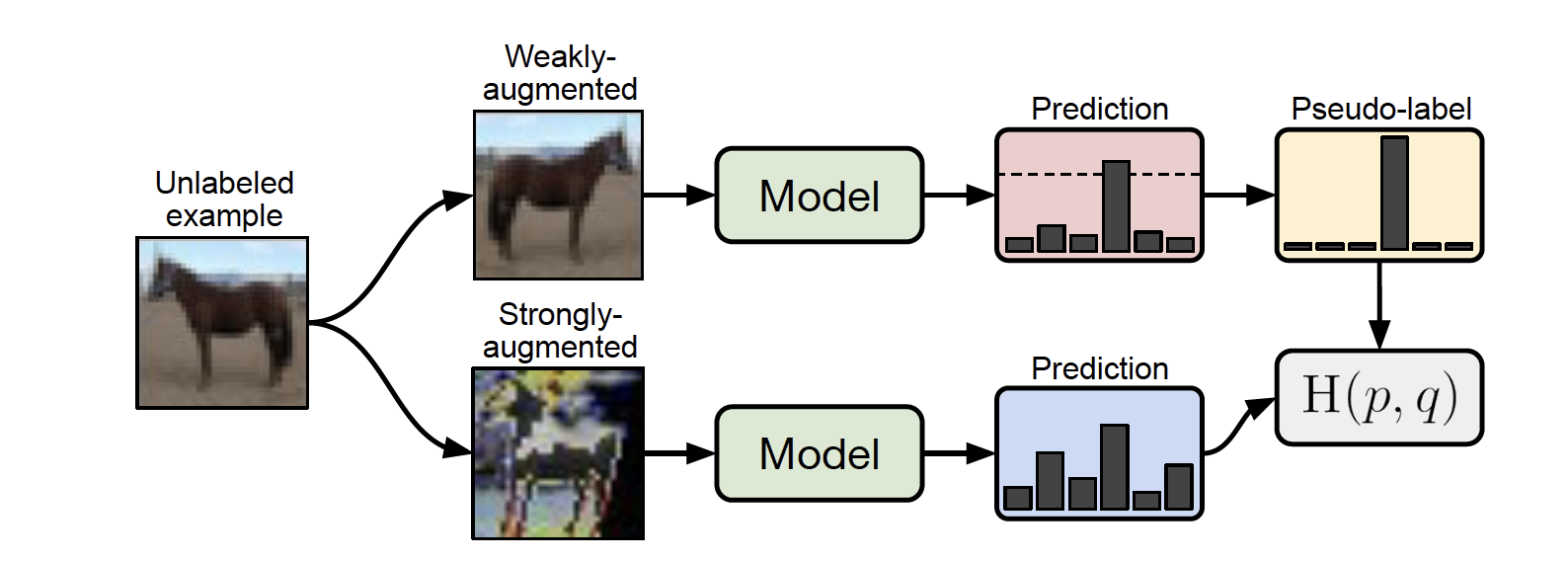
图 9. FixMatch

FixMatch¹⁸: 对于无标签数据, 如果模型 weakly-augmentated 样本的预测类别的置信度大于一个阈值, 则该类别当做伪标签用于训练 strongly-augmentated 的样本.

\[\mathcal{L}_u = \frac1{K\vert\mathcal{D}_u\vert}\sum_{x\in\mathcal{D}_u}\sum_{i=1}^K\mathbf{1}(\max(f_{\theta}(A_w(x))) \geq \tau)H(f_{\theta}(A_w(x)), f_{\theta}(A_s(x)))\]

其中 $A_w, A_s$ 分别表示 weakly-augmentation 和 strongly-augmentation.

6. Generative Models

7. Graph-Based SSL

8. Self-Supervision for SSL

参考文献

Big Self-Supervised Models are Strong Semi-Supervised Learners
T. Chen, S. Kornblith, K. Swersky, M. Norouzi, and G. Hinton
[pdf] In NeurIPS 2020 ↩
Semi-Supervised Learning (Book)
Chapelle O., Scholkopf B., Zien A. Eds
[html] In IEEE Transactions on Neural Networks 20, 542–542 (2009) ↩
On Data-Augmentation and Consistency-Based Semi-Supervised Learning
Ghosh A., Thiery A. H.
[html] In ICLR 2021 ↩ ↩²
Semi-Supervised Learning with Ladder Networks
Rasmus A., Valpola H., Honkala M., Berglund M., Raiko, T.
[html] In arXiv:1507.02672 ↩
Temporal Ensembling for Semi-Supervised Learning
S. Laine and T. Aila
[html] In arXiv:1610.02242 ↩ ↩²
Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results
A. Tarvainen and H. Valpola
[pdf] In NeurIPS 2017 ↩
Dual Student: Breaking the Limits of the Teacher in Semi-Supervised Learning
Z. Ke, D. Wang, Q. Yan, J. Ren, and R. W. H. Lau
[html] In CVPR 2019 ↩
MixUp: Beyond Empirical Risk Minimization
H. Zhang, M. Cisse, Y. N. Dauphin, and D. Lopez-Paz
[html] In ICLR 2018 ↩
AutoAugment: Learning Augmentation Policies from Data
E. D. Cubuk, B. Zoph, D. Mane, V. Vasudevan, and Q. V. Le
[html] In CVPR 2019 ↩
RandAugment: Practical automated data augmentation with a reduced search space
E. D. Cubuk, B. Zoph, J. Shlens, and Q. Le
[pdf] In NeurIPS 2020 ↩
Pseudo-Labeling and Confirmation Bias in Deep Semi-Supervised Learning
E. Arazo, D. Ortego, P. Albert, N. E. O’Connor, and K. McGuinness
[html] In IJCNN 2020 ↩
Label Propagation for Deep Semi-Supervised Learning
A. Iscen, G. Tolias, Y. Avrithis, and O. Chum
[html] In CVPR 2019 ↩
Learning from Labeled and Unlabeled Data with Label Propagation
X. Zhu and Z. Ghahramani
[pdf] In 2002 ↩
Combining labeled and unlabeled data with co-training
A. Blum and T. Mitchell
[html] In COLT 1998 ↩
Tri-training: exploiting unlabeled data using three classifiers
Zhi-Hua Zhou; Ming Li
[html] In TKDE 2005 ↩
MixMatch: A holistic approach to semi-supervised learning
D. Berthelot, N. Carlini, I. Goodfellow, N. Papernot, A. Oliver, and C. A. Raffel
[pdf] In NeurIPS 2019 ↩
ReMixMatch: Semi-Supervised Learning with Distribution Matching and Augmentation Anchoring
D. Berthelot
[html] In ICLR 2019 ↩
FixMatch: Simplifying semi-supervised learning with consistency and confidence
K. Sohn
[pdf] In NeurIPS 2020 ↩