奇异值分解(singular value decomposition)是线性代数中一种重要的矩阵分解,在信号处理、统计学等领域有重要应用。奇异值分解在某些方面与对称矩阵或厄米矩阵基于特征向量的对角化类似。然而这两种矩阵分解尽管有其相关性,但还是有明显的不同。对称阵特征向量分解的基础是谱分析,而奇异值分解则是谱分析理论在任意矩阵上的推广。
一个矩阵 \(A\) 的 SVD 分解 (Singular Value Decomposition) 指的是把 \(A\) 分解为三个矩阵的乘积
\[A=UDV^T,\]其中 \(U\) 和 \(V\) 各自的列向量是正交的, 而 \(D\) 是对角矩阵, 其元素都是正实数. SVD 分解有很多应用. 比如, 寻找一个矩阵的最优低秩近似矩阵, 实际上对于任意给定的秩, SVD 分解都可以给出最优近似; 不像特征分解只能用于方阵, SVD 分解对于所有的矩阵都是良好定义的(包括长方形的和正方形的矩阵). 特征分解要想获得正交的特征向量, 往往需要对待分解的矩阵做一定的约束, 如对称性. 而 SVD 分解的矩阵 \(V\) 的列向量(也称为右奇异向量)总是正交的. \(U\) 的列称为左奇异向量, 也是正交的. 正交性的一个很简单的结果就是: 如果矩阵 \(A\) 是方阵且可逆, 那么 \(A\) 的逆矩阵为
\[A^{-1} = VD^{-1}U^T.\]为了更直观的理解 SVD, 我们把一个尺寸为 \(n\times d\) 的矩阵 \(A\) 看成 \(d\)-维空间中的 \(n\) 个点.
\[A= \left( \begin{matrix} x_{11} & x_{12} & x_{13} & \cdots & x_{1d} \\ x_{21} & x_{22} & x_{23} & \cdots & x_{2d} \\ x_{31} & x_{32} & x_{33} & \cdots & x_{3d} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & x_{n3} & \cdots & x_{nd} \\ \end{matrix} \right) =\left( \begin{matrix} \mathbf{x}_1 \\ \mathbf{x}_2 \\ \mathbf{x}_3 \\ \vdots \\ \mathbf{x}_n \end{matrix} \right)\]考虑寻找最优 \(k\)-维子空间的问题. 这里的最优指的是极小化 \(n\) 个点到子空间垂直距离的平方和. 我们首先考虑最简单的 \(1\)-维子空间, 即通过原点的一条直线. 后面我们会说明对于更高维 \((k>1)\) 子空间的情况只需要把直线的结论应用于 \(k\) 个正交的方向上即可. 寻找最优拟合直线就是寻找一族点 \({\mathbf{x}_i\vert 1\leq i\leq n}\) 到过原点的直线的最短距离平方和, 这个问题称为最优最小二乘拟合(best least squares fit, BLSF).
下图给出了 \(d=2, n=2, k=1\) 的情况.
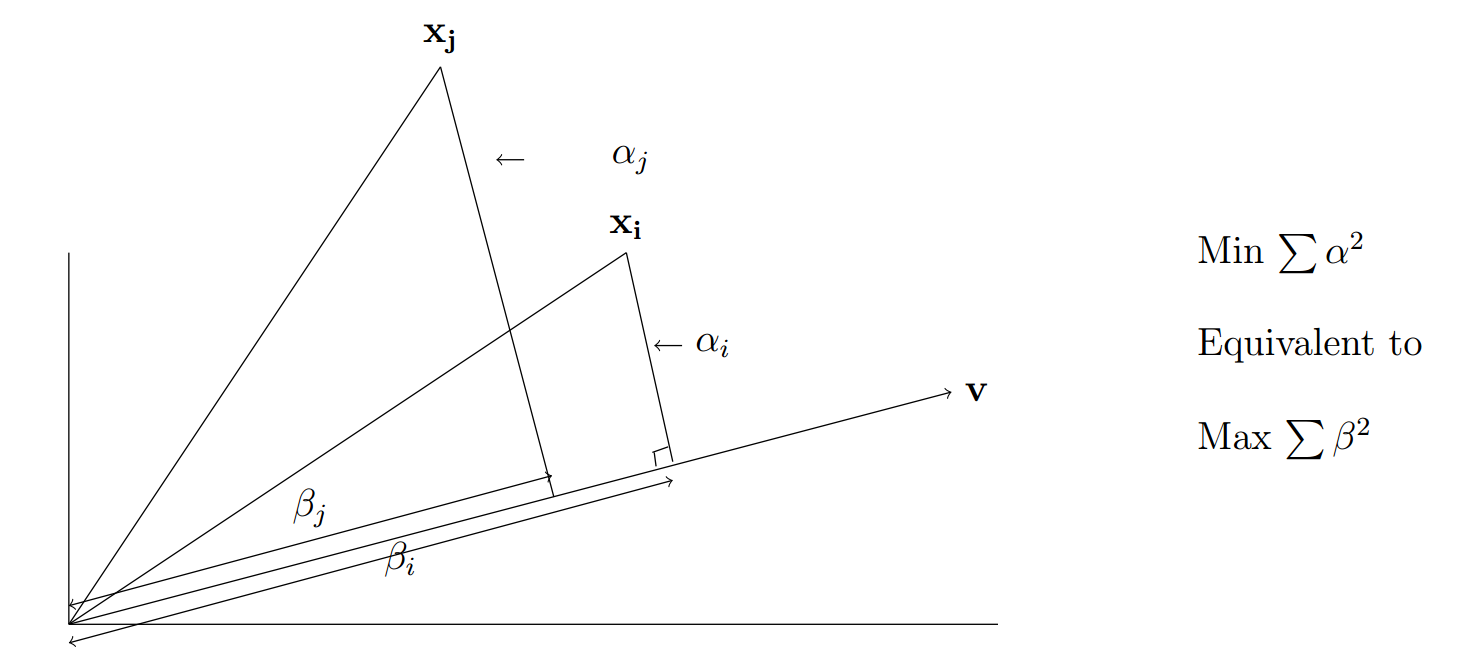
图 1. 点 x 在 v 方向上的投影
根据勾股定理, 我们有
\[\sum_{j=1}^d x_{ij}^2=\underbrace{\sum_{j=1}^d \alpha_j^2}_{距离平方和} + \underbrace{\sum_{j=1}^d\beta_j^2}_{投影平方和}.\]我们的目标是极小化 \(\sum_{j=1}^d \alpha_j^2\), 而 \(\sum_{j=1}^d x_{ij}^2\) 是固定值, 因此等价于极大化 \(\sum_{j=1}^d\beta_j^2\). 因此我们可以把极小化到子空间距离平方和的目标等价地变成极大化子空间上的投影平方和.
1. 奇异向量
我们在这一节定义矩阵 \(A\in\mathbb{R}^{n\times d}\) 的奇异向量(singular vector). 考虑过原点的最优拟合直线(见图1), 定义其单位方向向量为 \(\mathbf{v}\). 那么 \(\mathbf{x}_i\) 的投影长度为 \(\vert\mathbf{x}_i\cdot\mathbf{v}\vert\). 所以投影平方和为 \(\vert A\mathbf{v}\vert^2\). 所以最优拟合直线就是极大化 \(\vert A\mathbf{v}\vert^2\) 的那一条直线(同时极小化了距离平方和).
我们把第一奇异向量(列向量) \(\mathbf{v}_1\) 定义为
\[\mathbf{v}_1 = \underset{\vert\mathbf{v}\vert=1}{\arg\max}\vert A\mathbf{v}\vert.\]对应的值 \(\sigma_1(A)=\vert A\mathbf{v}\vert\) 称为 \(A\) 的第一奇异值. 注意 \(\sigma_1^2\) 就是所有点到第一奇异向量的投影平方和.
接下来我们可以通过贪婪法寻找矩阵 \(A\) 的最优 \(2\)-维子空间, 即使用 \(\mathbf{v}_1\) 作为该子空间的第一个基向量, 寻找包含 \(\mathbf{v}_1\) 的最优 \(2\)-维子空间. 注意到我们使用的是平方距离, 所以对于每个包含 \(\mathbf{v}_1\) 的 \(2\)-维子空间, 投影平方和等于在 \(\mathbf{v}_1\) 上的投影平方和加上在与其垂直方向的投影平方和(根据勾股定理). 我们记这个垂直方向的单位向量为 \(\mathbf{v}_2\). 那么只需要寻找垂直于 \(\mathbf{v}_1\) 且极大化 \(\vert A\mathbf{v}\vert^2\) 的单位向量. 如此, 第二奇异向量定义为:
\[\mathbf{v}_2 = \underset{\mathbf{v}\perp\mathbf{v}_1,\;\vert\mathbf{v}\vert=1}{\arg\max}\vert A\mathbf{v}\vert.\]类似的, 第三奇异向量定义为:
\[\mathbf{v}_3 = \underset{\mathbf{v}\perp\mathbf{v}_1,\mathbf{v}_2\;\vert\mathbf{v}\vert=1}{\arg\max}\vert A\mathbf{v}\vert.\]这样的过程一直做下去, 直到找到
\[\mathbf{v}_1,\;\mathbf{v}_2,\;\dots,\;\mathbf{v}_r\]使得
\[\underset{\mathbf{v}\perp\mathbf{v}_1,\mathbf{v}_2,\dots\mathbf{v}_r,\;\vert\mathbf{v}\vert=1}{\arg\max}\vert A\mathbf{v}\vert = 0.\]可以证明, 通过这样的贪婪算法找到的是每个维度的最优子空间. 证明略(见原文).
注意到 \(n\)-维向量 \(A\mathbf{v}_i\) 实际上是 \(A\) 的行向量在 \(\mathbf{v}_i\) 上投影的长度组成的向量(带符号). 把 \(\vert A\mathbf{v}_i\vert=\sigma_i(A)\) 看做矩阵 \(A\) 沿着 \(\mathbf{v}_i\) 的”成分”, 那么按照这个说法, 我们希望每个方向的”成分”的平方和恰好等于矩阵 \(A\) 的总量. 下面我们证明这个结论.
因为 \(\mathbf{v}_1,\;\mathbf{v}_2,\;\dots,\mathbf{v}_r\) 张成了矩阵 \(A\) 的行空间, 而对于任意垂直于 \(\mathbf{v}_1,\;\mathbf{v}_2,\;\dots,\mathbf{v}_r\) 的向量 \(\mathbf{v}\), 都有 \(\mathbf{x}_i\cdot\mathbf{v}=0\). 因此, 对于每个行向量 \(\mathbf{x}_j\), 都有 \(\sum_{i=1}^r(\mathbf{x}_j\cdot\mathbf{v}_i)^2=\vert\mathbf{x}_j\vert^2\). 把所有的行加起来, 得到
\[\begin{align} \nonumber \sum_{j=1}^n\vert\mathbf{x}_i\vert^2 &=\sum_{j=1}^n\sum_{i=1}^r(\mathbf{x}_i\cdot\mathbf{v}_i)^2 \\ &=\sum_{i=1}^r\sum_{j=1}^n(\mathbf{x}_i\cdot\mathbf{v}_i)^2=\sum_{i=1}^r\vert A\mathbf{v}_i\vert^2=\sum_{i=1}^r\sigma_i^2(A). \end{align}\]又有 \(\sum_{j=1}^n\vert\mathbf{x}_i\vert^2=\sum_{j=1}^n\sum_{k=1}^dx_{jk}^2\), 所以 \(A\) 的奇异值的平方和的确是 \(A\) 的”总量”, 所有元素的平方和, 后者通常称为 Frobenius 范数(模), 记为:
\[\Vert A\Vert_F=\sqrt{\sum_{i=1}^n\sum_{j=1}^dx_{ij}^2}\]于是我们得到如下的引理.
对于任意矩阵 \(A\), 其奇异值的平方和等于其 Frobenius 范数的平方. 即 \(\sum\sigma_i^2(A)=\Vert A\Vert_F^2.\)
矩阵 \(A\) 可以完全用它是如何变换向量 \(\mathbf{v}_i\) 的来描述. 任意向量 \(\mathbf{v}\) 可以写成 \(\mathbf{v}_1,\;\mathbf{v}_2,\;\dots,\mathbf{v}_r\) 和一个与他们垂直的向量的线性组合. 所以可以推出 \(A\mathbf{v}\) 是 \(A\mathbf{v}_1,\;A\mathbf{v}_2,\;\dots,A\mathbf{v}_r\) 的线性组合. 因此后者就形成了一族与 \(A\) 所关联的向量的基. 我们把他们做一个标准化:
\[\label{eq:left} \mathbf{u}_i=\frac1{\sigma_i(A)}A\mathbf{v}_i.\]向量 \(\mathbf{u}_1,\;\mathbf{u}_2,\;\dots,\mathbf{u}_r\) 称为 \(A\) 的左奇异向量. 而 \(\mathbf{v}_i\) 称为右奇异向量.
根据定义, 我们知道右奇异向量是正交的, 接下来我们证明左奇异向量也是正交的, 并且 \(A=\sum_{i=1}^r\sigma_i\mathbf{u}_i\mathbf{v}_i^T\).
令 \(A\) 是一个秩为 \(r\) 的矩阵, 那么 \(A\) 的左奇异向量 \(\mathbf{u}_1,\;\mathbf{u}_2,\;\dots,\mathbf{u}_r\) 是正交的.
2. 奇异值分解
令 \(A\) 是一个 \(n\times d\) 的矩阵, 奇异向量为 \(\mathbf{v}_1,\;\mathbf{v}_2,\;\dots,\mathbf{v}_r\), 对应的奇异值为 \(\sigma_1,\;\sigma_2,\;\dots,\sigma_r\). 根据定理1, 左奇异向量为 \(\mathbf{u}_1,\;\mathbf{u}_2,\;\dots,\mathbf{u}_r\). 那么, 矩阵 \(A\) 可以分解为如下秩为1的矩阵之和:
\[\label{eq:svd} A = \sum_{i=1}^r\sigma_i\mathbf{u}_i\mathbf{v}_i^T.\]我们有如下引理:
矩阵 \(A\) 和矩阵 \(B\) 是相等的, 当且仅当对于任意向量 \(\mathbf{v}\), 有 \(A\mathbf{v}=B\mathbf{v}\).
根据该引理, 我们可以得到奇异值分解定理:
令 \(A\in\mathbb{R}^{n\times d}\), 右奇异向量为 \(\mathbf{v}_1,\;\mathbf{v}_2,\;\dots,\mathbf{v}_r\), 左奇异向量为 \(\mathbf{u}_1,\;\mathbf{u}_2,\;\dots,\mathbf{u}_r\), 对应的奇异值为 \(\sigma_1,\;\sigma_2,\;\dots,\sigma_r\). 那么 \(A=\sum_{i=1}^r\sigma_i\mathbf{u}_i\mathbf{v}_i^T.\)
上面的分解称为 \(A\) 的奇异值分解, SVD. 用矩阵记号可以表示为 \(A=UDV^T\), 其中 \(U\) 和 \(V\) 的列向量是左右奇异向量, \(D\) 是对角矩阵, 对角元为奇异值.
对于任意矩阵 \(A\), 奇异值序列都是唯一的. 如果所有奇异值都不同, 那么所有的奇异向量也是唯一的; 反之, 奇异值相同的奇异向量就可以张成子空间, 子空间里任意的正交单位向量都可以作为奇异向量.
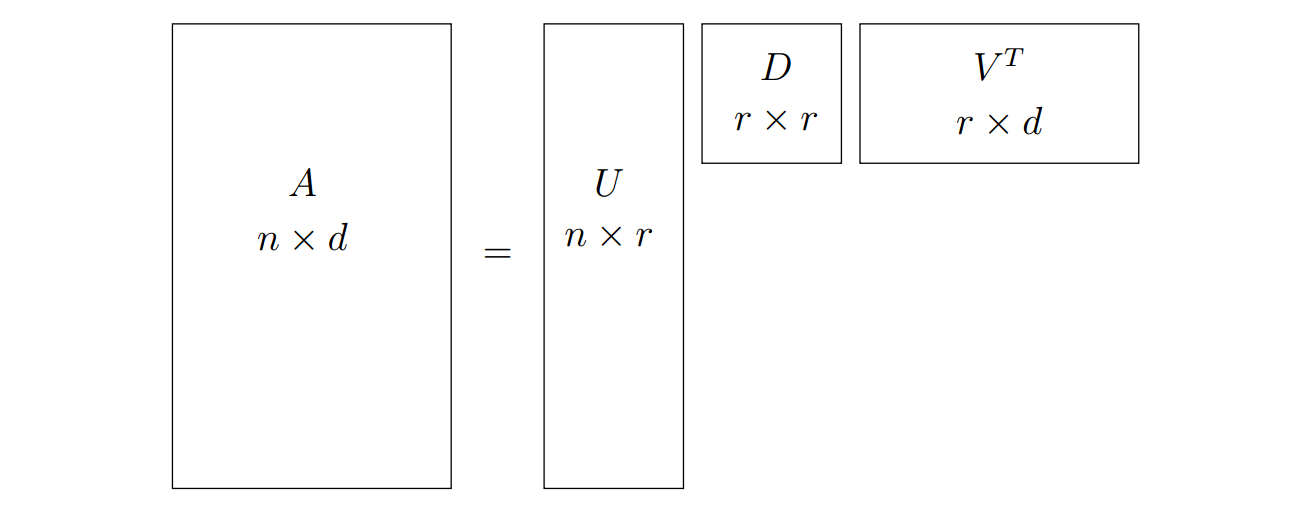
图 2. SVD 分解
3. 最优秩 \(k\) 近似
矩阵的 Forbenius 范数和 \(2\)-范数分别记为 \(\Vert A\Vert_F\) 和 \(\Vert A\Vert_2\). 其中 \(2\)-范数
\[\max_{\vert\mathbf{v}\vert=1}\vert A\mathbf{v}\vert\]等于矩阵最大的奇异值. 如果把 \(A\) 的行向量看做 \(d\)-维空间的点, 那么
- Frobenius 范数等于这些点到原点的欧氏距离之和的平方根.
- \(2\)-范数等于这些点在任意给定方向上的投影点到原点的欧氏距离之和的平方根的最大值.
考虑式 \(\eqref{eq:svd}\), 对于 \(k\in\{1,2,\dots,r\}\), 令
\[A_k = \sum_{i=1}^k\sigma_i\mathbf{u}_i\mathbf{v}_i^T\]是截断的前 \(k\) 项. 显然 \(A_k\) 的秩为 \(k\). 进一步, \(A_k\) Frobenius 范数和 \(2\)-范数的度量下 \(A\) 的最优秩 \(k\) 的近似. 我们通过两个引理和两个定理来陈述该事实. 首先讨论 Frobenius 范数:
\(A_k\) 的行向量是 \(A\) 的行向量在子空间 \(V_k\) 上的投影, 其中 \(V_k\) 由 \(A\) 的前 \(k\) 个奇异向量张成的.
然后我们有定理:
对于任意秩至多为 \(k\) 的矩阵 \(B\), 有 \(\Vert A-A_k\Vert_F\leq\Vert A-B\Vert_F.\)
接下来给出 \(2\)-范数的结论:
\(\Vert A-A_k\Vert_2^2=\sigma_{k+1}^2.\)
假设 \(A\in\mathcal{R}^{n\times k}\). 对任意秩至多为 \(k\) 的矩阵 \(B\), 有 \(\Vert A-A_k\Vert_2\leq\Vert A-B\Vert_2.\)