深度学习中主要的特征提取方式来源于离散卷积(convolution)操作, 至今为止卷积操作已经广泛应用于图像, 音频, 视频等的特征提取过程中, 同时为了适用于不同的任务或达到一定的目的, 卷积也产生了许多变种, 如: depthwise卷积, 分组卷积, 转置卷积, 膨胀卷积等等. 本文的目的有二, 一个是总结普通卷积核转置卷积的方式(填充, 步长)对输出图像大小的影响, 另一个是总结目前比较流行的卷积模块设计, 并尽量理清其思路.
注: 本文部分内容, 图片和gif来源于Dumoulin和Visin的开源项目Github:vdumoulin/conv_arithmetic.
第1章 引言
深度卷积神经网络(deep convolutional neural networks, CNNs)已经成为深度学习中的核心方法, 其在多种任务上的模型表现都令人惊叹. 尽管CNNs在上世纪九十年代就已经用于解决字符识别1的问题, 但目前广泛使用的深度CNNs模型来源于2012年Krizhevsky在ImageNet分类挑战中取得state-of-the-art的工作2.
卷积神经网络虽然成为深度学习中重要的组成部分, 但卷积操作本身并不像全连接(fully connected)那样简单, 它输出的特征大小同时受到输入特征的大小, 卷积核大小, 填充, 步长的影响. 此外, 膨胀卷积(atrous convolution)/或者叫空洞卷积(dilated convolution)的出现使得卷积变得更为复杂.
本文第一章为引言; 第2章对通常的卷积, 反卷积和空洞卷积做一个总结, 内容来源于Dumoulin和Visin的一篇技术报告3和DeepLab相关的科研工作[^4];第3章总结一些流行的卷积模块设计方法(持续更新).
1.1 离散卷积(discrete convolution)
在讨论卷积之前我们首先给出神经网络的基本要素, 即仿射变换(affine transformation): 一个向量 \(\mathbf{x}\in\mathbb{R}^m\) 左乘上一个矩阵 \(\mathbf{W}\in\mathbb{R}^{m\times n}\), 然后输出另一个向量 \(\mathbf{y}\in\mathbb{R}^n\), 通常还会加上一个偏置(bias)向量 \(\mathbf{b}\in\mathbb{R}^n\), 公式表示如下
\[\mathbf{y = Wx + b}. \label{eq:affine}\]然后输出的 \(\mathbf{y}\) 被非线性函数映射到下一层的输入. 这种仿射变换\(\eqref{eq:affine}\)通常称为全连接层, 我们也把得到的\(\mathbf{y}\)叫做提取出来的特征, 输入的向量\(\mathbf{x}\)称为特征向量. 通常来说我们处理的多属性的数据, 图像, 时序数据等有着不同的特征结构:
- 多属性的数据: 每个数据点包含 \(n\) 个属性值, 形成一个 \(n\) 维向量. 不同数据点的特征向量长度相同. 比如一个鸢尾花(iris)的数据点包含的五个属性(种属, 萼片长度, 萼片宽度, 花瓣长度, 花瓣宽度)构成了一个五维特征向量.
- 图像: 每幅图像看作一个数据点, 图像的高度和宽度为 \(h\) 和 \(w\), 包含 \(h\times w\) 个属性值, 形成一个二维矩阵. 不同数据点的长宽可能均不同. 图像的两个维度称为空间维度.
- 时序数据: 每段时序数据看作一个数据点, 每个时间点包含 \(n\) 个属性, 时序长度为 \(t\), 形成一个二维矩阵. 不同数据点的属性维度相同, 时序长度不同. 时序数据的数据点也是二维矩阵, 一维表示属性, 一维表示时间序列. 比如一段气象数据为一个数据点, 包含五种属性(温度, 湿度, 气压, 风速, 风向), 30分钟为一个时间序列, 每分钟采样依次, 则构成 \(5\times 30\) 的二维矩阵.
使用不同的 \(\mathbf{W}\) 可以提取到不同的特征, 这些不同的特征拼接起来可以得到一个新的维度(一维变二维, 二维变三维), 称为通道(channel). 一个典型的拥有通道的例子是RGB彩色图像(\(h\times w\times 3\)), 有三个通道, 而灰度图像可以看作二维图像或单通道的三维图像.
值得注意的是如果我们使用 \(\eqref{eq:affine}\) 提取特征, 那么我们需要把高维的数据展平成向量作为 \(\mathbf{x}\). 但这么做显然丢失了一些信息, 如图像邻近像素之间的关联关系, 时序数据中的先后关系. 因此我们需要其他手段提取数据的特征——卷积.
在数学中, 卷积是把两个算子(operator)/函数(function)合并为一个算子的操作, 一元函数 \(f\) 和 \(g\) 的连续卷积公式表达为:
\[(f\star g)(t) = \int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau.\]离散卷积类似, 把积分换为求和, 定义域变为离散点集:
\[(f\star g)(n) = \sum_{m=-\infty}^{\infty}f(m)g(n-m).\]卷积的操作可以看作固定函数 \(f(\cdot)\), 把函数 \(g(\cdot)\) 沿 \(x\) 轴翻转并平移 \(t\) 个单位后, 与 \(f(\cdot)\) 在重叠区域上求积再求和. 这里的求积即为两个函数相乘, 求和即为计算积分(连续)或求和(离散). 根据以上定义, 很容易把卷积推广到二元和多元函数上. 下表给出了几个简单地一维卷积和二维卷积的例子.
| 例子 | 记号 | 可视化 |
|---|---|---|
| 一维连续卷积 | \(f(\tau)=1,\;\tau\in[-0.5, 0.5]\) \(g(\tau)=\sqrt{r^2-\tau^2},\;\tau\in[-r, r]\) \(f\star g=\int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau\) |
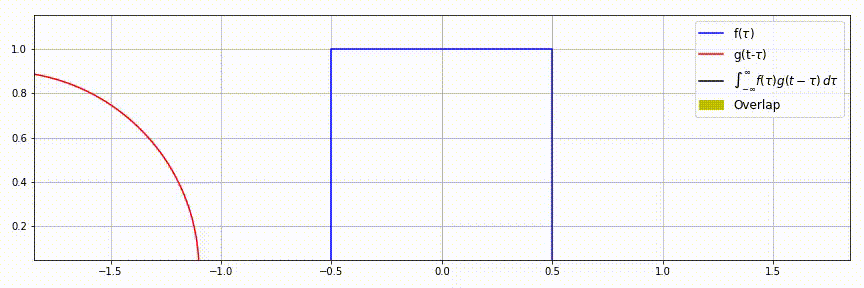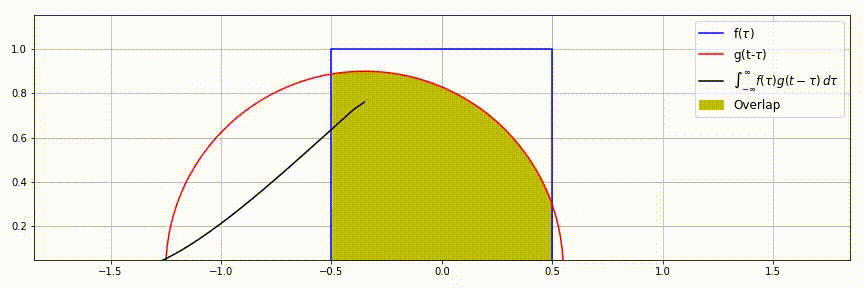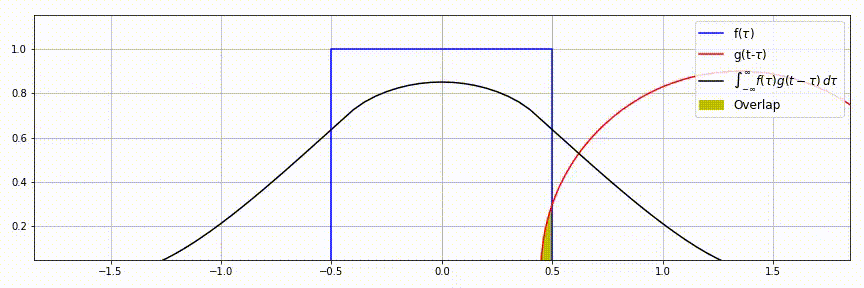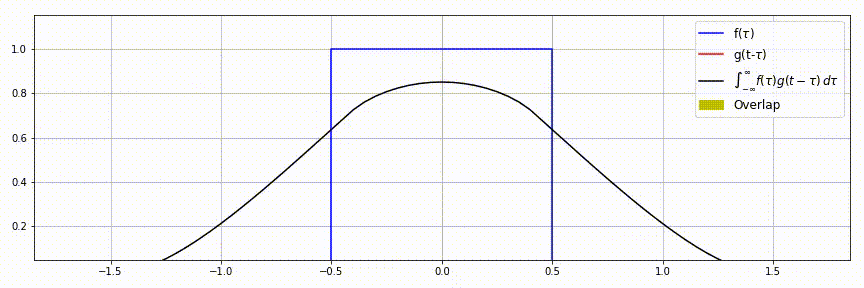 |
| 一维离散卷积 | \(f(m)=a_m, m\in\{0, 1, 2, 3, 4\}\) \(g(m)=w_m, m\in\{0, 1, 2\}\) \((f\star g)(n)\) |
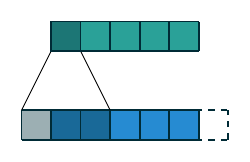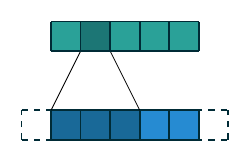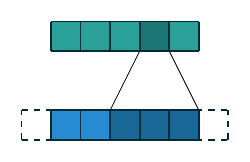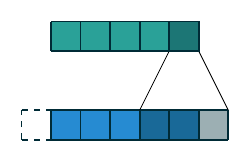 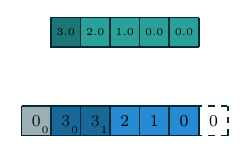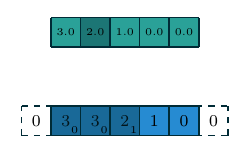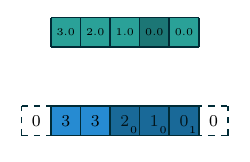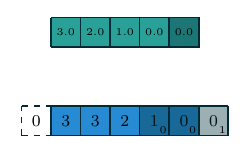 |
| 二维离散卷积 | \(f(m, n)=a_{m, n}, m, n\in\{0, 1, 2, 3, 4\}\) \(g(m, n)=w_{m, n}, m, n\in\{0, 1, 2\}\) \((f\star g)(n)\) |
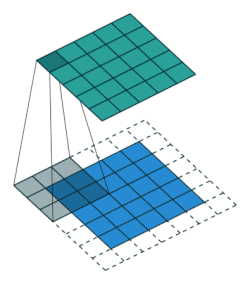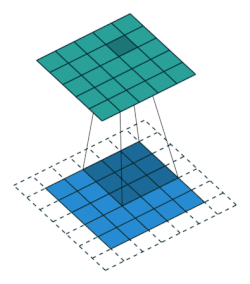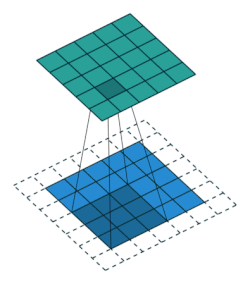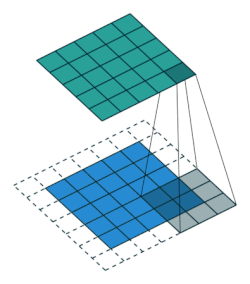 |
一维和二维离散卷积的例子如上表所示. 下面我们重点讨论二维离散卷积, 这也是在深度学习中使用最为广泛的卷积方式. 我们首先列出一些基本概念:
- 输入的特征图: 上表中的蓝色区域(仅显示了一个通道), 一般来说
shape=[h_in, w_in, c_in] - 卷积核: 上表中的阴影区域(仅显示了一个卷积核的一个通道), 一般来说
shape=[k, k, c_in, c_out] - 输出的特征图: 上表中的青色区域(仅显示了一个通道), 一般来说
shape=[h_out, w_out, c_out]
以及一些符号:
- \(i_j\) 输入特征图沿第 \(j\) 轴的尺寸(input)
- \(k_j\) 卷积核沿第 \(j\) 轴的尺寸(kernel)
- \(s_j\) 卷积操作沿第 \(j\) 轴的步长(stride)
- \(p_j\) 沿第 \(j\) 轴首和尾填充零的个数(padding)
- \(r_j\) 膨胀卷积的膨胀率(rate)
- \(o_j\) 输入特征图沿第 \(j\) 轴的尺寸(output)
第2章 卷积运算
为了讨论时能关注重要的问题, 我们约定下面的二维卷积中以上的参数沿着两个空间维度是相同的(即各向同). 同时我们默认填充均为零填充.
2.1 卷积
| 配置 | 目标 | 记号 | 可视化 |
|---|---|---|---|
| 无填充, 单位步长 | valid, \(p=0\) | \(p=0, s=1\) \(o=(i-k)+1\) |
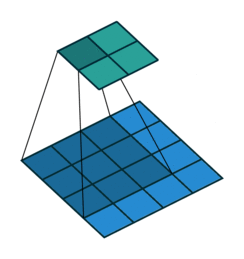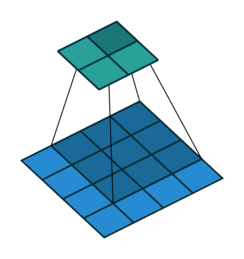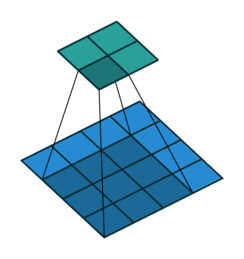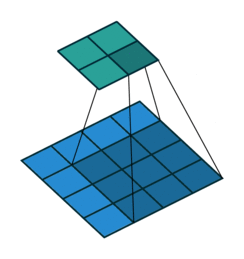 |
| 填充, 单位步长 | \(s=1\) \(o=(i-k)+2p+1\) |
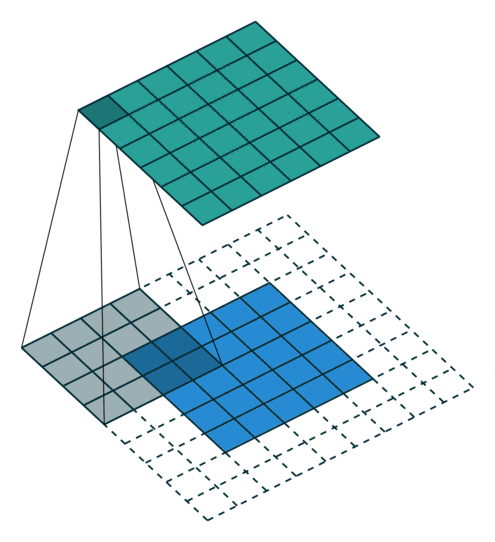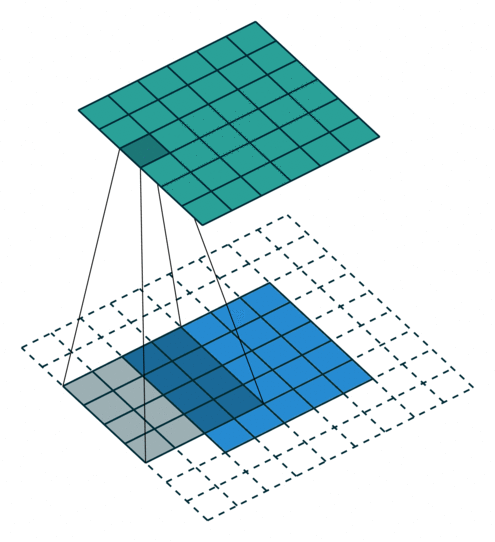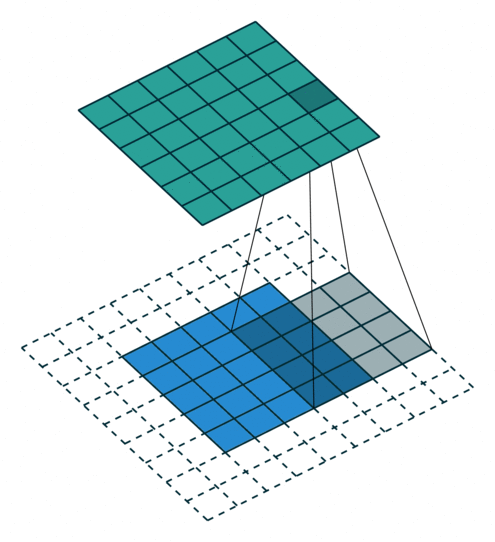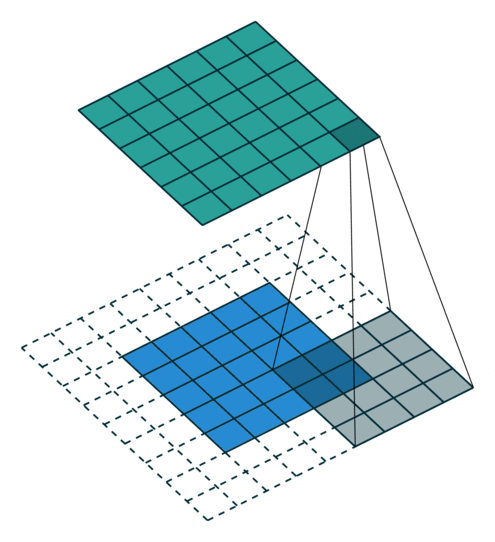 |
|
| 半填充(\(k\) 为奇数) 单位步长 |
same, \(o=i\) | \(p=\left\lfloor k/2\right\rfloor, s=1\) \(o=i\) |
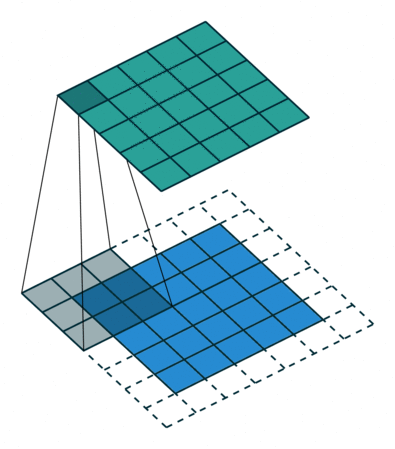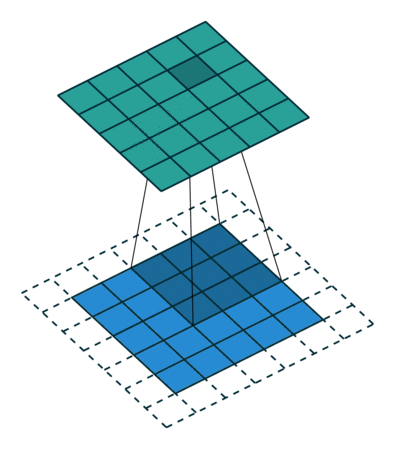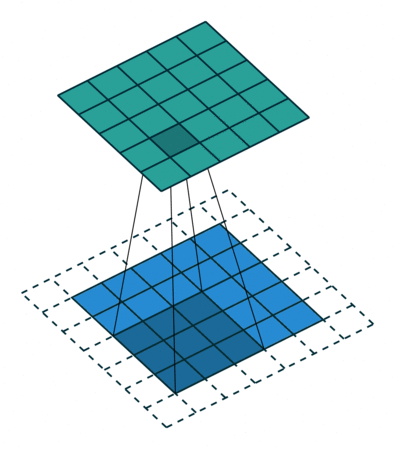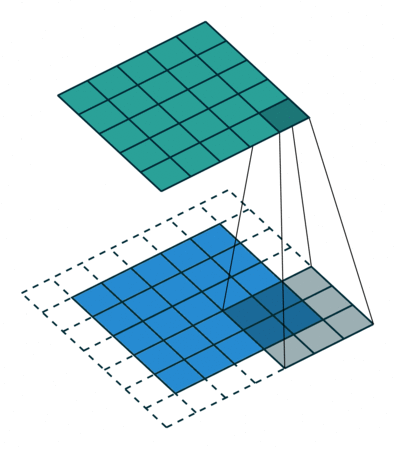 |
| 全填充, 单位步长 | full, \(o>i\) | \(p=k-1, s=1\) \(o=i+(k-1)\) |
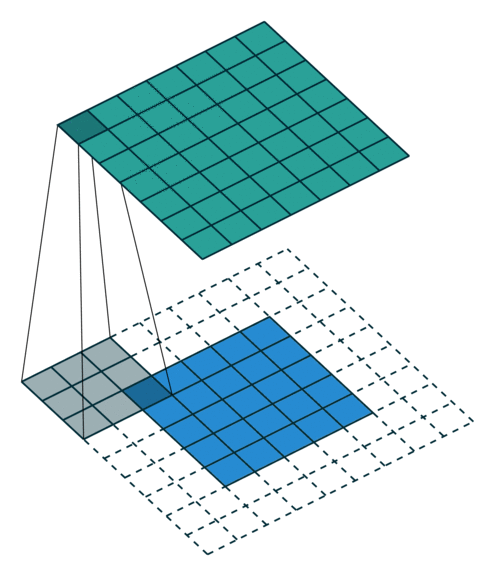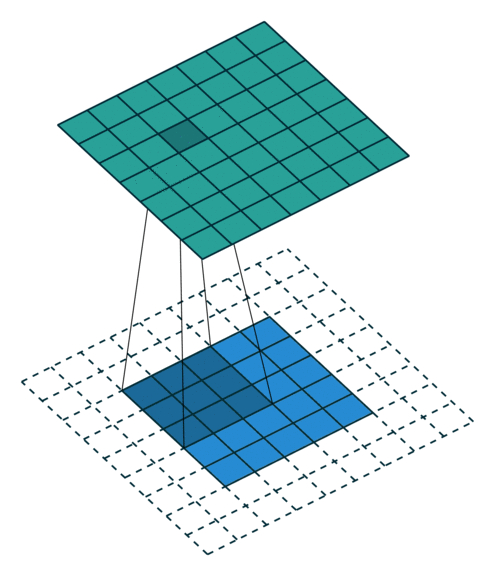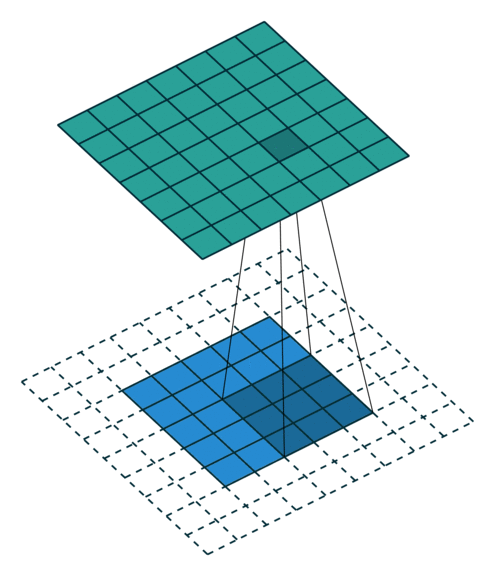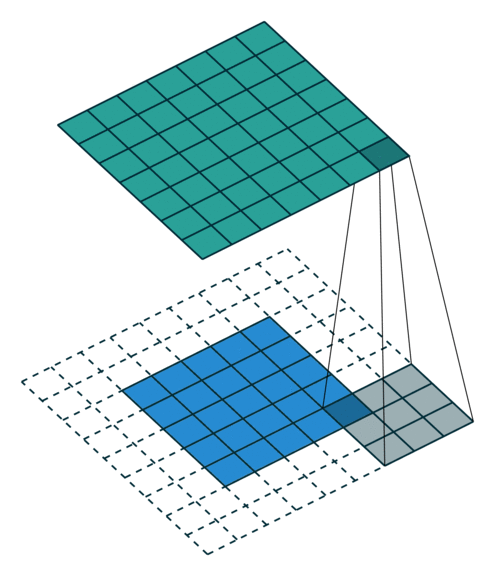 |
| 无填充, 非单位步长 | valid, \(p=0\) | \(p=0\) \(\displaystyle o=\left\lfloor\frac{i-k}{s}\right\rfloor+1\) |
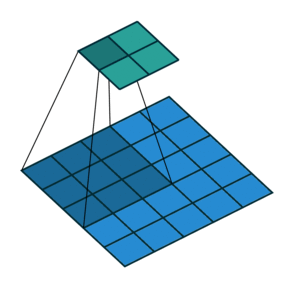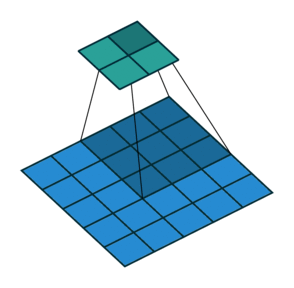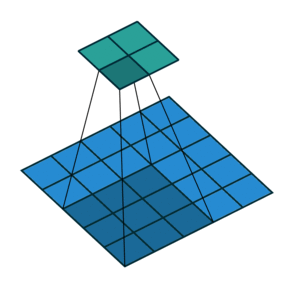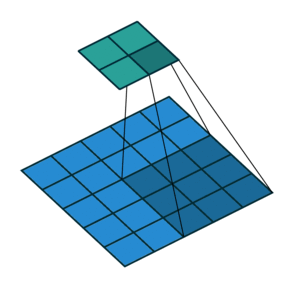 |
| 填充, 非单位步长 | \(\displaystyle o=\left\lfloor\frac{i+2p-k}{s}\right\rfloor+1\) | 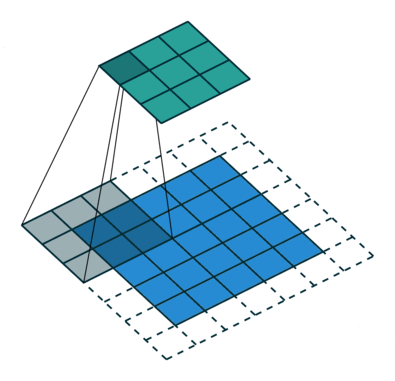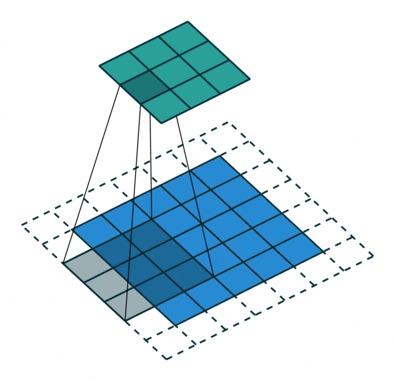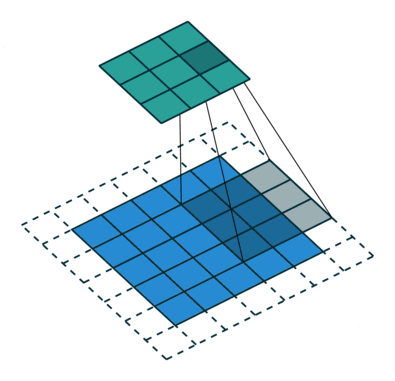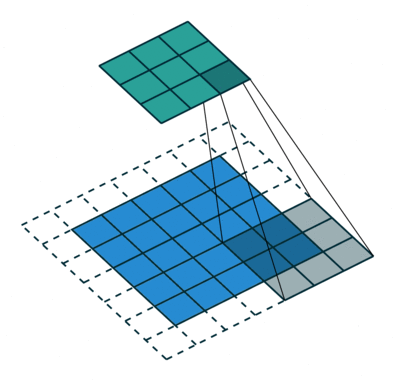 |
|
| 卷积核未覆盖 末行末列 |
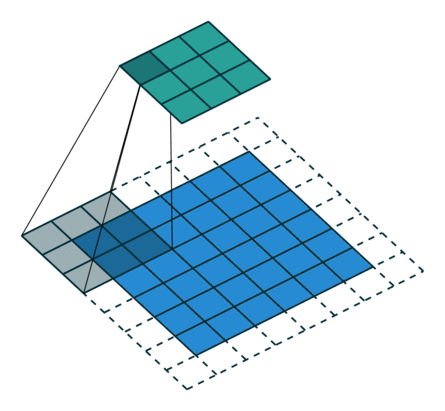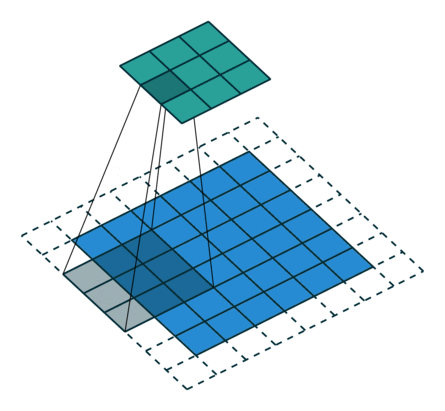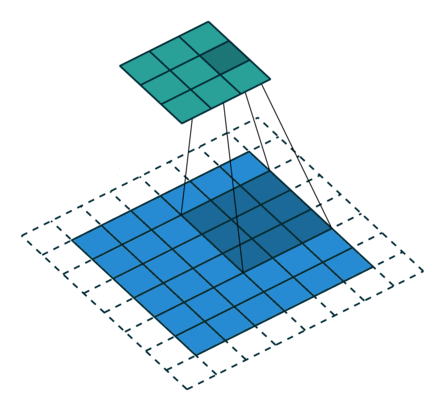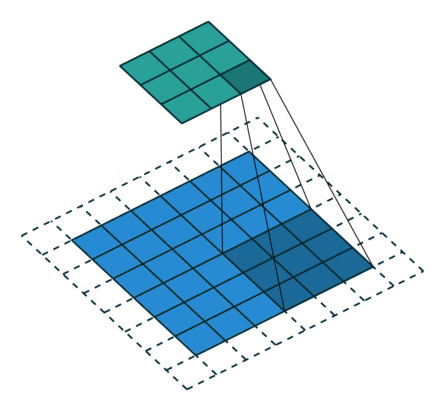 |
2.2 转置卷积
转置卷积的需求来源于我们有时候需要一个和卷积相反的过程, 即我们有时候需要根据输入的特征图, 产生特定大小的输出(如输出尺寸翻倍). 显然转置卷积仍然是一个算子, 因为它把特征图从输入空间映射到一个输出特征空间. 尽管我们可以使用如线性插值来完成尺寸翻倍的这类操作, 但卷积核仍然比插值算子有着可学习的(learnable)优势.
注意我们这里指的逆运算仅仅是指特征图的尺寸, 本文中不考虑值的逆运算.
对于全连接(fully connected, FC)运算来说, 矩阵 \(\mathbf{A}\in\mathbb{R}^{n\times 2n}\) 是一个算子, 把 \(\mathbb{R}^{2n}\) 中的向量映射到 \(\mathbb{R}^n\) 中, 这是一个特征压缩的过程. 其逆运算(特征数量翻倍)容易想到, 即左乘 \(\mathbf{A}^T\in\mathbb{R}^{2n\times n}\) 即可:
\[\mathbf{x} = \mathbf{A}^T\mathbf{y},\quad y\in\mathbb{R}^n, x\in\mathbb{R}^{2n}.\]对于卷积运算来说, 其逆运算就没FC这么显然, 但我们仍然可以借助于FC来理解下面表格里转置卷积的公式. 首先我们需要了解的一个事实是:
卷积操作可以看作矩阵向量乘法: 卷积核展平并填充零后形成算子矩阵, 特征图展平成一个向量.
下面的示意图展示了构造的过程核这种转换的关系.
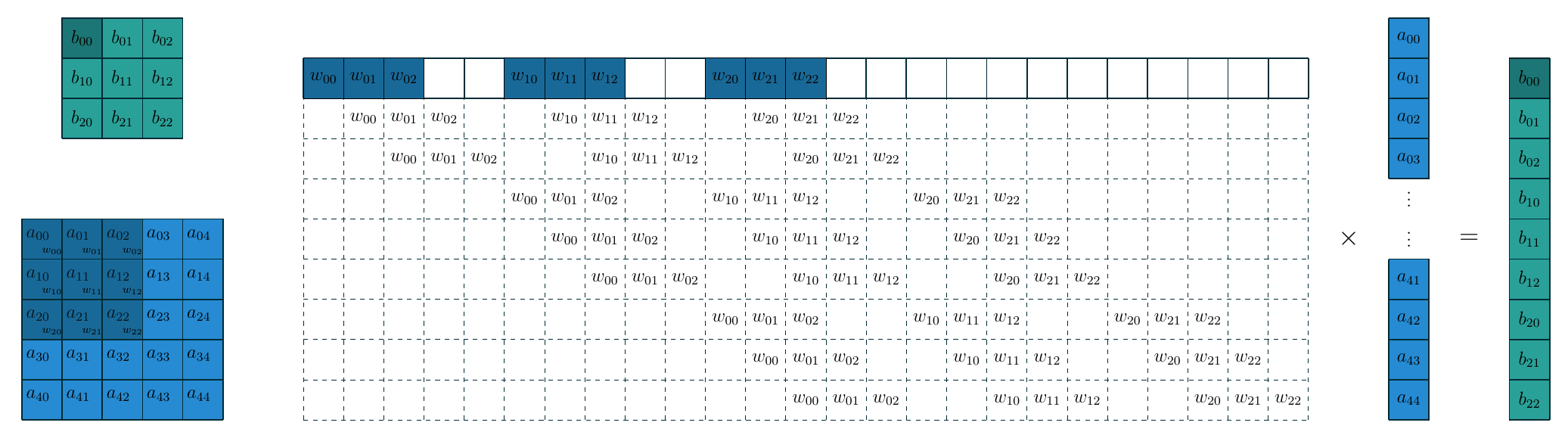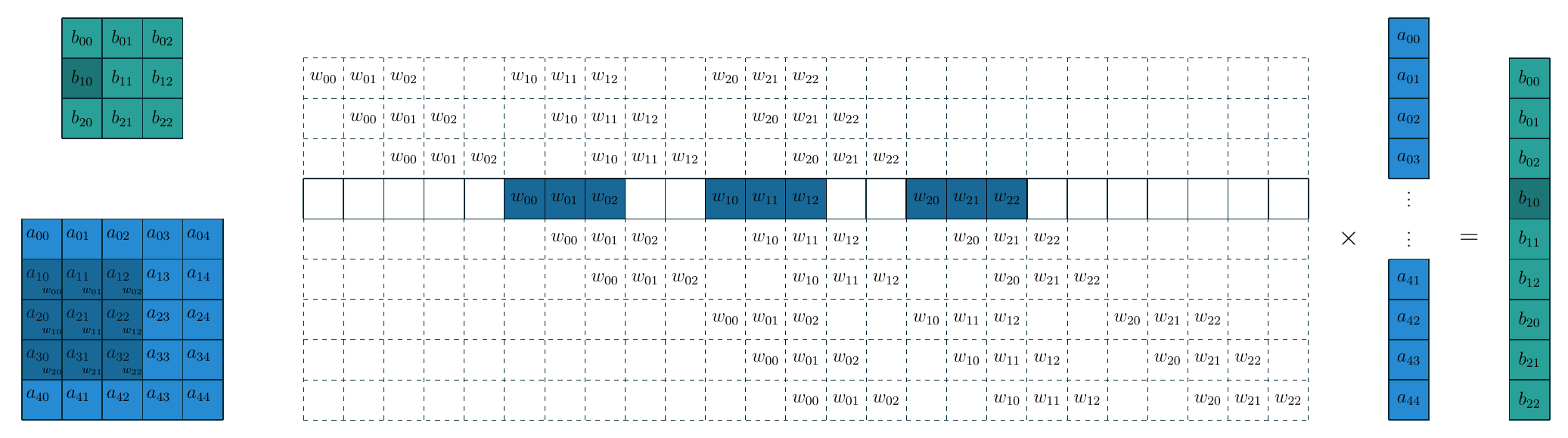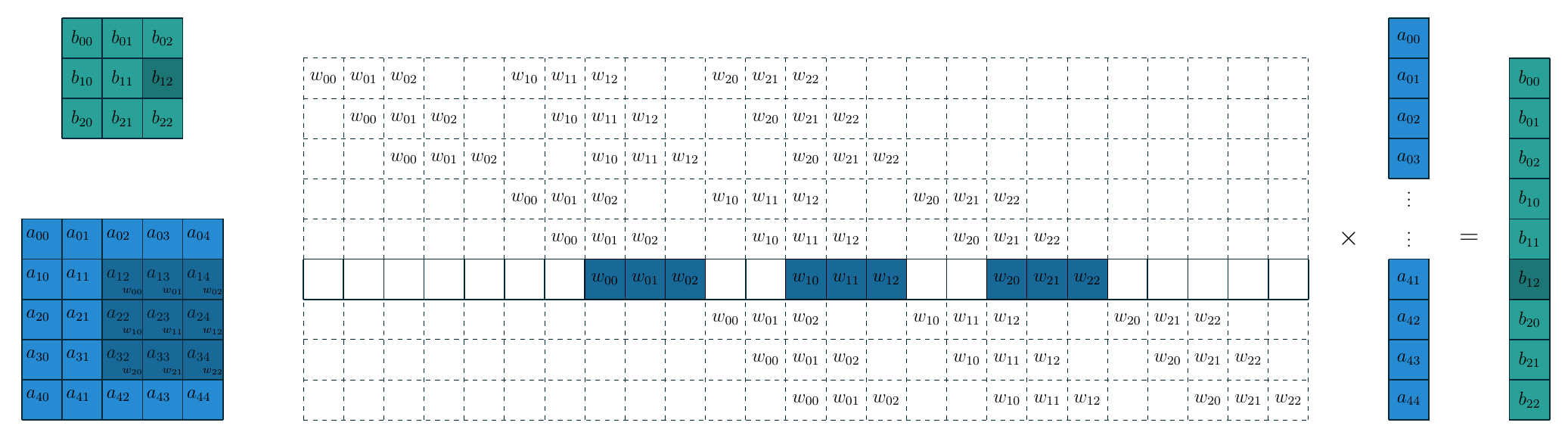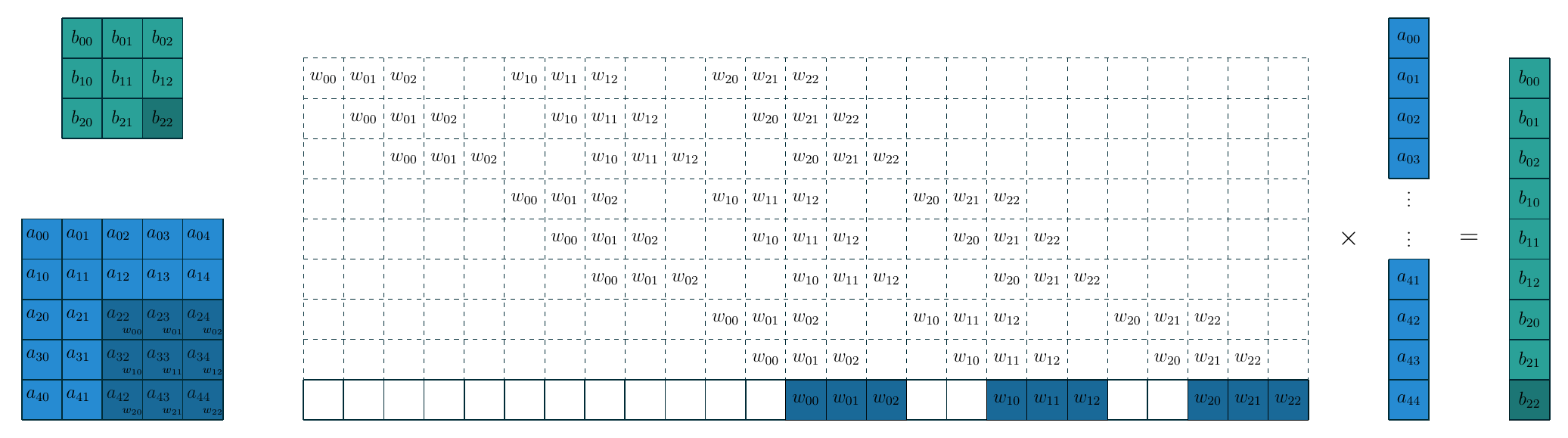
把卷积看作矩阵核向量的乘法运算之后, 转置卷积核FC的逆运算就完全一样了, 即把上图中间的大矩阵做一个转置即可, 此时转置卷积就是把 \(3\times3\) 的特征图映射为 \(5\times5\) 的特征图. 需要注意的是, 转置卷积本质上还是卷积, 只不过它在输入输出特征图的尺寸与某一个卷积互逆. 因此要完成卷积操作我们需要计算出相应的填充数, 步长, 同时对卷积核在水平和垂直方向翻转(即旋转180度). 在这个例子中, 填充数 \(p=2\), 步长 \(s=1\), 下面的示意图是上图对应的转置卷积.
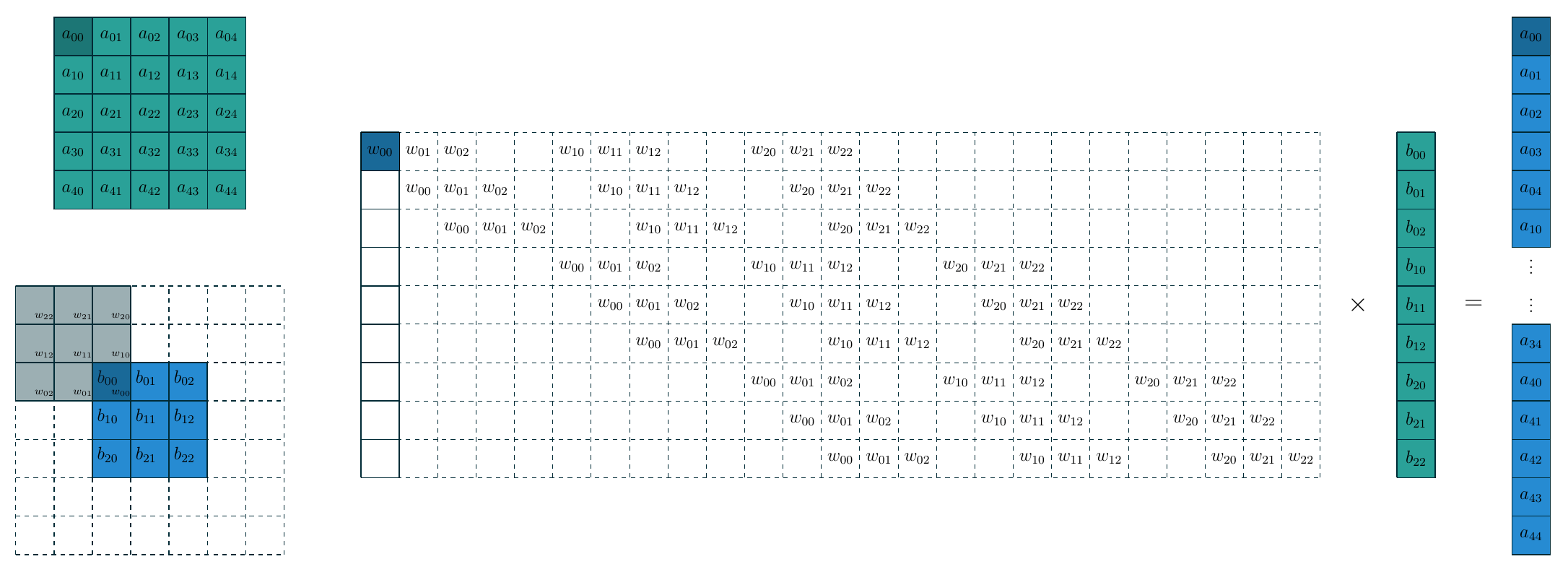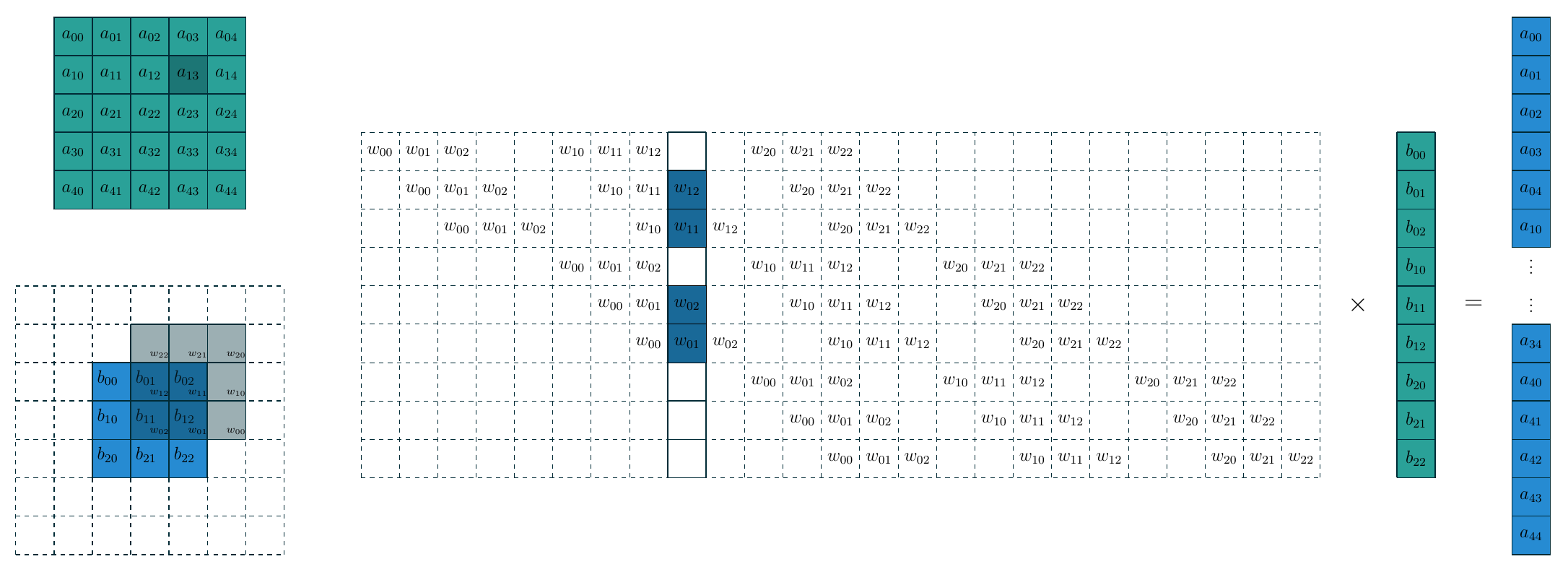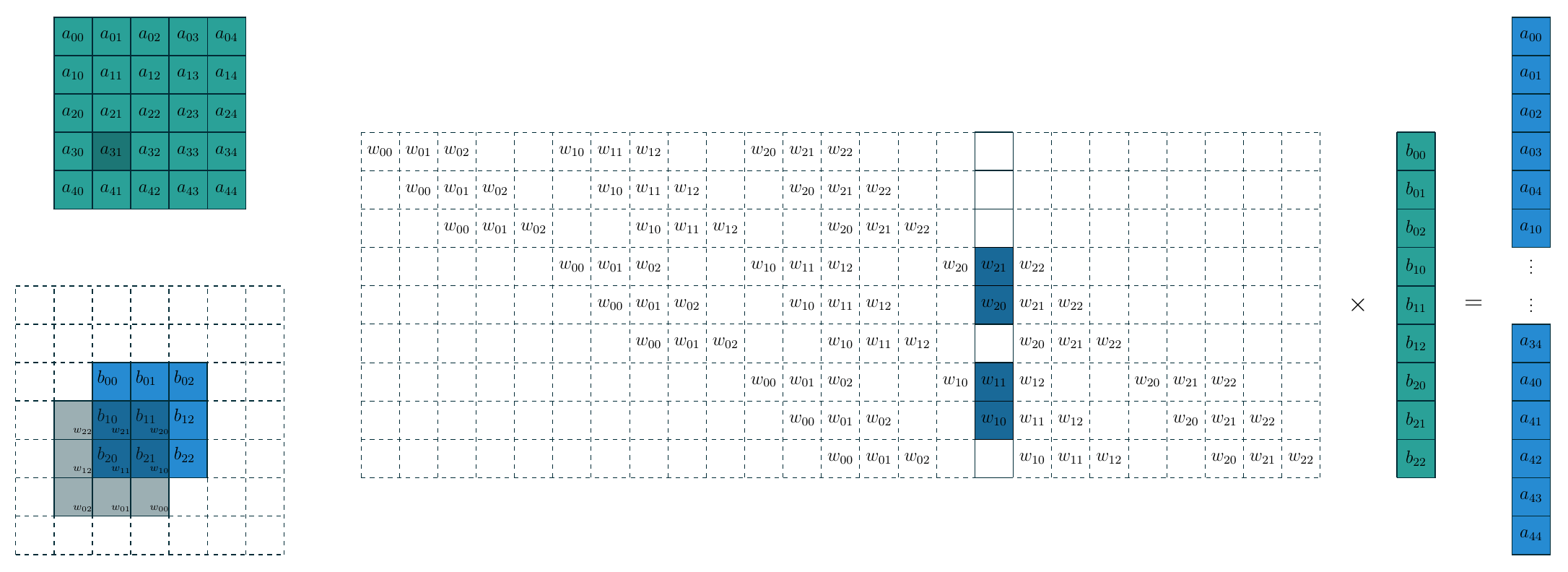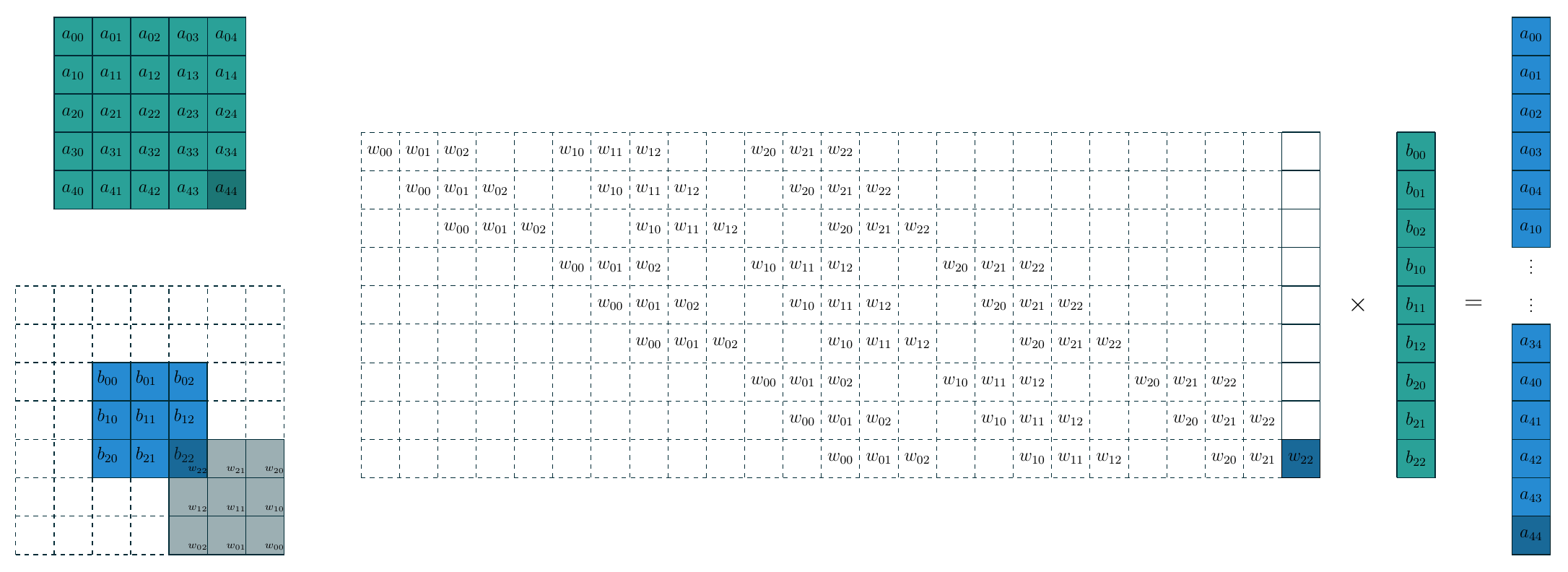
2.3 再看卷积
注意到我们在上面讨论的卷积看做矩阵乘法的提法会出现较大的卷积核构成的稀疏矩阵. 我们也可以把特征图进行展开, 从而可以形成一个稠密的向量. 这个过程在现在深度学习框架中称为 im2col. 其具体操作过程是: 把卷积核看做掩模矩阵, 按照既定规则在特征图上进行滑窗, 把每次掩模矩阵覆盖的特征图的矩形区域展成向量; 然后把所有的向量组成一个新的矩阵; 最后用这个新的矩阵与卷积核执行矩阵乘法. 如下图所示.
动图生成
本文动图生成的代码见 Github.
生成方式:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 在 Ubuntu 下, 预先安装 apt install ImageMagick 用于格式转换
# 测试安装是否成功
# convert -h
# 安装 Latex 软件, 这里的代码需要 pdflatex 引擎
# 进入项目目录
cd jarvis73.github.io/code/conv_arithmetic
# 1. 首先生成逐帧的pdf
# 卷积
# python ./code/20190606-Conv.py conv
# 反卷积
# python ./code/20190606-Conv.py conv_transpose
# 另一种卷积的展开方式(框架里的用法)
python ./20190606-Conv.py conv_v2
# 2. pdf 转 png
bash ./pdf2png.sh 201906_conv_v2
# 3. 合并 png 为 gif
convert -delay 60 201906_conv_v2_png/*.png output.gif
参考文献
-
Gradient-based learning applied to document recognition
Yann LeCun, Lon Bottou, Yoshua Bengio, Patrick Haffner.
[link]. In Proceedings of the IEEE[J], 1998, 86(11): 2278-2324. ↩ -
Imagenet classification with deep convolutional neural networks
Krizhevsky A, Sutskever I, Hinton G E.
[link]. In NIPS[C] 2012: 1097-1105. ↩ -
A guide to convolution arithmetic for deep learning
Vincent Dumoulin, Francesco Visin
[link]. In arXiv: abs/1603.07285 ↩