在二分类任务中, 标准的分类技术通常要同时使用正样本和负样本进行训练, 在本章的生成式模型中, 我们主要探讨如何单独从正样本中学习. 比如我提出一个概念(但是我保密), 同时我给出一些符合这个概念的例子(正样本), 你如何猜出这个概念(数据分布).
举个例子: 假设我们的样本空间是 1 到 100, 并且我给出一个正样本 16, 那么你猜我所提出的概念是什么? 偶数? 2 的 n 次幂? 小于 50 的数? 我们可以看到有太多种猜测的结果, 但实际上我们对每种猜的结果的倾向性是不同的, 比如也许会更倾向于 2 的 n 次幂. 当我再给出一个数字 64, 你是否会更加肯定这种倾向? 同时虽然 {16, 64} 都是偶数, 但是也许你对 2 的 n 次幂的倾向性会更大. 那么这种倾向性如何衡量? 下面会给出进一步的答案.
此外, 本章我们仅考虑离散数据.
1. 贝叶斯概念学习
通俗的说, 贝叶斯概念学习就是从一个集合的样本中学习出一般的概念. 比如我们前言中的例子, 给出集合 \(\mathcal{D}=\{16, 8, 2, 64\}\), 我们可以比较肯定得说这个集合背后的”概念”是 2的幂, 而不太倾向于说是偶数.
1.1 似然
为了解释这个原因, 我们引入似然的概念(或称为似然函数):
定义: 令 \(X\) 是一个离散随机变量, 概率密度函数 \(p\) 依赖于参数 \(\theta\) , 那么函数 \(\mathcal{L}(\theta\lvert x)=p_{\theta}(x)=P_{\theta}(X=x),\) 是参数 \(\theta\) 的函数, 称为给定 \(x\) 下 \(\theta\) 的似然函数(likelihood function).
这里要注意似然和概率的区别.
- 概率: 指的是概率空间中某个事件发生的概率, 是关于联合样本 \(\mathbf{x}\) 的函数
- 似然: 指的是联合样本 \(\mathbf{x}\) 关于未知参数 \(\theta\) 的似然, 是关于参数 \(\theta\) 的函数
此外, 我们还需要引入一个法则:
奥卡姆剃刀(Occam’s Razor): 如无必要, 勿增实体, 即”简单有效原理”.
在这样的法则下, 我们可以假设抽取集合 \(\mathcal{D}\) 时是简单随机抽样, 并且每个元素被抽到的概率相等(即均匀分布), 那么从满足”概念” \(h\) 的集合中抽取到集合 \(\mathcal{D}\) 的概率就是可计算的
\[p(\mathcal{D}\lvert h)=\left[\frac{1}{size(h)}\right]^{size(\mathcal{D})}.\]现在我们可以计算一下上面的例子. 2 的幂次的集合为 \(h_{powers~of~2}\triangleq\{1,2,4,8,16,32,64\}\), 而偶数的集合为 \(h_{even}\triangleq\{2,4,6,\dots,100\}\). 从而 \(p(\mathcal{D}\lvert h_{povers~of~2})=(1/7)^4=4.2\times10^{-4}\), 而 \(p(\mathcal{D}\lvert h_{even})=(1/50)^4=1.6\times10^{-7}\). 显然认为这个”概念”是 2 的幂时能够抽取到集合 \(\mathcal{D}\) 的概率更大, 那么我们也更倾向于相信这种猜测. 同时我们也能得到给定集合 \(\mathcal{D}\) 时参数 \(h_{powers~of~2}\) 的似然要远大于 \(h_{even}\) 的似然.
1.2 先验和后验
定义: 在贝叶斯统计学中, 一个不确定量的先验概率分布(也称为先验)指的是在”观测到数据”之前, 我们对于这个未知量不确定性的一种估计.
一个直观的例子就是我们在1.1节中每种假设下, 该假设集合中的每个元素被抽到的概率相等, 那么这里的先验分布就是一个均匀分布.
定义: 后验概率分布(也称为后验)则指的是在给出”观测数据”之后, 对于未知量的条件概率分布. 其表达式为
\[p(h\lvert\mathcal{D})=\frac{p(\mathcal{D}\lvert h)p(h)}{\sum_{h'\in\mathcal{H}}p(\mathcal{D}, h')}\]其中 \(p(h\lvert\mathcal{D})\) 为后验概率, \(p(\mathcal{D}\lvert h)\) 为似然, \(p(h)\) 为先验概率.
后验概率可以解释为先验概率和似然经过正则化的乘积. 为了说明先验, 后验和似然的关系, 我们仍然用上面的例子 —- “猜概念”. 首先我们给出30种不同的先验: 偶数的集合, 奇数的集合, 以 6 结尾的数…等. 再考虑”观测数据”的集合 \(\mathcal{D}=\{16, 8, 2, 64\}\), 下面两幅图给出了先验概率, 似然和后验概率的结果:
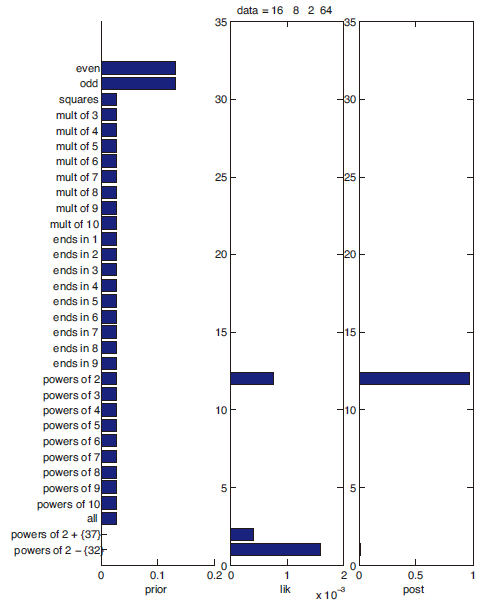
先验/似然/后验
下面对上图做一些评论:
- “奇数”和”偶数”这两个猜想的先验概率很高, “2 的幂加上 {37}”和”2 的幂减去 {32}”这两个猜想先验概率很低
- 当出现观测值 \(\mathcal{D}\) 时, 绝大部分猜想由于与观测值相悖(如: “奇数”)而似然为 0; 而有一些猜想的似然很高(如: “2 的幂次”, “2 的幂次减去 {32}”等), 有一些猜想的似然很低(如: “偶数” 接近 0) .
- 后验概率为第三列, 可以发现两个似然很高的特殊情况”2 的幂次加上 {37}”和”2 的幂次减去 {32}”由于先验很低, 所以最终的后验概率也极低. 而”2 的幂次”这个猜想获得了最高的后验概率.
从上面的几点评论中我们进一步证实了为什么见到观测数据 \(\mathcal{D}=\{16,8,2,64 \}\) 后我们更倾向于认为原始猜想是”2 的幂次”而非”偶数”了.
1.3 MLE 和 MAP
这一小节主要理清最大似然估计(maximum likelihood estimation, MLE), 最大后验概率(maximum a posterior probability estimation, MAP)的概念和关系. 这二者都是数理统计中参数估计的方法. 根据前面似然函数的知识, \(MLE=\text{argmax}_{h}p(\mathcal{D}\lvert h)\). 而最大后验概率 \(MAP=\text{argmax}_hp(\mathcal{D}\lvert h)p(h)\). 可以发现二者仅相差一个 \(p(h)\) , 其含义便有所区别:
- MLE 是寻找一个 \(h\) 使得数据集 \(\mathcal{D}\) 出现的概率最大
- MAP 是我们(主观的)给出事件的一个先验概率后, 寻找一个 \(h\) 使得数据集 \(\mathcal{D}\) 出现的概率最大
这二者的区别主要是由先验概率决定的, 实际上我们可以把 MLE 的先验看作均匀分布, 这也是一个直观的解释: 当我们对数据分布一无所知时, 那么均匀分布就是最好的先验分布.
1.4 后验预测分布
当我们知道了什么是似然, 什么是先验分布和后验分布, 那我们接下来就该考虑一个更实际的二分类问题:
假设我们从数据空间已经获取了一批带标注的数据集 \(\mathcal{D}\), 当给出一个新的数据点 \(\tilde{x}\) 时, 如何估计该数据点的类别?
- 法一(基于规则的推理 rule-based reasoning): 最直接的想法就是使用数据集 \(\mathcal{D}\) 估计该数据集分布的最优参数 \(\theta\) , 然后自然根据参数就能得到新数据点 \(\tilde{x}\) 的预测值.
法一最大的优势在于简单, 容易实现. 根据数据集估计最优参数, 那么这其实就是求极大似然估计MLE的过程. 并且把这种使用单一参数值作进行估计的方法称为插入近似(plug-in approximation). 同时, 这个”最优参数”就是所谓的规则. 根据描述, 我们容易得到 \(\tilde{x}\) 的后验预测分布(定义见下文)为
\[p(\tilde{x}=1\lvert\mathcal{D})= p(\tilde{x}\lvert\theta_{MLE})\]法一虽然简单, 但是它完全忽视了数据的不确定性. 换句话说就是数据集 \(\mathcal{D}\) 的分布可能并不完全和数据空间相同, 因为采样是存在偏差的. 仅估计一个单一的 \(\theta\) 值就忽视了偏差的存在, 即忽视了数据采样的不确定性, 因此我们提出法二.
- 法二(基于相似度的推理 similarity-based reasoning): 不把 \(\theta\) 固定为一个值, 而是使用概率分布, 即 \(\theta\) 以不同的概率取不同的值. 离散形式如下式
连续形式为
\[p(\tilde{x}=1\lvert\mathcal{D})=\int_{\Theta}p(x=1\lvert\theta)p(\theta\lvert\mathcal{D})\,d\theta.\]上面两式称为后验预测分布, 它实际上是不同参数假设下数据分布的加权平均, 也称为贝叶斯模型平均(bayes model averaging, BMA), 显然它把不确定性考虑在内了. 哪个估计的参数值越接近真实参数值, 那么可以想象它所对应的概率也越大, 这就是相似度的含义.
- 特点: 可以发现当已观测到的数据集 \(\mathcal{D}\) 非常小时, 使用插入近似的后验预测分布会变得很窄(即过拟合了); 增大数据集 \(\mathcal{D}\) 时, 后验预测分布会逐渐变宽(增加数据减轻过拟合). 使用贝叶斯模型平均方法则后验预测分布会从宽变窄. 而当数据量不断增大, 两种方法最终会收敛到相同的结果.
下面仍然考虑上面的例子, 数据空间为[1, 100]. (因为仅考虑离散数据)我们给定如下不同的先验:
- 奇数
- 偶数
- 平方数
- 3 的倍数, 4的倍数, …, 10 的倍数
- 以 1 结尾, 以 2 结尾, …, 以 9 结尾
- 2 的幂次, 3 的幂次, …, 10 的幂次
- 所有数据
- 2 的幂次去掉 37
- 2 的幂次 添上 32
| 数据集 | \(\mathcal{D}=\{16\}\) | \(\mathcal{D}=\{16, 8, 2, 64\}\) |
|---|---|---|
| 插入近似 | (窄) 4 的幂次似然最大, 图 1 | (宽) 2 的幂次似然最大, 图 2 |
| 贝叶斯模型平均 | (宽) | (窄) |
[注:] 下次画几张图
2. 补充
过拟合和黑天鹅悖论
在1.4节提到插入法得到的后验预测分布过窄, 这其实是过拟合, 维基百科定义如下
定义: 在统计学中, 过拟合是对一组数据分析得过于恰好的结果, 以至于可能会无法拟合额外的数据或无法对未来做出可靠的预测.
在另外一些定义中, 可能会提到使用”过多的参数”导致的过拟合, 维基百科的这个定义是更加”一般化”的说法. 比如数据量过少时插入法得到的后验预测分布就很容易产生过拟合, 但这种过拟合并不是参数过多导致的, 而是选择了个”过于恰好”的模型.
似然/先验/后验举例
参考 Machine Learning: A Probabilistic Perspective, by Kevin P. Murphy 第三章
- 3.3 The beta-binomial model
- 3.4 The Dirichlet-multinomial model
