扩散模型 DDPM 尽管生成效果不错, 但采样速度相比 GAN 要慢很多. GAN 采样只需要一次神经网络前馈, 而 DDPM 需要 \(T\) 步前馈, \(T\) 的典型取值为 1000. 因此 Nichol and Dhariwal 在 《Improved Denoising Diffusion Probabilistic Models》 提出 improved DDPM, Song 等人在 《Denoising Diffusion Implicit Models》 中提出 DDIM 用于加速扩散模型的采样.
改进 DDPM
DDPM 训练出来的扩散模型虽然其生成效果不错, 但由于对数似然相比于 GAN 等模型不够好, 因此其生成的多样性也会打一个折扣, 即原文中所说的 \(\newcommand{\xx}{\bm{x}} \newcommand{\pt}{p_{\theta}} \newcommand{\mt}{\bm{\mu}_{\theta}} \newcommand{\st}{\bm{\Sigma}_{\theta}}\)
Log-likelihood is a widely used metric in generative modeling, and it is generally believed that optimizing log-likelihood foces generative models to capture all of the modes of the data distribution (Razavi et al. 2019).
那么如何改进对数似然呢? Improved DDPM 给出了如下一些改进:
学习 \(\Sigma_{\bm\theta}(\xx_t,t)\)
DDPM 中把反向过程的协方差矩阵定义为对角矩阵 \(\Sigma_{\bm{\theta}}(\xx_t,t)=\sigma_t^2\bm{I}\), 这里的 \(\sigma_t^2\) 是固定住的. 并且探讨了 \(\sigma_t^2\) 取两种极端情况 \(\sigma_t^2=\beta_t\) 和 \(\sigma_t^2=\tilde{\beta}_t=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\beta_t\) 下的模型表现差不多.
Improved DDPM 一文中指出虽然 \(\sigma_t^2\) 的取值对于生成表现差不多, 但不代表对对数似然没影响, 并且通过实验说明了训练前期选择合适的 \(\sigma_t^2\) 确实是有利于对数似然的提升的(对应地降低似然损失). 因此提出学习一组方差:
\[\Sigma_{\bm\theta}(\xx_t,t) =\exp(v\log\beta_t+(1-v)\log\tilde{\beta}_t)\]为了更容易的优化, 直接学一组参数 \(v\), 然后对 \(\beta_t\) 和 \(\tilde{\beta}_t\) 插值得到方差.
此外, 由于简化的 DDPM 损失 \(L_{\text{simple}}\) 不依赖于 \(\Sigma_{\bm\theta}(\xx_t,t)\), 因此采样混合损失来同时优化方差项:
\[L_{\text{hybrid}} = L_{\text{simple}} + \lambda L_{\text{vlb}}\]其中 \(L_{\text{vlb}}\) 就是未简化版的变分下界损失, 见 \eqref{eq:ddpm_loss} 式. \(\lambda=0.001\) 保证 vlb 损失的影响不要太大影响了 simple 损失.
加噪方案
DDPM 采用的是线性的加噪方案 (linear schedule). Improved DDPM 提出了余弦方案 (cosine schedule):
\[\beta_t = \min\left(1-\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}, 0.999\right), \quad \bar{\alpha}_t=\frac{f(t)}{f(0)}, \quad f(t)=\cos\left(\frac{t/T+s}{1+s}\cdot\frac{\pi}2\right)^2\]其中加一个小的偏移 \(s=0.008\approx \frac1{127.5}\) 可以让 \(\beta_t\) 在 \(t=0\) 的时候不至于太小, 因为太小的话模型没办法预测准 \(\bm\epsilon\); 余弦函数可以使得 \(\beta_t\) 在接近 \(t=0\) 和 \(t=T\) 的时候变化缓慢一点, 生成效果更稳定.
线性方案和余弦方案的 \(\bar{\alpha}_t\) 的示意图如下:
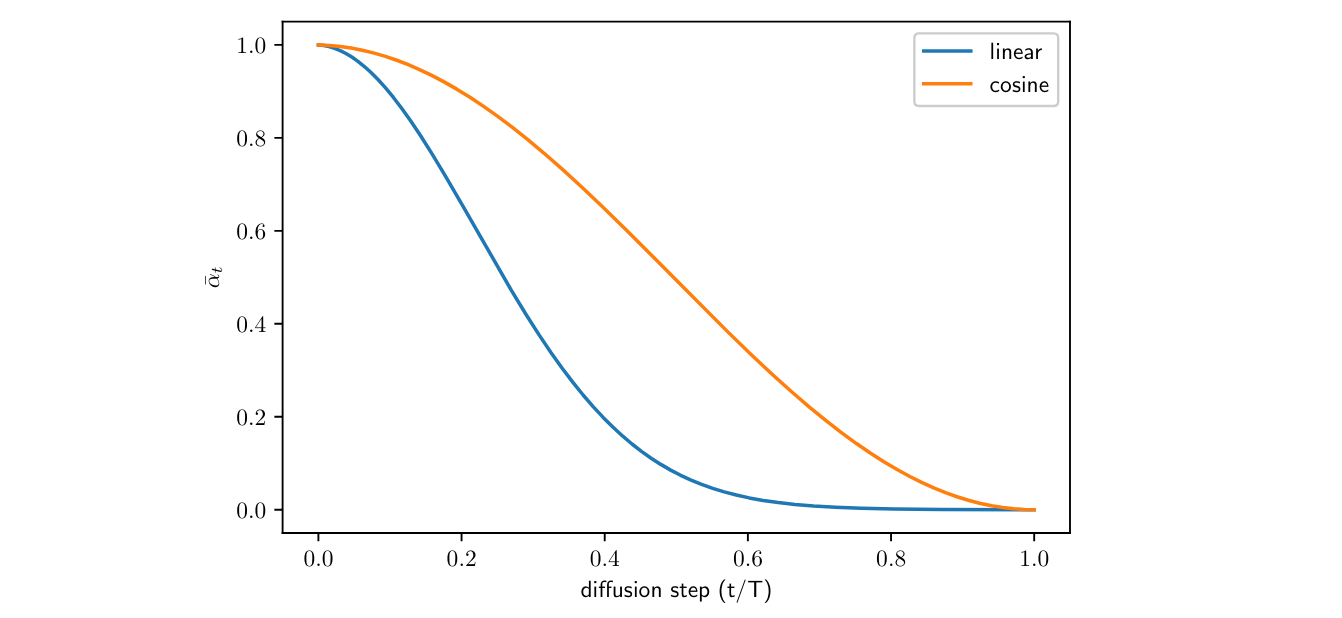
图 1. 加噪的线性方案和余弦方案
降低梯度噪声
理论上直接优化 \(L_{\text{vlb}}\) 可以获得更好地对数似然, 但 Improved DDPM 的作者发现直接优化比较困难, 并发现梯度噪声很大, 因此需要控制梯度的方差小一点.
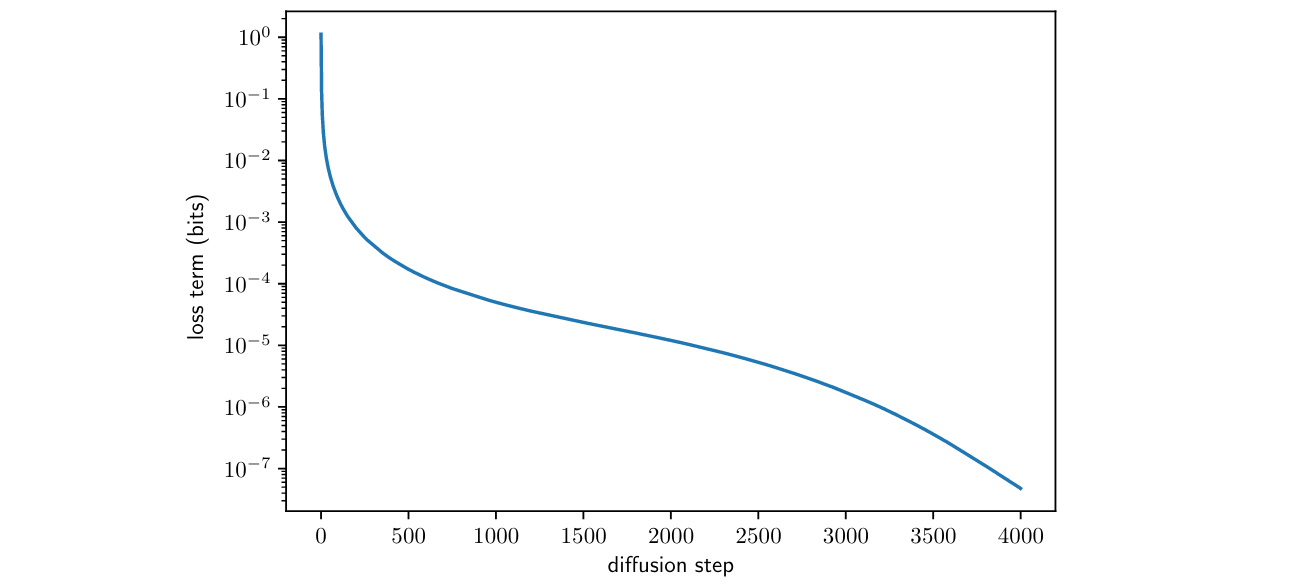
图 2. 扩散时间步和 VLB 的关系. 初始时间贡献了最多的负对数似然损失
作者猜测是因为时间步 \(t\) 均匀采样导致的梯度噪声大 (因为不同时间步的损失项差别很大, 如上图), 所以提出了时间步重要性采样的方法:
\[L_{\text{vlb}} = E_{t\sim p_t}\left[\frac{L_t}{p_t}\right],\quad p_t\propto\sqrt{E[L_t^2]}, \quad \sum p_t=1.\]由于 \(E[L_t^2]\) 无法获取准确值, 所以保存每个时间步前 10 次的损失求平均来估计, 这样损失越大的时间步采样频率越低, 从而整体上可以保证损失的稳定性.
使用重要性采样单独训练 \(L_{\text{vlb}}\) 确实有效, 损失也更稳定了. 直接训练 \(L_{\text{hybrid}}\) 的损失也可以降到和使用重要性采样的 \(L_{\text{vlb}}\) 差不多, 损失曲线稍微不稳定一点, 所以可以自由选择.
DDIM
DDIM 有两个主要的贡献, 一是扩散模型的前向过程可以是个非马尔科夫过程 (non-markovian process), 二是扩散模型可以通过子序列加速采样.
非马尔科夫链前向过程
回顾 DDPM 的损失函数,
\[\label{eq:loss} L_{\text{simple}}(\theta) \triangleq \mathbb{E}_{t,q(\xx_0),\bm{\epsilon}\sim\mathcal{N}(\bm{0},\bm{I})}\left[\Vert \bm{\epsilon} - \bm{\epsilon}_{\theta}(\xx_t,t) \Vert^2_2\right]\]其中 \(\xx_t=\sqrt{\bar{\alpha}_t}\xx_0 + \sqrt{\bar{\beta}_t}\bm{\epsilon}\), 也即 \(q(\xx_t\vert\xx_0) = \mathcal{N}(\xx_t;\sqrt{\bar{\alpha}_t}\xx_0, \bar{\beta}_t\bm{I})\), 其中 \(\bar{\alpha}_t+\bar{\beta}_t=1\). 由此我们可以发现, 训练 DDPM 时实际上只用到了边际分布 \(q(\xx_t\vert\xx_0)\) 而并没有用到联合分布 \(q(\xx_{1:T}\vert\xx_0)\), 这就意味着, 实际上只要边际分布的形式不变, 我们可以假定任意的联合分布的形式. DDPM 中把联合分布定义为马尔科夫链, 那么当然我们也可以把联合分布定义为非马尔科夫链的形式, 只需要保证边际分布一样, 那么就可以用相同的损失函数训练出相同的生成模型 (注意这里使用 “生成”, 因为严格来说不是马尔科夫链的话, 可能就不是”扩散”模型了).
如下图所示, 左边是马尔科夫形式的扩散生成模型, 右边是非马尔科夫形式的生成模型, 因为前向过程中 \(\xx_2\) 同时依赖 \(\xx_1\) 和 \(\xx_0\), 类似地 \(\xx_3\) 同时依赖 \(\xx_2\) 和 \(\xx_0\).

图 3. 马尔科夫形式的扩散生成模型和非马尔科夫形式的生成模型
举例: 全都依赖 \(\xx_0\)
DDIM 论文特别考虑了所有的 \(\xx_t,\;t=1,\cdots,T\) 都依赖于 \(\xx_0\) 的情况 (显然这是非马尔科夫的一种情况):
\[q(\xx_{1:T}\vert\xx_0)=q(\xx_T\vert\xx_0)\prod_{t=2}^Tq(\xx_{t-1}\vert\xx_t,\xx_0).\]按前文所述, 我们希望它满足边际分布的要求 \(q(\xx_t\vert\xx_0) = \mathcal{N}(\xx_t;\sqrt{\bar{\alpha}_t}\xx_0, \bar{\beta}_t\bm{I}),\;t=1,\cdots,T\), 因此我们需要定义出满足该边际分布的 \(q(\xx_{t-1}\vert\xx_t,\xx_0)\). DDIM 一文中定义了最后一项 \(q(\xx_T\vert\xx_0) = \mathcal{N}(\xx_T;\sqrt{\bar{\alpha}_T}\xx_0, \bar{\beta}_T\bm{I})\), 然后定义了递推项,
\[\label{eq:q_ditui} q(\xx_{t-1}\vert\xx_t,\xx_0) = \mathcal{N}\left(\sqrt{\bar{\alpha}_{t-1}}\underline{\xx_0}+\sqrt{1-\bar{\alpha}_{t-1}-\sigma_t^2}\cdot\underline{\frac{\xx_t-\sqrt{\bar{\alpha}_t}\xx_0}{\sqrt{1-\bar{\alpha}_t}}},\sigma_t^2\bm{I}\right)\]接下来在附录中使用归纳法证明了这样的定义可以使得对于所有的 \(t=1,\cdots,T-1\) 都可以满足上述边际分布的形式.
但是 \eqref{eq:q_ditui} 式的形式似乎是”一眼法”凑出来的, 不太好理解, 苏剑林在《生成扩散模型漫谈(四):DDIM = 高观点DDPM》给出了一种使用待定系数法求解这个式子形式的方法. 具体来说, 我们有
\[\int q(\xx_{t-1}\vert\xx_t,\xx_0) q(\xx_t\vert\xx_0)d\xx_t = q(\xx_{t-1}\vert\xx_0).\]并且我们要求 \(q(\xx_t\vert\xx_0)=\mathcal{N}(\xx_t;\sqrt{\bar{\alpha}_t}\xx_0,\bar{\beta}_t\bm{I})\), 以及 \(q(\xx_{t-1}\vert\xx_0)=\mathcal{N}(\xx_{t-1};\sqrt{\bar{\alpha}_{t-1}}\xx_0,\bar{\beta}_{t-1}\bm{I})\), 所以我们可以用待定系数法设
\[\label{eq:suppose} q(\xx_{t-1}\vert\xx_t,\xx_0) = \mathcal{N}(\xx_{t-1}; a\xx_t + b\xx_0, \sigma_t^2\bm{I})\]那么我们有
\[\begin{align} \xx_{t-1} &= a\xx_t + b\xx_0 + \sigma_t\bm{\epsilon}_1 \\ &= a\left(\sqrt{\bar{\alpha}_t}\xx_0 + \sqrt{\bar{\beta_t}}\bm{\epsilon}\right) + b\xx_0 + \sigma_t\bm{\epsilon}_1 \\ &= \left(a\sqrt{\bar{\alpha}_t} + b\right)\xx_0 + \sqrt{a^2\bar{\beta_t} + \sigma_t^2}\bm{\epsilon}_2 \end{align}\]最后的式子中没有 \(\xx_t\) 了, 所以在形式上对齐到 \(\xx_{t-1}=\sqrt{\bar{\alpha}_{t-1}}\xx_0 + \sqrt{\bar{\beta}_{t-1}}\bm{\epsilon}_2\), 就有
\[\begin{align} a\sqrt{\bar{\alpha}_t} + b &= \sqrt{\bar{\alpha}_{t-1}} \\ \sqrt{a^2\bar{\beta_t} + \sigma_t^2} &= \sqrt{\bar{\beta}_{t-1}} \end{align}\]结合 \(\bar{\alpha}_t+\bar{\beta}_t=1\), 解得
\[a = \frac{\sqrt{1-\bar{\alpha}_{t-1} -\sigma_t^2}}{\sqrt{1-\bar{\alpha}_t}},\quad b= \sqrt{\bar{\alpha}_{t-1}} - \frac{\sqrt{1-\bar{\alpha}_{t-1} -\sigma_t^2}}{\sqrt{1-\bar{\alpha}_t}}\sqrt{\bar{\alpha}_t}\]代入 \eqref{eq:suppose} 式, 即可得到 \eqref{eq:q_ditui} 式. 注意到实际上 \(\sigma_t\) 也是未知的, 因此我们可以把它看做一个可控制的参数.
我们回头再看 \eqref{eq:q_ditui} 式, 因为我们想要的是 \(q(\xx_{t-1}\vert\xx_t)\) (用于反向过程采样), 而不是 \(q(\xx_{t-1}\vert\xx_t,\xx_0)\), 所以我们需要从式子里去掉 \(\xx_0\). 结合 \(\xx_t = \sqrt{\bar{\alpha}_t}\xx_0 + \sqrt{\bar{\beta_t}}\bm{\epsilon}\), 我们有
\[\xx_0 = \frac{\xx_t-\sqrt{1-\bar{\alpha}_t}\bm{\epsilon}}{\sqrt{\bar{\alpha}_t}}\]上式的 \(\bm{\epsilon}\) 是正向过程采样 \(\xx_t\) 中使用的, 而我们现在是在反向过程中, 需要要反向过程的这一步噪声. 正好, 我们的神经网络就是在拟合反向过程的噪声, 所以我们把上式改写一下
\[\xx_0 = \frac{\xx_t-\sqrt{1-\bar{\alpha}_t}\bm{\epsilon}_{\theta}(\xx_t,t)}{\sqrt{\bar{\alpha}_t}}\]这个时候的 \(\xx_0\) 就是反向过程中用模型一步预测出来的 \(\xx_0\), 那么就可以代入 \eqref{eq:q_ditui} 式加下划线的两个地方, 从而得到
\[\label{eq:sampling} \xx_{t-1} = \sqrt{\bar{\alpha}_{t-1}}\underbrace{\left(\frac{\xx_t-\sqrt{1-\bar{\alpha}_t}\bm{\epsilon}_{\theta}(\xx_t,t)}{\sqrt{\bar{\alpha}_t}}\right)}_{\text{predicted } \xx_0} + \sqrt{1-\bar{\alpha}_{t-1}-\sigma_t^2}\cdot\bm{\epsilon}_{\theta}(\xx_t,t) + \underbrace{\sigma_t\bm{\epsilon}_t}_{\text{random noise}}\]上式就是一个更一般的生成模型的采样方法 (参数化 \(\bm{\epsilon}\)), 取不同的 \(\sigma_t\), 就可以得到不同的生成模型.
我们还可以参数化 \(\xx_0\), 从而得到另一个递推公式:
\[\label{eq:sampling-by-x0} \xx_{t-1} = \sqrt{\bar{\alpha}_{t-1}}\xx_{\theta}(\xx_t,t) + \sqrt{1-\bar{\alpha}_{t-1}-\sigma_t^2}\underbrace{\left(\frac{\xx_t-\sqrt{\bar{\alpha}_t}\xx_{\theta}(\xx_t,t)}{\sqrt{1-\bar{\alpha}_t}}\right)}_{\text{predicted } \bm{\epsilon}} + \underbrace{\sigma_t\bm{\epsilon}_t}_{\text{random noise}}\]其中 \(\xx_{\theta}(\xx_t,t)\) 是通过神经网络 (比如 UNet) 来预测 \(\xx_0\) 的.
DDPM 是一个特例
特别地, 当我们取 \(\sigma_t=\sqrt{\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}} \cdot \sqrt{1-\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}}\) 时, \(\bm{\epsilon}_{\theta}(\xx_t,t)\) 的系数变成了
\[\begin{align} & \sqrt{1-\bar{\alpha}_{t-1}-\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\cdot \left(1-\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}\right)} - \frac{\sqrt{\bar{\alpha}_{t-1}}\sqrt{1-\bar{\alpha}_t}}{\sqrt{\bar{\alpha}_t}} \\ = &\frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{\sqrt{1-\bar{\alpha}_t}} - \frac{\sqrt{\bar{\alpha}_{t-1}}\sqrt{1-\bar{\alpha}_t}}{\sqrt{\bar{\alpha}_t}} \\ = &\frac{\alpha_t(1-\bar{\alpha}_{t-1})}{\sqrt{\alpha_t}\sqrt{1-\bar{\alpha}_t}} - \frac{1-\bar{\alpha}_t}{\sqrt{\alpha_t}\sqrt{1-\bar{\alpha}_t}} \\ = &\frac{\alpha_t-1}{\sqrt{\alpha_t}\sqrt{1-\bar{\alpha}_t}} \\ = &-\frac{\beta_t}{\sqrt{\alpha_t}\sqrt{1-\bar{\alpha}_t}} \\ \end{align}\]这样, 采样方式 \eqref{eq:sampling} 式就变成了
\[\xx_{t-1} = \frac1{\sqrt{\alpha_t}}\left(\xx_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\bm{\epsilon}_{\theta}(\xx_t,t)\right) + \sigma_t\bm{\epsilon}_t,\]这就成了指定 \(\sigma_t=\sqrt{\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}} \cdot \sqrt{1-\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}}\) 的 DDPM 采样过程.
DDIM 也是一个特例
特别地, 当 \(\sigma_t=0\) 时, 采样方式 \eqref{eq:sampling} 式的噪声项就没有了, 这样最终生成的 \(\xx_0\) 的随机性只依赖于初始的 \(\xx_T\). 也就是说, 给定 \(\xx_T\) 后, 生成过程就变成确定性的了, 从而可以看做一个潜变量模型 (作者把它成为隐式模型, implicit model).
采样加速
在上一节我们花了很大的篇幅介绍了在损失函数不变的情况下, 一个特殊的例子: 所有中间状态都依赖 \(\xx_0\) 时采样过程变成了以 \(\sigma_t\) 为参数的一种更灵活的采样方式. 而且当 \(\sigma_t\) 取特殊的序列时, 这个过程可以变成 DDPM 或者 DDIM.
但我们至今还未讨论如何加速 DDPM 的问题, 因为从上一节的推导, 并没有涉及到加速的问题. 但我们已经理解了只要以 \(\xx_0\) 为条件的边际分布的形式不变, 我们就可以任意的定义联合分布, 即前向过程. 那么, 很自然的, 我们可以把原来 \(T=1000\) 步的前向过程变得更短. 下图展示了一个 \(T=3\) 缩短为 \(T=2\) 的过程.

图 4. 加速生成的例子, 其中子序列取 {1, 3}.
也就是说, 我们可以从原始 \(T\) 步扩散中取其中的一个子集 \(\tau\subset\{1,2,\cdots,T\}\) 作为我们的生成过程. 这样, 中间状态 \(\{\xx_{\tau_1},\cdots,\xx_{\tau_S}=\xx_T\}\) 就是一个马尔科夫链, 而被跳过的那些中间状态 \(\{\xx_i\}_{i\in\bar{\tau}}\) 关于 \(\xx_0\) 呈星形, 独立于我们的生成过程, 其中 \(\bar{\tau}=\{1,\cdots,T\}\backslash\tau\).
这样联合分布可以定义为
\[q(\xx_{1:T}\vert\xx_0) = q(\xx_{\tau_S}\vert\xx_0)\prod_{i=1}^S q(\xx_{\tau_{i-1}}\vert\xx_{\tau_i},\xx_0)\prod_{t\in\bar{\tau}}q(\xx_t\vert\xx_0).\]其中 \(q(\xx_{\tau_S}\vert\xx_0)\) 和 \(\prod_{t\in\bar{\tau}}q(\xx_t\vert\xx_0)\) 的每一项我们都直接定义为符合要求的边际分布, 因为给定 \(\xx_0\) 后他们是相互独立的. 而中间的 \(\prod_{i=1}^Sq(\xx_{\tau_{i-1}}\vert\xx_{\tau_i},\xx_0)\) 的每一项我们仍然可以用上一节的定义方式得到和上一节相同的采样公式, 唯一不同的就是这个采样过程 \(S\) 步即可完成.
所以我们想要对一个训练好的 DDPM 模型加速采样的话, 只需指定一组 \(\{\sigma_t\}_{t=1}^S\), 利用采样公式 \eqref{eq:sampling} 即可完成采样. 当我们指定 \(\{\sigma_t=0\}_{t=1}^S\) 的话, 就是加速版的 DDIM 采样, 类似地我们可以获得加速版的 DDPM 采样.
非最优损失函数
再回顾一下 DDPM 的损失函数 (未简化版的):
\[\label{eq:ddpm_loss} L_{\bm{\gamma}} = \sum_{t=1}^T\gamma_t\mathbb{E}_{q(\xx_0),\bm{\epsilon}\sim\mathcal{N}(\bm{0},\bm{I})}\left[\Vert \bm{\epsilon} - \bm{\epsilon}_{\theta}(\sqrt{\bar{\alpha}_t}\xx_0 + \sqrt{1-\bar{\alpha}_t}\bm{\epsilon},t) \Vert^2_2\right]\]其中 \(\gamma_t\) 是一组只和 \(\alpha_t,\beta_t\) 有关的系数. 简化版的 DDPM 损失函数相当于令 \(\bm{\gamma}=\bm{1}\).
DDIM 论文提出保证边际分布不变的前提下, 可以自定义联合分布从而构造更灵活的生成分布. 而构造出来的生成分布对应的损失函数包含一个可变参数 \(\sigma_t\), 按照 DDIM 一节中所有中间状态都依赖于 \(\xx_0\) 的情况, 其损失函数可以类似于 《生成扩散模型(四): 扩散模型和得分匹配》 中 “优化目标” 一小节的推导, 得到如下的损失函数:
\[J_{\bm\sigma} = \mathbb{E}_{q(\xx_{0:T})}\left[q(\xx_T\vert\xx_0)+\sum_{t=2}^T\log{q(\xx_{t-1}\vert\xx_t,\xx_0)}-\sum_{t=1}^T\log{\pt^{(t)}(\xx_{t-1}\vert\xx_t)}-\log{\pt(\xx_T)}\right]\]DDIM 论文中给出了如下定理:
这个定理说明了, 对于任意 \(\bm\sigma\) 的取值, 都可以找到对应的 \(\bm\gamma\) 使得两个目标函数的最优解相同. 这一定程度上说明了 DDIM 论文中使用 DDPM 的预训练模型的合理性.
但是这里需要特别说明, 实际上每一种 \(\bm\sigma\) 的取值都必须对应一种 \(\bm\gamma\) 的特定取值. 但 DDIM 中 \(\bm\sigma\) 的取值实际上并不一定对应 DDPM 中 \(\bm\gamma=\bm{1}\) 的模型.
但是我们知道 DDPM 和 DDIM 都是用的参数共享的 \(\pt^{(t)}=\pt\), 却继续使用 DDPM 训练好的 \(L_{\bm{1}}\) 模型来采样, 所以我们要理解使用 DDIM 的采样方式实际上并不是在 \(J_{\bm\sigma}\) 的最优解上采样的, 因此其采样效果会有一定损失.