Jarvis' Blog (总有美丽的风景让人流连) 总有美丽的风景让人流连

医学影像简介(Medical Imaging Guide)

2019-06-24
Jarvis
Post
图像处理

本文介绍医学影像的一些基础概念, 几种常用的医学图像格式, 以及常用的 Python包(nibabel, SimpleITK)的相关用法. (未完待续)

1. 术语

1.1 切面

  • 冠状面 (Coronal plane): 分离前后
  • 矢状面 (Sagittal plane): 分离左右
  • 横断面 (Transverse plane) / 轴向面(Axial plane): 分离上下

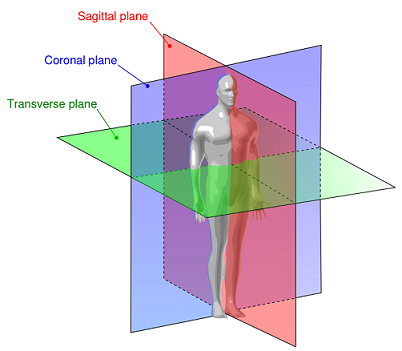
图 1. 医学图像的切面

1.2 方向

以站立的病人自身为参考, 如: 右侧表示病人的右侧, 如下图所示. 病人的右侧通常在屏幕上(医学图像)显示在左侧.

  • 左 (Left)
  • 右 (Right)
  • 前 (Anterior)
  • 后 (Posterior)
  • 上 (Superior)
  • 下 (Inferior)

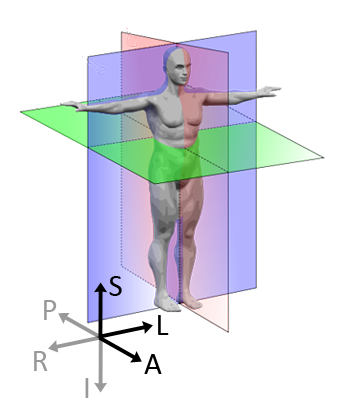
图 2. 医学图像的六个方向

注意1: 使用 up, down, front, back 是不准确的, 因为病人在站立和躺下时这几个概念会混淆, 因此医学中常使用上述的六个(英文)术语来表示上图中的方向.

注意2: 有时候对于对称的结构(如大脑)也会使用中部(Medial) 和侧边(Lateral)来表示方位.

1.3 坐标系统

坐标系统有三种: 世界坐标系, 解剖坐标系和图像坐标系.

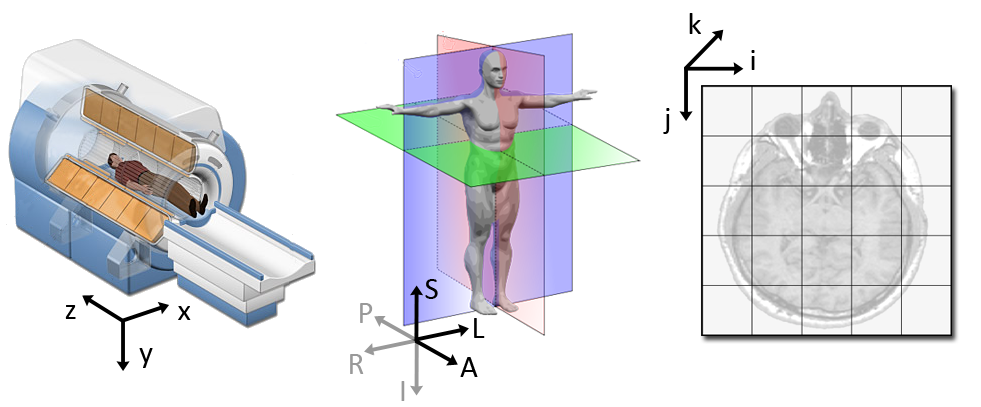
图 3. 医学图像的不同坐标系统

1.3.1 世界坐标系

世界坐标系是笛卡尔坐标系, 每个模型(model, 指病人)都有自己的世界坐标系. 世界坐标系和解剖坐标系的坐标通常都使用 \((x, y, z)\) 来表示, 注意区分.

1.3.2 解剖坐标系(LPS/RAS/RAI)

也称为病人坐标系, 是医学影像技术中最重要的坐标系. 解剖坐标系是一个连续的三维空间, 图像从该空间中采样. 解剖坐标系使用1.2节中的六个方向作为坐标系的正负轴, 接下来需要确定三个轴的正方向. 通常有以下两种:

  • LPS(Left, Posterior, Superior): MHD图像(meta image), ITK工具包, ITK-Snap软件(该软件中写的是RAI, 下文会解释)使用
  • RAS(Right, Anterior, Superior): Nifti图像和3D Slicer软件使用

注意以上两种均为右手坐标系. 其他的选择(如: RPI)和左手坐标系(如: LAS)也是可能遇到的, 需要注意区分.

警告: 人们并不总是用三个连续的字母表示正方向, 有时候也表示出发(from)的方向(也就是负方向), 此时上面的LPS会被写成RAI, 对应的到达(to)方向才是LPS. 比如ITK-Snap软件中Tools->Image Information->Orientation就写的是RAI, 表达的意思是 from RAI --> to LPS , 同样的使用 ITK 导出的MHD格式图像也是使用From模式.

1.3.3 图像坐标系

图像坐标系统描述了图像是如何被采样出来的. 所以图像坐标系统中不仅包含了体素值(三维中的像素一般称为体素 voxel), 还包含采样原点(origin), 采样间距(spacing)等信息.

  • 原点表示图像的第一个体素在解剖坐标系中的坐标, 如(100mm, 50mm, -25mm)
  • 间距表示沿着每个轴相邻体素之间的距离, 如 (1.5mm, 0.5mm, 0.5mm)

下图是一个二维图像原点和间距的示意图.

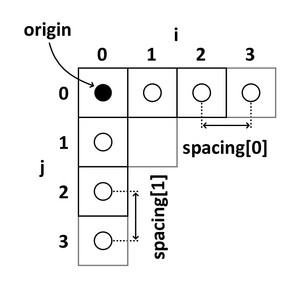
图 4. 图像像素原点和间距示意图

通过原点和间距我们就可以计算图像中任意一个体素在解剖坐标系的坐标.

1.3.4 图像变换

从图像空间坐标 \((i,j,k)^T\) 变换到解剖空间的坐标 \((x, y, z)^T\) 需要用一个仿射变换, 包含了一个线性变换矩阵 \(\mathbf{A}\) 和一个平移向量 \(\mathbf{t}\) :

\[\left[\begin{matrix}x_1\\x_2\\x_3\end{matrix}\right]=\left[\begin{matrix}A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}\end{matrix}\right]\left[\begin{matrix}i\\j\\k\end{matrix}\right]+\left[\begin{matrix}t_1\\t_2\\t_3\end{matrix}\right].\]

为了方便我们可以把上式合并为一个矩阵向量乘法:

\[\left[\begin{matrix}x_1\\x_2\\x_3\\1\end{matrix}\right]=\left[\begin{matrix}A_{11}&A_{12}&A_{13}&t_1\\A_{21}&A_{22}&A_{23}&t_2\\A_{31}&A_{32}&A_{33}&t_3\\0&0&0&1\end{matrix}\right]\left[\begin{matrix}i\\j\\k\\1\end{matrix}\right].\]

而上面的 \(4\times4\) 矩阵也根据解剖空间的方向(LPS或RAS)称为 IJKtoLPS- 或 IJKtoRAS-矩阵.

1.3.5 例子

下面给一个二维的例子.

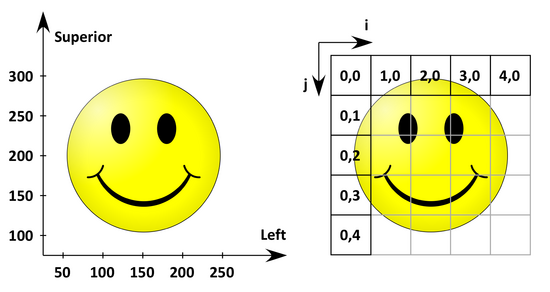
图 5. 图像坐标系转解剖坐标系LS

上图中可以看到沿着 \(i\) 增大的方向 Left 轴是增加的, 沿着 \(j\) 增大的方向 Superior 轴是减小的, 因此变换矩阵的对角线上第一行(对应 \(i\)) 是正的, 第二行(对应 \(j\)) 是负的. 没有旋转, 所以变换矩阵只有对角线非零. 两个方向的像素间距均为 \(50\). 像素 \((0, 0)\) 的解剖坐标为 \((50, 300)\), 所以我们最后得到变换矩阵为

\[\nonumber IJtoLS = \left[\begin{matrix}50&0&50\\0&-50&300\\0&0&1\end{matrix}\right].\]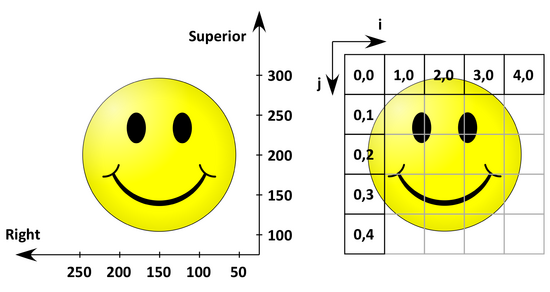

图 6. 图像坐标系转解剖坐标系RS

类似地我们可以得到左手坐标系的变换矩阵

\[\nonumber IJtoLS = \left[\begin{matrix}-50&0&250\\0&-50&300\\0&0&1\end{matrix}\right].\]

有时候我们拿到的图像数据已经包含了变换矩阵, 因此我们可以根据变换矩阵知道使用了哪种坐标系. 需要注意的是我们这里指的图像坐标系是未经过软件变换的. 在具体使用任何软件浏览医学图像时都应当检查坐标原点的位置(可能是左上或左下)后再按照上面的规则进行任何后续的判断.

2. Nifti 格式 (*.nii, *.nii.gz)

Nifti 格式使用 RAS (Right, Anterior, Superior) 作为坐标系的正方向.

2.1 图像读取

使用 SimpleITK 读取

1
2
3

import SimpleITK as sitk
itk_image = sitk.ReadImage("file_path.nii")
arr_image = sitk.GetArrayFromImage(itk_image)

使用 nibabel 读取

1
2
3
4

import nibabel as nib
nib_image = nib.load("file_path.nii")
header = nib_image.header
arr_image = nib_image.get_data()

2.2 元信息 (meta information)

2.2.1 四元组 (quaternion)

在 Nifti 格式的数据中使用四元组表示旋转矩阵. 从元信息中获取四元组:

1
2
3
4

import nibabel as nib
nib_image = nib.load("file_path.nii")
header = nib_image.header
quaternion = header.get_qform_quaternion()

四元组表示为 \((w, x, y, z)\), 满足 \(w^2+x^2+y^2+z^2=1\). 那么四元组转化成旋转矩阵的公式为

\[\mathbf{R}=\left[\begin{matrix}w^2+x^2-y^2-z^2&2(xy-wz)&2(xz+wy)\\2(xy+wz)&w^2+y^2-x^2-z^2&2(yz-wx)\\2(xz-wy)&2(yz+wx)&w^2+z^2-x^2-y^2\end{matrix}\right]\]

对于未归一化的四元组, 需要归一化后计算旋转矩阵, 公式如下

\[\begin{align}\nonumber &N = w^2+x^2+y^2+z^2 \\\nonumber &s=\begin{cases}0&\text{if}~N=0\\ 2/N&\text{otherwise}\end{cases} \\\nonumber \\\nonumber &wx=s\times w\times x\quad wy=s\times w\times y\quad wz=s\times w\times z \\\nonumber &xx=s\times x\times x\quad xy=s\times x\times y\quad xz=s\times x\times z \\\nonumber &yy=s\times y\times y\quad yz=s\times y\times z\quad zz=s\times z\times z \\\nonumber \\ &\mathbf{R}=\left[\begin{matrix}1-yy-zz&xy-wz&xz+wy\\xy+wz&1-xx-zz&yz-wx\\xz-wy&yz+wx&1-xx-yy\end{matrix}\right] \end{align}\]

2.2.2 qform 仿射矩阵

  • 像素间距 header['pixdim'][1:4] , 恒为正数
  • 符号因子 header['pixdim'][0], 取值于 {-1, 1} , 其他值均视为1.
  • 原点(即偏移) header['qoffset_x'], header['qoffset_y'], header['qoffset_z']

仿射矩阵 qform 的构造如下

\[\mathbf{Q} = \left[\begin{matrix}\mathbf{RS}&\mathbf{t}\\\mathbf{0}&1\end{matrix}\right]\]

其中 \(\mathbf{t}=(t_1, t_2, t_3)^T\) 为原点(偏移), \(\mathbf{S}\) 为像素间距 \((s_1~s_2~s_3)\) 拓展的对角阵

\[\mathbf{S}=\left[\begin{matrix}s_1&0&0\\0&s_2&0\\0&0&qs_3\end{matrix}\right]\]

其中 \(q\) 为 qfac 值, 为符号因子.

2.2.3 sform 仿射矩阵

前三行取自 header['srow_x'], header['srow_y'], header['srow_z'] , 最后一行填值 (0 0 0 1) .

2.2.4 qform_code 和 sform_code

qform 和 sform 的存在是为了更灵活的从图像坐标系到解剖坐标系的变换. Nifti 使用 qform_code 和 sform_code 来表示选择哪种方式变换. 如下表

Name Code Description
Unknown 0 任意坐标, 使用方法1
Scanner_ANAT 1 Scanner-based anatomical coordinates.
Aligned_ANAT 2 Coordinates aligned to another file, or to the “truth” (with an arbitrary coordinate center).
Talairach 3 对齐到 Talairach 空间的坐标 (人脑的三维坐标系, 即图谱).
Mni_152 4 对齐到 mni 空间的坐标 (另一个人脑三维坐标系).

其中 qform_code 应该包含于 (0 1 2) (对应于下面的方法2), 而 sform_code 可以是以上任意一个 Code.

方法1: 转换仅使用像素间隔

\[\left[\begin{matrix}x_1\\x_2\\x_3\end{matrix}\right]=\left[\begin{matrix}i\\j\\k\end{matrix}\right]\odot\left[\begin{matrix}\text{pixdim[1]}\\\text{pixdim[2]}\\\text{pixdim[3]}\end{matrix}\right].\]

其中 \(\odot\) 表示点乘.

方法2: 当 qform_code > 0 时使用该方法

\[\left[\begin{matrix}x_1\\x_2\\x_3\end{matrix}\right]=\mathbf{R}\left[\begin{matrix}i\\j\\qk\end{matrix}\right]\odot\left[\begin{matrix}\text{pixdim[1]}\\\text{pixdim[2]}\\\text{pixdim[3]}\end{matrix}\right]+\left[\begin{matrix}\text{qoffset_x}\\\text{qoffset_y}\\\text{qoffset_z}\end{matrix}\right].\]

方法3: 当 sform_code > 0 时使用该方法

\[\left[\begin{matrix}x\\y\\z\\1\end{matrix}\right]=\left[\begin{matrix}\text{srow_x[0]}&\text{srow_x[1]}&\text{srow_x[2]}&\text{srow_x[3]}\\\text{srow_y[0]}&\text{srow_y[1]}&\text{srow_y[2]}&\text{srow_y[3]}\\\text{srow_z[0]}&\text{srow_z[1]}&\text{srow_z[2]}&\text{srow_z[3]}\\0&0&0&1\end{matrix}\right]\left[\begin{matrix}i\\j\\k\\1\end{matrix}\right].\]

2.3 使用和查看图像

2.3.1 使用 nibabel 读取

这里主要指使用第三方库 (如 matplotlib) 使用和查看图像. 由于通常来说第三方库在显示图像时会把左上角的像素坐标设为 \((0, 0)\) , 因此我们通常也希望使用和查看 Nifti 图像时也能够在左上角像素为 \((0, 0)\) 时图像是摆正的.

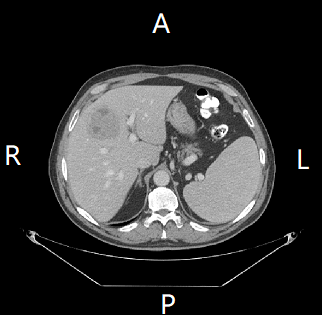
图 7. 肝脏图像

比如我们从 Nifti 格式的数据中读取一个肝脏的CT图像, 由于 Nifti 格式使用的是 RAS 坐标系(即上图中R轴向左, A轴向上), 而图像坐标系相反(i轴向右, j轴向下), 所以只需要让变换矩阵中位置 \((0, 0)\) 的元素和位置 \((1, 1)\) 的元素均为负数即可.

在一般的 Nifti 图像中, sform 和 qform 可能同时存在, 此时使用 header.get_best_affine() 的读取顺序为

  • sform_code 不为0时(0表示unknown), 使用 sform , 否则
  • qform_code 不为0时, 使用 qform, 否则
  • 使用默认的仿射矩阵 header.get_base_affine() , 详细信息参考 nibabel 相关函数的源码

假设我们使用函数 header.get_best_affine() 从该文件中读取到的变换矩阵 affine 为

\[\left[\begin{matrix}-0.97656202&0.&0.&249.1000061\\0.&0.97656202&0.&-249.0231781\\0.&0.&2.5&-651\\0.&0.&0.&1.\end{matrix}\right]\]

那么我们发现位置 \(\text{affine}(0, 0)=-0.97656202<0\), 符合要求, 而 \(\text{affine}(1, 1)=0.97656202>0\), 不符合要求, 所以需要对 j 轴(即 height) 做一个反转即可, 可以用如下的代码

1
2
3
4
5
6
7
8
9
10

import nibabel as nib
nib_image = nib.load("file_path.nii")
affine = nib_image.header.get_best_affine()
arr_image = nib_image.get_data()

# arr_image: [depth, height, width]
if affine[0, 0] > 0:
	arr_image = numpy.flip(arr_image, axis=0)
if affine[1, 1] > 0:
	arr_image = numpy.flip(arr_image, axis=1)

2.3.2 使用 nibabel 保存

使用 nibabel 保存时如果有参照图像的话最好直接使用参照图象的 header 进行保存 (如: label可以使用图像的header). 如果没有可以参照的header时, 就需要自己给定仿射矩阵或者header. 保存的命令如下

1
2
3
4

# 输入 Nifti1Image 的三维数组的轴应该是 (x, y, z) 的顺序, 而一般之前输出的为 (z, y, x) 的顺序, 所以需要转置一下.
out_image = np.transpose(arr_image, (2, 1, 0))
out = nib.Nifti1Image(out_image, affine=affine, header=header)
nib.save(out, out_path)

这里的 affine 参数和 header 参数一般只填一个比较好. 如果有参照图像则直接使用参照图像的 header , 没有的话使用 affine 参数. 这里的 affine 会填充到 sform 中, 因此是一个 \(4\times4\) 的矩阵. 同样地我们为了符合 Nifti 的 RAS 坐标体系, 填充以下矩阵可以保证图像是正的

\[\left[\begin{matrix}-1&0&0&0\\0&-1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right].\]

所以如果想要使用 affine=np.eye(4) 的话, 为了把图像摆正, 就需要在输出前对图像沿x轴和y轴做翻转(显然这样有点多此一举, 因此下次读进来想正着用的话又得做两次翻转).

2.3.2 使用 SimpleITK

使用 SimpleITK 时我们无法直接获取 qform 矩阵, 但可以获得所有的元信息. 所以需要按照 2.2 节的讨论使用元信息进行计算, 但是实际上 SimpleITK 已经帮我们计算好并转化成了 ITK 格式的方向矩阵.

1
2
3
4
5
6
7
8

import SimpleITK as sitk
itk_image = sitk.ReadImage("file_path.nii")
arr_image = sitk.GetArrayFromImage(itk_image)
direction = itk_image.GetDirection()	# [1, 0, 0, 0, -1, 0, 0, 0, 1] reshape成3x3矩阵即可
if direction[0] < 0:
    arr_image = numpy.flip(arr_image, axis=0)
if direction[4] < 0:
    arr_image = numpy.flip(arr_image, axis=1)

注意到我们上面的讨论都没有考虑 z 方向. 这里是为了讨论的方便, z 方向的规则基本相同, 只需要额外注意乘上 Nifti 中的符号因子 qfac 即可.

3. Meta 格式 (*.mhd+*.raw)

3.1 标签 (tags)

1
2
3
4
5
6
7
8
9
10
11
12
13

ObjectType = Image
NDims = 3
BinaryData = True
BinaryDataByteOrderMSB = False
CompressedData = False
TransformMatrix = 1 0 0 0 0 -1 0 1 0
Offset = -253.125 -95 250
CenterOfRotation = 0 0 0
AnatomicalOrientation = RSA
ElementSpacing = 1.5625 1.5625 10
DimSize = 322 1078 20
ElementType = MET_SHORT
ElementDataFile = Series28.raw

说明:

  • BinaryDataByteOrderMSB 中的 MSB 表示 big-endian
  • TransformMatrix 为 \(3\times3\) 的矩阵, 按列存储, 上面的一行转换为矩阵是
\[\left[\begin{matrix}1&0&0\\0&0&1\\0&-1&0\end{matrix}\right]\]
  • Offset 为图像的第一个像素在解剖坐标系中的坐标
  • CenterOfRotation 旋转中心
  • AnatomicalOrientation 为解剖坐标系的From方向(关于From方向和正方向的解释参考1.3.2节). 这里做一个详细的解释:
    • 该参数实际上是直接从TransformMatrix中算出来的. Meta Image默认的From方向为RAI, 与ITK相同.
    • 上例中变换矩阵第三行的非零值为负数, 所以RAI的第三轴变方向, 变为RAS
    • 变换矩阵第二三行交换了顺序(相对于单位阵), 所以RAS的第二三轴换序, 变为RSA
  • DimSize 为图像的尺寸
  • ElementType 为数据格式, 这里是 short , 即 16位有符号整数
  • ElementDataFile 为数据路径
  • 数据存储在 *.raw 文件中, 纯数据文件, 数据的读取的方式根据 DimSize 和 ElementType 决定.

4. DICOM 格式 (*.dcm)

未完待续…

Reference

第1节

  • http://www.grahamwideman.com/gw/brain/orientation/orientterms.htm
  • https://www.slicer.org/wiki/Coordinate_systems

第2节

  • https://brainder.org/2012/09/23/the-nifti-file-format/
  • https://nipy.org/nibabel/nifti_images.html

第3节

  • https://itk.org/Wiki/ITK/MetaIO/Documentation
  • http://www.itksnap.org/pmwiki/pmwiki.php

上一篇 Latex 符号

下一篇 机器学习中的优化器(Optimizers in Machine Learning)

Content