支持向量机 (Suppoert Vector Machine)

• 1. 线性可分 SVM 问题构建
  • 1.1 几何间距
  • 1.2 硬间隔最大化
  • 1.3 问题的求解
  • 1.4 求解对偶问题
  • 1.5 构造分类器
  • 1.6 支持向量
• 2. 线性不可分 SVM 与软间隔最大化
  • 2.1 软间隔最大化
  • 2.2 求解对偶问题
  • 2.3 构造分类器
  • 2.4 支持向量
  • 2.5 合页损失函数 (hinge loss)
• 3. SVM 的核方法
  • 3.1 核函数
  • 3.2 C - 支持向量分类机
• 4. Appendix*
• 5. Reference

支持向量机 (support vector machine, SVM) 是一类有监督地对二元数据分类的广义线性分类器, 其决策边界是对学习样本求解的最大间隔超平面.

问题来源: 超平面 (hyperplane) 分类器的不唯一性.

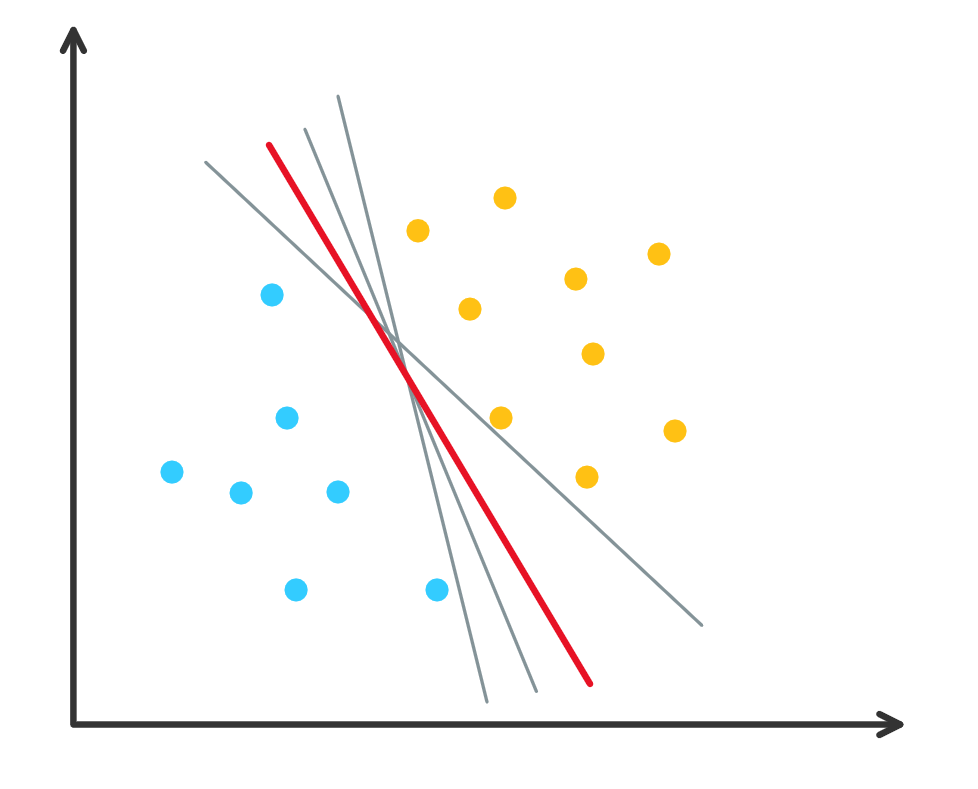
图 1. 超平面分类器的不唯一性

因此需要给定一个准则来选择一个最优的超平面.

$$ \def\xx{\mathbf{x}} \def\ww{\mathbf{w}} \def\vw{\lVert\ww\rVert} \def\sui{\sum_{i=1}^n} \def\suj{\sum_{j=1}^n} $$

1. 线性可分 SVM 问题构建

线性 SVM 的意思是使用一次函数作为 SVM 分类器, 可分的意思是当前的数据是可以使用分类器完全划分开的, 即可以使用一条直线(二维情况)把数据的两个类别完全分隔开¹.

1.1 几何间距

令 \(\gamma\) 表示空间一点 \(\xx\) 到超平面

的距离, \(\ww\) 为超平面的法向. 设 \(\xx\) 正投影到超平面的点为 \(\xx_0\) , 则有

其中 \(y\) 取值为 \(1\) 或 \(-1\), 表示 \(\xx\) 在超平面的上方/下方. 如下图所示.

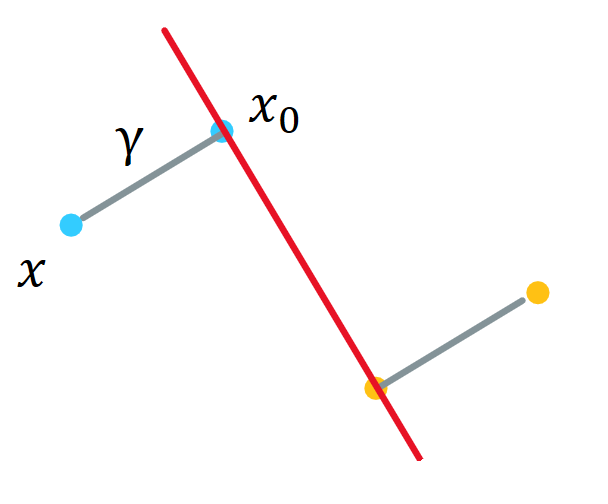
图 2. 几何距离

1.2 硬间隔最大化

因为 \(\xx_0\) 落在超平面上, 所以代入公式 \(\eqref{eq:hyperplane}\) 得到

解得

当超平面在小范围内改变时, 超平面附近点的分类可能会发生变化, 而离超平面远的点的分类不会发生变化. 因此我们要寻找一个尽可能在两类点”中间”的一个超平面(即既要把两类点分开, 还要离两类点尽可能的远), 如下图中红色的线. 这种准则称为最大化间隔 (maximum margin).

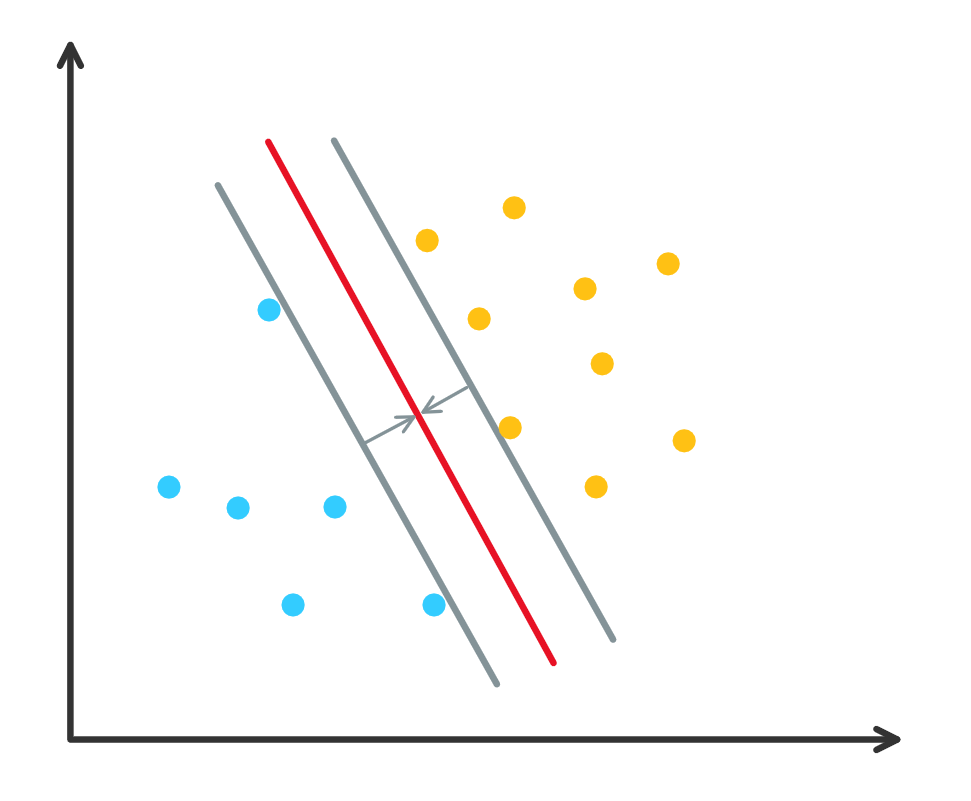
图 3. 最大化间隔

注: 这里是硬间隔最大化, 因为数据点是线性可分的, 因此强制要求该超平面距离两类点尽可能地远..

由此我们可以得到一个最大化间隔的分类器:

其中 \(\gamma_i\) 表示训练集中第 \(i\) 个点到超平面的距离. 由于分子项 \(y(\ww^T\xx + b)\) 可以在不改变超平面的前提下任意变大, 因此为了方便我们固定 \(\gamma\vw=y(\ww^T\xx + b)=1\) . 从而这个问题就变为了

即

注: 对于直线 \(y=ax+3\) , 其对应的 \(\ww=(a, -1)^T, b=3\) . 我们同时把 \(\ww\) 和 \(b\) 乘以同样的系数 \(2\), 则 \(\ww=(2a, -2)^T, b=6\) 直线方程变为 \(2y=2ax+6\) 和原来的方程等价. 因此在表示同一个超平面的情况下 \(\ww\) 和 \(b\) 可以成比例的缩放.

最后我们的分类器可以表示为:

其中目标函数增加 \(1/2\) 和平方是为了优化的方便, 其最小值不会因此而改变. 注意到公式 \(\eqref{eq:classifier}\) 中的不等式约束, 离目标超平面远的点的约束其实是不必要的, 因为他们会被离超平面更近点的约束所包含, 因此实际起作用的约束所对应的点是我们关心的, 这些点称为支持向量 (support vector), 如下图所示, 蓝色圈中的点为支持向量, 这三个点对应的不等式约束是实际起作用的.

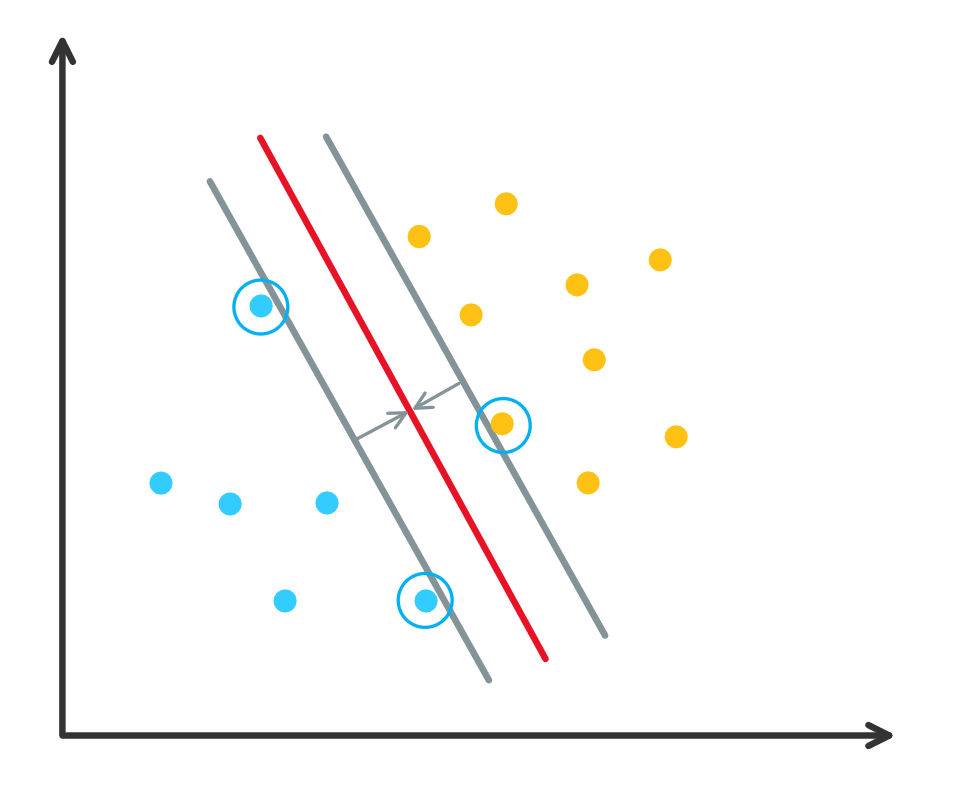
图 4. 支持向量

1.3 问题的求解

直接求解原问题是一个带不等式约束的凸二次规划问题(convex quadratic programming), 可以使用凸优化算法求解.

• Python 上的凸优化包 CVXOPT

1.4 求解对偶问题

带不等式约束的优化问题可以转为对偶问题求解. 使用 Lagrange 乘子法, 优化问题 \(\eqref{eq:classifier}\) 可以变为

其中 \(\boldsymbol\alpha=(\alpha_1,\cdots,\alpha_n)^T\) 为 Lagrange 乘子向量.

定理: 最优化问题 \(\begin{align}\nonumber \max_{\alpha} &\quad-\frac12\sui\suj y_iy_j\cdot\xx_i^T\xx_j\cdot\alpha_i\alpha_j+\suj\alpha_j, \\ \text{s.t.} &\quad\sui y_i\alpha_i=0,\\ \nonumber &\quad\alpha_i\geq0,\;i=1,\cdots, n \end{align}\)

是原始问题 \(\eqref{eq:classifier}\) 的对偶问题. 这里可以用极小化代替目标函数的负数的极大化.

把原问题转化为对偶问题求解有两个好处:

• 对偶问题一般来说更容易求解
• 在对偶问题中仅包含了关于数据点 \(i, j\) 的内积 \(\xx_i^T\xx_j\) 的形式, 从而通过引入核方法(kernel method) 可以把 SVM 泛化为更加复杂的分类器.

1.5 构造分类器

最后可以根据对偶问题的解 \(\boldsymbol\alpha^*\) 计算原始问题的解:

选择 \(\boldsymbol\alpha^*\) 的一个满足 \(\alpha_i^*>0\) 的分量计算 (注意这里要选择严格正的分量):

得到分类器:

1.6 支持向量

根据对偶问题的解 \(\boldsymbol\alpha^*\) , 我们把分量 \(\alpha_i^*\) 对应的样本点 \(\xx_i\) 称为支持向量. 根据 KKT 互补条件 可知

那么对于 \(\alpha_i^*>0\) 的样本点, 必然有 \(y_i(\ww^T\xx_i+b)=1\), 从而得到 \(\ww^T\xx_i+b=\pm1\) , 那么点 \(\xx_i\) 一定在间隔边界上. 这与我们在前面给出的支持向量的定义是吻合的.

2. 线性不可分 SVM 与软间隔最大化

2.1 软间隔最大化

线性可分 SVM 对于线性不可分的数据是不适用的, 因为上述不等式约束对于部分数据点无法满足. 此时需要修改原来的不等式约束(硬间隔最大化)为软间隔最大化².

原来硬间隔最大化可以满足 \(y_i\ww^T\xx_i+b\geq1\) , 线性不可分问题的数据点不一定可以满足该公式, 因此引入松弛变量 \(\xi_i>0\) 加到函数间隔上即可使其满足:

对于每个松弛变量我们发现取到正无穷大也会满足约束, 但这样就相当于没有了约束, 因此我们同时要求松弛变量尽可能小, 需要在代价函数增加一项作为惩罚:

其中 \(C>0\) 为超参数, \(C\) 越大, 对误分类的数据点惩罚越大.

那么线性不可分 SVM 的目标函数变为如下的凸二次规划

注意, 这里的问题关于 \((\ww, b, \xi)\) 的解是存在的, 其中 \(\ww\) 的解唯一, 但 \(b\) 的解可能不唯一, 而是存在于一个区间.

2.2 求解对偶问题

使用 Language 乘子法, 带松弛变量的优化问题 \(\eqref{eq:cla2}\) 可以变为

其中 \(\boldsymbol\alpha=(\alpha_1,\cdots,\alpha_n)^T,~\boldsymbol\beta=(\beta_1,\cdots,\beta_n)^T\) 均为 Lagrange 乘子向量.

定理: 最优化问题 \(\begin{align} \nonumber \max_{\alpha}\quad &-\frac12\sui\suj y_iy_j\cdot\xx_i^T\xx_j\cdot\alpha_i\alpha_j+\suj\alpha_j, \\ \nonumber \text{s.t.}\quad &\sui y_i\alpha_i=0,\\ \nonumber &C - \alpha_i - \beta_i = 0,~i = 1,\cdots, n, \\ \nonumber &\alpha_i\geq0,\;i=1,\cdots, n, \\ \nonumber &\beta_i\geq0,\;i=1,\cdots, n \\ \end{align}\)

是原始问题 \(\eqref{eq:cla2}\) 的对偶问题.

上面的定理可以消去 \(\boldsymbol\beta\) 而简化为

2.3 构造分类器

线性不可分 SVM 最终构造分类器的公式与可分 SVM 的相同, 求出 \(\ww^\*\) 和 \(b^\*\) 即可, 计算 \(b^\*\) 的时候选择的 \(\boldsymbol\alpha^\*\) 的分量应当满足 \(0<\alpha_i^*<C\) , 类似的这里不能取等号.

2.4 支持向量

在线性不可分的情况下, 把对偶问题 \(\eqref{eq:cla2_dual}\) 的解 \(\boldsymbol\alpha^\*=(\alpha_1^\*,\alpha_2^\*,\cdots,\alpha_n^\*)^T\) 中对应于 \(\alpha_i^*>0\) 的数据点 \(\xx_i\) 称为(软间隔的)支持向量. 如下图所示.

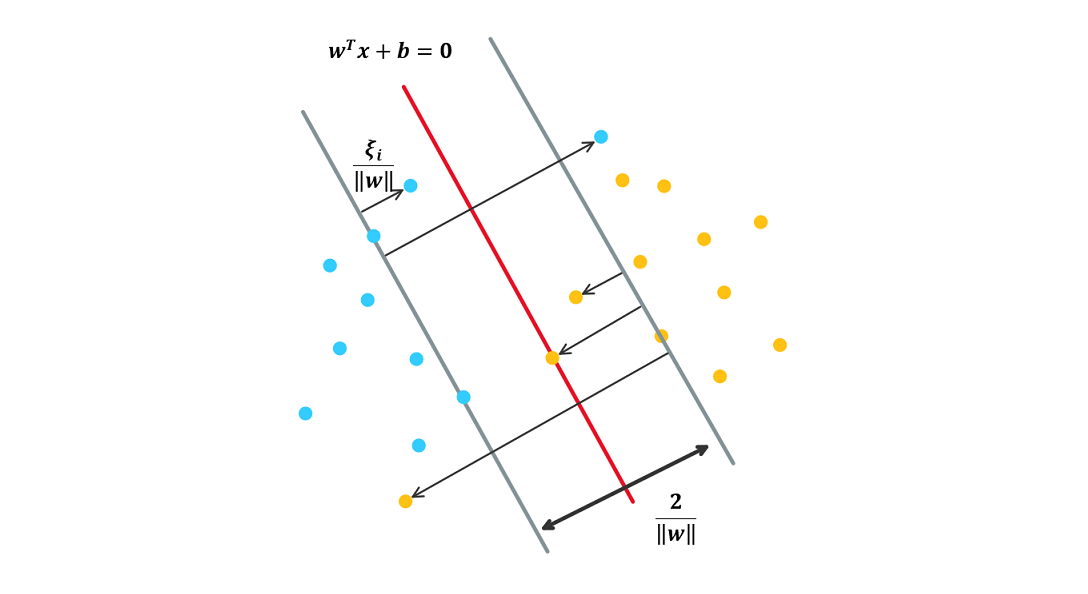
图 5. 软间隔支持向量机分类超平面, 存在误分的数据点

软间隔的支持向量可能落在 (1) 间隔边界上 (2) 间隔边界到分离超平面之间 (3) 分离超平面误分的一侧:

• 若 \(\alpha_i^*=0\), 则 \(\xi_i=0\), 数据点为间隔边界两侧的点
• 若 \(0<\alpha_i^* < C\) , 则 \(\xi_i=0\), 数据点落在间隔边界上, 是支持向量
• 若 \(\alpha_i^*=C\) 且 \(0<\xi_i<1\) , 则数据点落在间隔边界到分离超平面之间
• 若 \(\alpha_i^*=C\) 且 \(\xi_i=1\) , 则数据点落在分离超平面上
• 若 \(\alpha_i^*=C\) 且 \(\xi_i>1\) , 则数据点落在分离超平面误分的一侧

后三条结论可以根据公式 \(\eqref{eq:soft}\) 得出.

2.5 合页损失函数 (hinge loss)

线性 SVM 由以下几部分组成:

1. 模型: 分离超平面 \(\ww^{\*T}\xx+b^*=0\)
2. 决策函数: \(f(\xx)=\text{sign}(\ww^{\*T}\xx+b^*)\)
3. 学习策略: 软间隔最大化
4. 求解算法: 凸二次规划

根据最初对线性 SVM 的期望, 其损失函数也可以按如下方式构造:

其中第一项为经验损失, \(L[x]=[1-x]_+=\text{Relu}(1-x)\) 称为合页损失函数(hinge loss), 当样本点的分类 \(y_i(\ww^T\xx_i+b)>1\) 时, 损失为0, 反之损失线性递增. 目标函数的第二项为正则化项. 可以证明优化问题 \(\eqref{eq:hinge}\) 与优化问题 \(\eqref{eq:cla2}\) 等价. 合页损失函数的图像如下图所示.

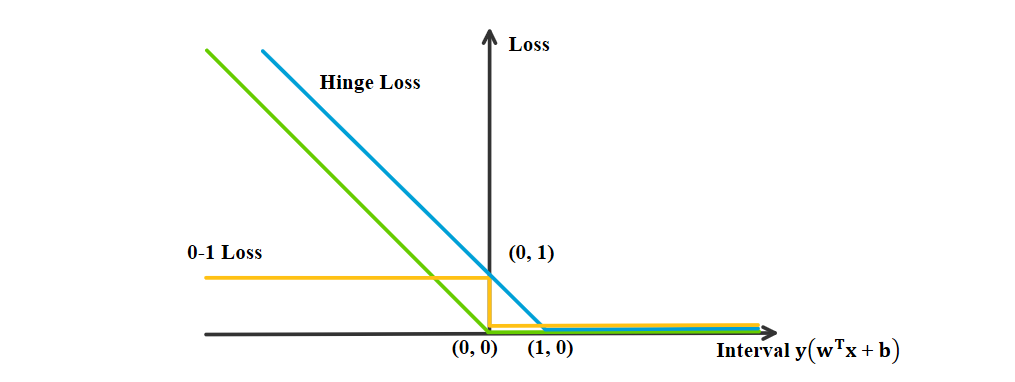
图 6. 合页损失函数与感知机损失, 0-1损失对比

3. SVM 的核方法

核方法可以把普通的线性 SVM 推广到非线性. 核方法的直观来自于数据点升维. 如下图中二维的点.

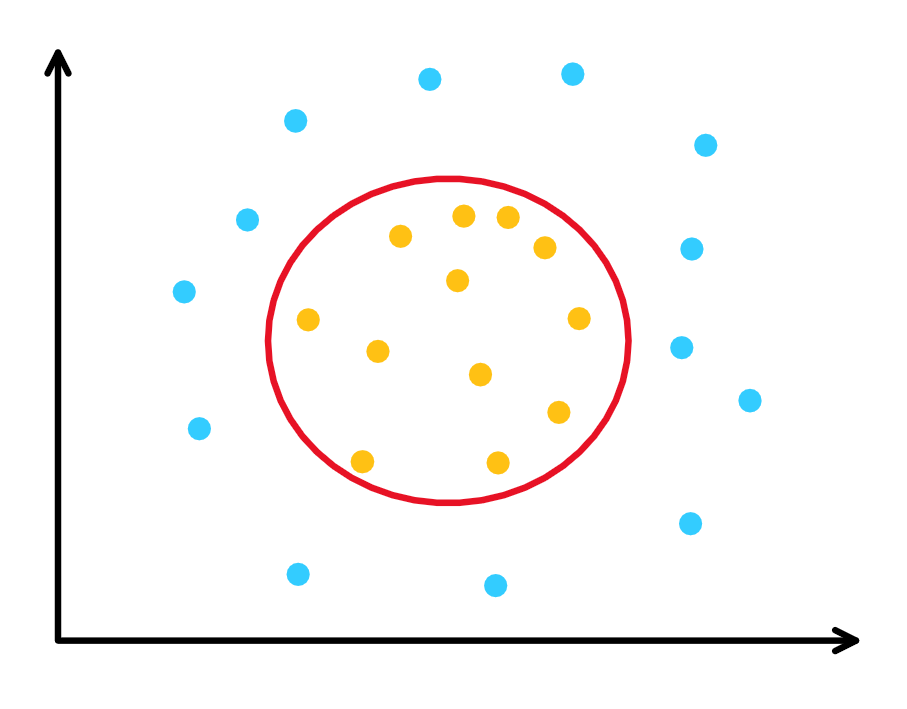
图 7. 非线性分类器

线性分类器无法得到圆形的分类边界, 但是如果通过某个函数 \(\Phi(\cdot)\) 把点映射到三维空间(比如映射成锥形, 中间点的值较小, 周围点的值较大), 那么就可以找到一个三维空间中的二维平面把两类点分开. 如此我们只需要把第1节和第2节中所有的 \(\xx\) 替换为 \(\Phi(\xx)\) , 其他保持不变即可得到非线性 SVM 对应的推导.

3.1 核函数

可以发现在求解对偶问题时, \(\Phi(\xx_i)\cdot\Phi(\xx_j)\) 总是以内积的形式出现, 因此我们可以把这样的形式定义为一个关于 \(\xx_i\) 和 \(\xx_j\) 的二元函数 \(K(\cdot,\cdot)\)

这样我们仍然可以得到相同的决策函数而简化了计算方式以及 \(\Phi(\cdot)\) 函数的构造.

核函数的种类 \(\def\kk{K(x_1,x_2)}\):

• \(\kk = (x_1\cdot x_2)\) 是核函数
• \(f(\cdot)\) 是定义在 \(R^n\) 上的实值函数, 则 \(\kk = f(x_1)f(x_2)\) 是核函数
• 核函数的和与积都是核函数
• 若 \(K_1(x_1, x_2)\) 是 \(R^m\times R^m\) 上的核函数, \(\theta(x)\) 是从 \(R^n\) 到 \(R^m\) 上的映射, 则 \(K_2(x_1, x_2) = K_1(\theta(x_1), \theta(x_2))\) 是 \(R^n\) 到 \(R^n\) 上的核函数. 特别的, 若矩阵 \(B\) 半正定, 则 \(\kk = x_1^TBx_2\) 是 \(R^n\) 到 \(R^n\) 上的核函数.

常用的核函数:

• 多项式核函数 \(\kk = (x_1\cdot x_2)^d\) 和 \(\kk = (x_1\cdot x_2 + 1)^d\)
• Gauss 径向基函数 \(\kk = \exp\left(\frac{-\lVert x_1-x_2\rVert^2}{\sigma^2}\right)\)

3.2 C - 支持向量分类机

使用步骤:

1. 选择核函数 \(K(\cdot,\cdot)\) 和惩罚参数 \(C\geq0\)

2. 求解优化问题:

   \[\begin{align} \min_{\alpha}\quad &\frac12 \sui \suj y_iy_j\cdot K(\xx_i,\xx_j)\cdot\alpha_i\alpha_j- \suj \alpha_j, \\ \text{s.t.}\quad & \sui y_i\alpha_i=0, \\ &0\leq\alpha_i\leq C,~i=1,\cdots,n, \end{align}\]

   的解为 \(\boldsymbol\alpha^\*=(\alpha_1^\*,\cdots,\alpha^\*_n)\) .

3. 计算 \(b^\*\) , 选择位于区间 \((0, C)\) 的 \(\alpha^\*\) 的分量 \(\alpha^\*_j\) , 据此计算

   \[b^* = y_j - \sui y_i\alpha_i^*K(\xx_i, \xx_j);\]

4. 构造决策函数

   \[f(\xx) = sign(\sui y_i\alpha_i^\*K(\xx_i, \xx) + b^*).\]

5. 获得支持向量* : 支持向量为 \(\{(\xx_j, y_j)\lvert \alpha^*_j=0\}\) .

4. Appendix*

• SVM 函数库: LibSVM

5. Reference