Graph Cuts for Segmentation

1. Introduction
2. Graph Cuts and Computer Vision
3. Segmentation Technique
- 3.1 Details
- 3.2 Min-Cut
4. Examples
5. Appendix*
6. References

Title: Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Object in N-D Images

Author: Yuri Y. Boykov, Marie-Pierre Jolly

本文是基于 Graph-Cuts 进行自然图像/医学图像分割的一篇奠基之作, 许多常用的图割方法(如 GrabCut)是基于本文而设计的. 本文的两名作者均来自于西门子公司研究中心.

1. Introduction

图割法是计算机视觉领域分割任务常用的方法. 本文提出了交互式图割法, 同时结合软约束(soft constraint)和硬约束(hard constraint)明确地定义损失函数, 并得到全局最优解.

考虑任意一个点的集合 $\mathcal{P}$ 和点对的集合

\[\mathcal{N}:=\{(p,q)\lvert (p,q)=(q,p),\; p, q\in\mathcal{P}\}.\]

令 $A=(A_1, \cdots, A_p, \cdots, A_{\lvert\mathcal{P}\rvert})$ 表示二值向量, 元素 $A_p$ 代表集合 $\mathcal{P}$ 中像素 $p$ 的一种赋值(0或1, 前景或背景), 从而 $A$ 即表示一种分割. 那么我们加在分割 $A$ 的边界和区域上的软约束可以表示为损失函数 $E(A)$ :

\[E(A) := \lambda R(A) + B(A),\]

其中

\[\begin{align} R(A) &:= \sum_{p\in\mathcal{P}}R_p(A_p) \\ B(A) &:= \sum_{(p,q)\in\mathcal{N}}B_{(p,q)}\cdot\delta(A_p\cdot A_q), \end{align}\]

且

\[\delta(A_p, A_q)= \begin{cases} 1 & \text{if } A_p\neq A_q \\ 0 & \text{otherwise}. \end{cases}\]

区域项 $R(A)$ 表示给像素 $p$ 赋以”前景”或”背景”的惩罚, 边界项 $B(A)$ 中 $B_{(p, q)}\geq0$ 表示对像素 $p$ 和 $q$ 取值不连续性的惩罚, 取值越接近则 $B_{(p, q)}$ 越大, 反之越小.

2. Graph Cuts and Computer Vision

无向图 $\mathcal{G}=<\mathcal{V, E}>$ 定义为一族顶点 $\mathcal{V}$ 和连接这些点的边 $\mathcal{E}$ . 每条边 $e\in\mathcal{E}$ 都被赋予非负的权重(损失) $w_e$ . 我们引入两个特殊的顶点称为端点(terminals), 他们和图中所有其他点相连, 但彼此不直接相连. 一个割(cut)是边集的一个子集 $C\in\mathcal{E}$ 使得图中的两个端点被分离开 $\mathcal{G}(C):=<\mathcal{V, E}\backslash C>$ . 在组合优化中我们一般把割的损失定义为边上损失的和

\[\lvert C\rvert := \sum_{c\in C}w_e.\]

图割法求解优化目标(最小割)的方法是使用最大流最小割定理, 即求解最小割等价于求解最大流. 另外, 有两个端点的图的最小割有更高效的(低阶)多项式时间算法求解.

3. Segmentation Technique

假设 $\mathcal{O}$ 和 $\mathcal{B}$ 表示已经被用户标记为”(目标)object”和”(背景)background”像素的集合, 那么有 $\mathcal{O}\in\mathcal{P}$ 和 $\mathcal{B}\in\mathcal{P}$ 并且 $\mathcal{O}\cap\mathcal{B}=\emptyset$ . 我们的目标是计算公式(2)满足硬约束

\[\begin{align} \forall p\in\mathcal{O},\qquad & A_p = \text{"obj"} \\ \forall p\in\mathcal{B},\qquad & A_p = \text{"backround"}. \end{align}\]

的全局最优解. 从图像构建图如下图所示.

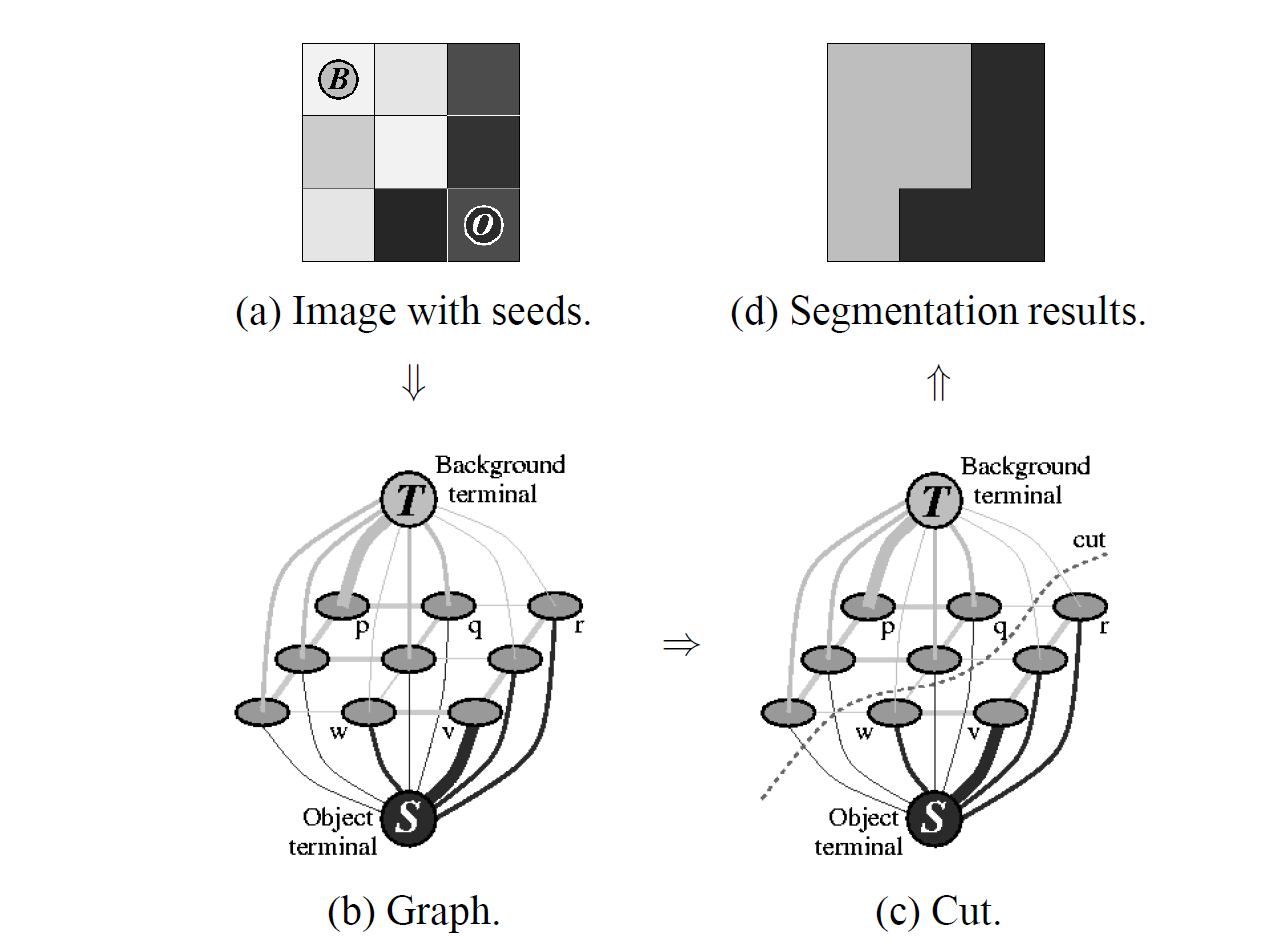
A simple 2D segmentation example for a 3x3 image.

3.1 Details

图 $\mathcal{G}=<\mathcal{V, E}>$ , 其中顶点包括图像中的像素点和两个端点(源点 $S$ 和汇点 $T$), 所以有

\[\mathcal{V} = \mathcal{P}\cup\{S, T\}.\]

边集包括两种类型的边: (1) n-links (neighborhood links) 和 t-links (terminal links). 每个像素点 $p$ 都关联了边 $(p, S)$ 和 $(p, T)$ . 集合 $\mathcal{N}$ 中的邻居像素 $(p, q)$ 都关联了一条 n-link. 所以有

\[\mathcal{E} = \mathcal{N}\bigcup_{p\in\mathcal{P}}\{(p, S), (p, T)\}.\]

为了清晰, 我们把不同类型边的权重列在下面的表格中

edge	weight(cost)	for
$$ (p, q) $$	$$ B_{(p, q)} $$	$$ (p, q)\in\mathcal{N} $$
$$ \{p, S\} $$	$$ \lambda\cdot R_p(\text{"bkg"}) $$	$$ p\in\mathcal{P},\;p\notin\mathcal{O}\cup\mathcal{B} $$
	$$ K $$	$$ p\in\mathcal{O} $$
	$$ 0 $$	$$ p\in\mathcal{B} $$
$$ \{p, T\} $$	$$ \lambda\cdot R_p(\text{"obj"}) $$	$$ p\in\mathcal{P}, \;p\notin\mathcal{O}\cup\mathcal{B} $$
	$$ 0 $$	$$ p\in\mathcal{O} $$
	$$ K $$	$$ p\in\mathcal{B} $$

其中

\[K = 1 + \max_{p\in\mathcal{P}}\sum_{q:(p, q)\in\mathcal{N}}B_{(p, q)}.\]

3.2 Min-Cut

我们想要的最小割 $C$ 应该满足以下条件:

在每个像素点 $p$ 上只有一条 t-link 属于 $C$
$(p, q)\in C$ 当且仅当 $p, q$ 连接到不同的端点
如果 $p\in\mathcal{O}$ , 则 $(p, T)\in C$
如果 $p\in\mathcal{B}$ , 则 $(p, S)\in C$

4. Examples

从用户标记的像素中提取直方图作为密度分布的先验 $Pr(I\lvert\mathcal{O})$ 和 $Pr(I\lvert\mathcal{B})$ . 那么区域惩罚可以写为

\[\begin{align} R_p(\text{"obj"})&=-\ln Pr(I_p\lvert\mathcal{O}) \\ R_p(\text{"bkg"})&=-\ln Pr(I_p\lvert\mathcal{B}). \end{align}\]

而边界惩罚使用 ad-hoc 函数

\[B_{\{p, q\}}\propto\exp\left(-\frac{(I_p-I_q)^2}{2\sigma^2}\right)\cdot\frac1{dist(p, q)}.\]

注意: 在 2D 图像中使用 8-neighborhood, 在 3D 图像中使用 26-neighborhood.

5. Appendix*

网络流问题: 给定一个网络图和两个端点(源点s和汇点t), 每条边有一定的容量, 计算从s到t的最大流量.

A. Maxflow Basic Algorithm

基础算法 - Ford Fulkerson 算法:

Inputs Given a Network $G=(V,E)$ with flow capacity $c$, a source node $s$, and a sink node $t$ .
Output Compute a flow f from $s$ to $t$ of maximum value
1. Residual graph $G_f(u, v)\leftarrow G(u, v)$ for all edges $(u, v)$ . $maxflow\leftarrow 0$ .
2. while there is a path $p$ from $s$ to $t$ in $G_f$ , such that $c_f(u, v)>0$ for all edges $(u, v)\in p$ :
  1. Find $c_f(p)=\min[c_f(u, v): (u, v)\in p]$
  2. Accumulate: $maxflow \leftarrow maxflow + c_f(p)$ .
  3. Update residual graph $G_f$ . For each edge $(u, v)\in p$ :
    1. $G_f(u, v)\leftarrow G_f(u, v)-c_f(p)$ (Send flow along the path)
    2. $G_f(v, u) \leftarrow G_f(v, u) + c_f(p)$ (The flow might be “returned” later)
3. Get edges of the min-cut (if need):
  1. Run BFS(breadth first search) from $s$ in $G_f$
  2. Traversed points construct $O$ and non-traversed points construct $B$ .
4. Return $maxflow$ and $O$ and $B$ (min-cut is the edges between $O$ and $B$ in $G_f$ ).

B. Maxflow for Energy Minimization

Title: An Experimental Comparison of Min-Cut/Max-Flow Algorithms for Energy Minimization in Vision

Author: Yuri Boykov, Vladimir Kolmogorov

改进算法: 维护两个不重叠的搜索树 $S$ 和 $T$, 它们的根分别是源 $s$ 和汇 $t$, 同时满足 $S$ 树的父节点到子节点的边流量不满(nonsaturated), $T$ 树的子节点到父节点流量不满. 不在树中的其他节点为”自由节点”. 树节点分为激活的(active)和抑制的(passive, 暂且叫成抑制的吧). 激活的节点可以继续扩展新的子节点(从相邻的自由节点中选择, 2D 为8相邻, 3D为26相邻), 抑制的节点没有相邻的自由节点可扩展.

如图所示:

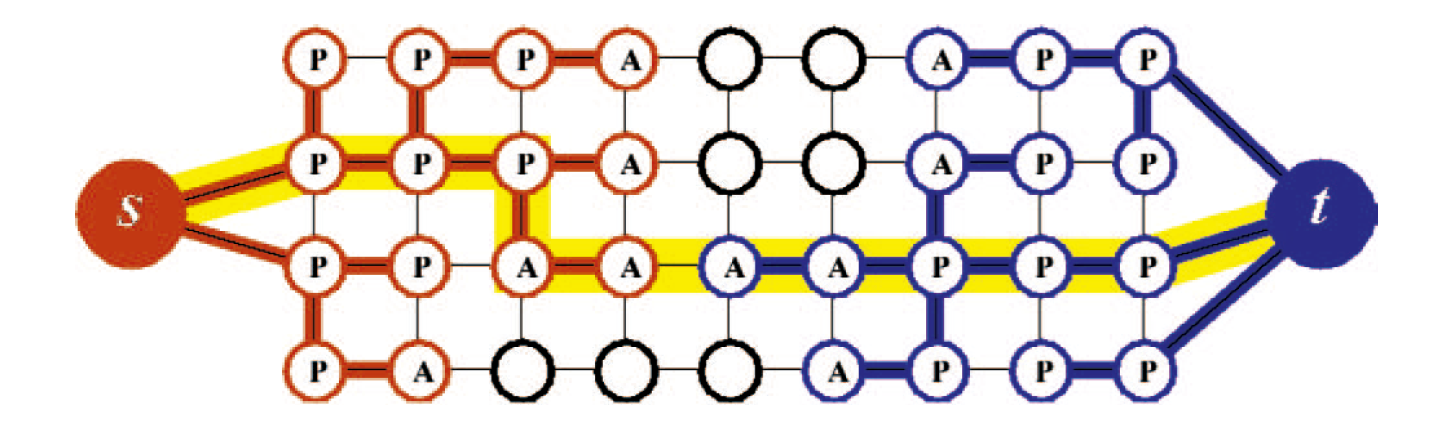
Example of the search tree S(read nodes) and T(blue nodes) at the end of the growth stage when a path(yellow line) from the source s to the sink t is found. Active and passive nodes are labeled by letters A and P, correspondingly. Free nodes appear in black.

算法流程:

“增长(growth)”阶段: 搜索树 $S$ 和 $T$ 增长, 直到两棵树”接触”到从而产生一条 $s\rightarrow t$ 路径.
- 为了简便, 记树从根到叶方向的边为正向边, 从叶到根方向的边为反向边
“增广(augmentation)”阶段: 增广上一步找到的路径, 搜索树均变为森林.
1. 寻找”瓶颈”容量 $\Delta$
2. 增广: (1) 更新残差图(residual graph): $S$ 树的正向边(根->叶)容量减少 $\Delta$, 反向边(叶->根)容量增加 $\Delta$; $T$ 树做相反的增减(对于流图来说是做了相同方向的增减). (2) 打断流图满容量的正向边, 并把该边的头节点加入孤儿(orphan)列表.
  - 注意: $S$ 树的正向边是流图“从源到汇”的正向边, $T$ 树的反向边是流图“从源到汇”的正向边.
“应用(adoption)”阶段: restore树 $S$ 和 $T$ .
- 依次处理孤儿列表中的节点 $p$
  1. 为 $p$ 寻找一个新的父节点 $q$ , 父节点要满足三个条件: (1)边 $(p, q)$ 容量不满, (2)父子来自于同一棵树(孤儿则考虑其原来的父亲来自于哪棵树), (3)父节点的”origin”为 $s$ 或 $t$ .
  2. 如果找到了多个可行的父节点, 则选择离 $p$ 最近的那个
  3. 如果找到了新的父节点 $q$, 则把 $q$ 设为 $p$ 新的父节点; 如果没找到, 则把 $p$ 恢复为自由节点, 并做以下操作
    - 扫描 $p$ 的所有同一棵树上的邻居 $q$, 如果边 $(q, p)$ 容量不满, 则把 $q$ 设为激活节点; 如果 $q$ 的父节点是 $p$, 则把 $q$ 添加到孤儿列表.
    - 把 $p$ 从激活节点列表中移除.
以上三步循环直到没有新的激活节点.

技术报告和实现源码(第三方): Code

示例图片:

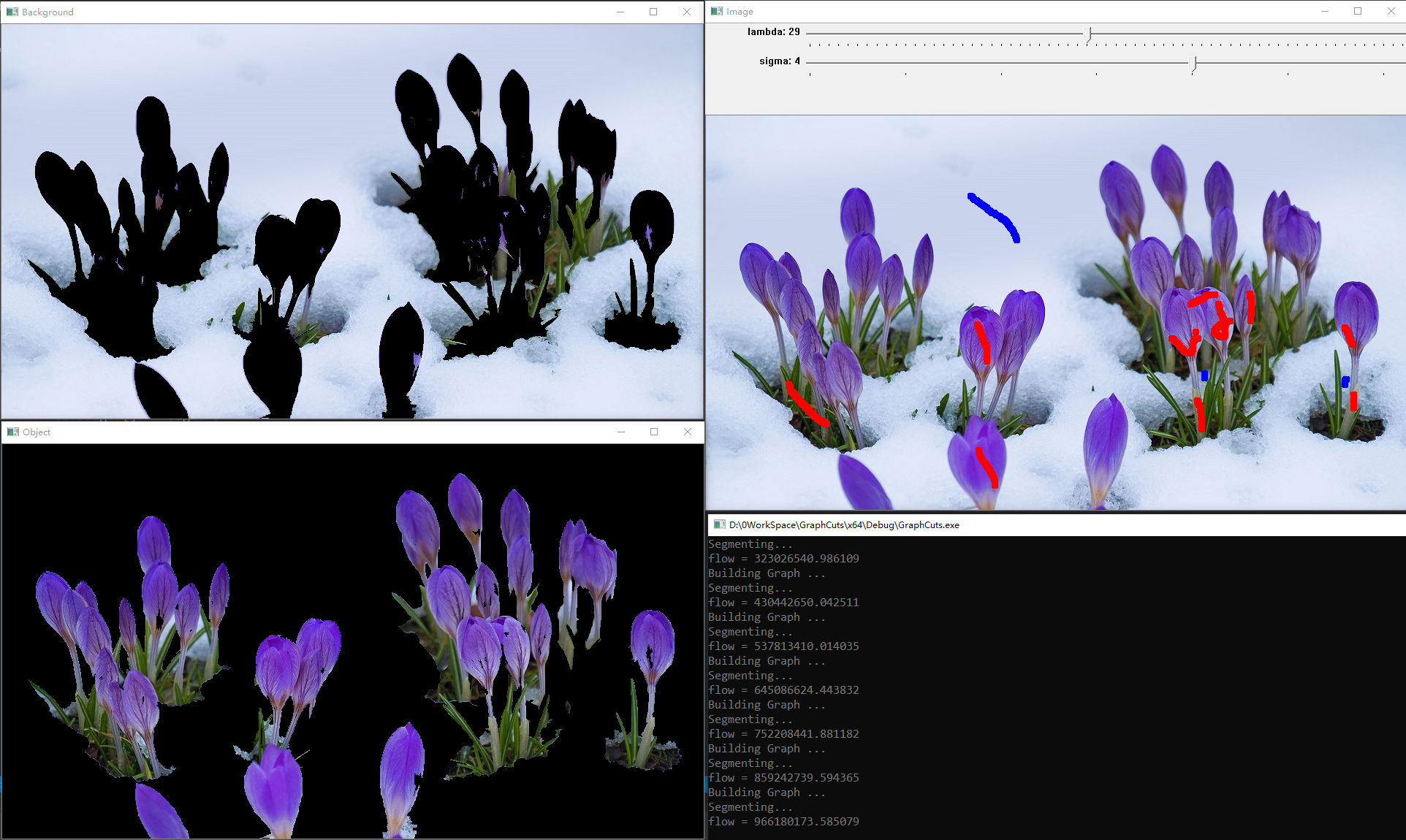
Graph-Cuts 示例

C. GrabCut

Title: “GrabCut” – Interactive Foreground Extraction using Iterated Graph Cuts

Author: Carsten Rother, Vladimir Kolmogorov, Andrew Blake

GrabCut 是 OpenCV 中标准的交互式图割算法.

本文基于文献[1], 为了简化交互负担, 允许用户开始只需要用矩形框框出目标物体即可. 在某些图像上可以达到和用户使用画笔涂抹一样甚至更好的效果. 此外, GrabCut 还允许用户在对风格结果不满意时进一步使用 Graph Cuts 的交互方式补全. 同时 GrabCut 支持彩色图像的分割. GrabCut 的分割例子如图所示.

GrabCut 示例

文献[1]中的能量函数中region项使用用户涂抹区域的密度分布的对数建模, 而本文 GrabCut 则使用两个有 $K$ 个成分的高斯混合模型(Gaussian Mixture Model, GMM)分别对前景和背景进行建模. 为了方便优化, 增加一个向量 $\mathbf{k}=(k_1, \cdots, k_n, \cdots, k_N)$, 其中 $k_n\in[1, \dots, K]$ 是赋予每一个像素的一个 GMM 成分. 从而能量函数 $E(A)$ 中的 region 项 $R(A)$ 变为

\[R(\alpha, \mathbf{k}, \theta, \mathbf{z}) = \sum_n D(\alpha_n, k_n, \theta, z_n),\]

其中 $D$ 表示 GMM 分布函数的对数, 此处不再展开. $\alpha$ 表示不透明度 (取值于0和1), 决定了一个像素属于前景还是背景.

算法流程:

初始化
- 用户绘制的矩形框 $T_B$, 前景集合设为 $T_F=\emptyset$, 背景集合 $T_U=\overline{T_B}$. 对于 $n\in T_B$, 初始化 $\alpha_n=0$, 其他为 $1$.
- 前景和背景的 GMMs 分别根据 $\alpha_n$ 取值初始化.
迭代优化
1. Assign GMM components to pixels: for each $n$ in $T_U$,
\[k_n:=\arg\min_{k_n}D_n(\alpha_n, k_n, \theta, z_n).\]
1. Learn GMM parameters from data $\mathbf{z}$:
\[\theta := \arg\min_{\theta}U(\alpha, \mathbf{k}, \theta, \mathbf{z}).\]
1. Estimate segmentation: use min cut to solve:
\[\min_{\alpha_n:n\in T_U}\min_{\mathbf{k}}\mathbf{E}(\alpha, \mathbf{k}, \theta, \mathbf{z}).\]
1. Repeat from step 1, until convergence.
2. Apply border matting.

(未完待续…)

6. References

Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Object in N-D Images
Yuri Y. Boykov, Marie-Pierre Jolly.
[link]. In ICCV, 2001.
An Experimental Comparison of Min-Cut/Max-Flow Algorithms for Energy Minimization in Vision
Yuri Boykov, Vladimir Kolmogorov.
[link]. In TPAMI 2004.
“GrabCut” – Interactive Foreground Extraction using Iterated Graph Cuts
Carsten Rother, Vladimir Kolmogorov, Andrew Blake
[link]. ACM TOG, 2004