文章标题: Optimal Graph Search Based Segmentation of Airway Tree Double Surfaces Across Bifurcations
作者: Xiaomin Liu, Danny Z. Chen, Merryn H. Tawhai, Xiaodong Wu, Eric A. Hoffman, Milan Sonka
介绍
本文是在文章Optimal Surface Segmentation in Volumetric Images — A graph-Theoretic Approach(下称前文)的基础上专门针对支气管的分割而设计的图搜索方法, 本文的核心算法与前文基本一致, 所以下面不再重述, 我们把关注点放在针对支气管的设计上, 同时我们延续前文中使用的术语.
基于图搜索的分割
前文主要是通过把图像分割问题转化为寻找最小损失闭集的问题, 本文针对气管的分割方法主要分为以下四步:
- 原始图像的预分割及其曲面的网格表示,
- 图像的重采样,
- 图的构建,
- 图的搜索.
预分割
直接用现成的软件做预分割, 而且只能分出气管内壁, 对于较小的支气管无能为力. 内壁分割出来内壁通过marching cube算法表示成三角网.
基于中轴的图像重采样
由于我们分割的是树状的气管和支气管, 所以不能再按照前文的想法基于类”地形图”的方法来构建图, 而是要按照前文提到的柱形的方法来构建, 前文中的 \((x, y)\) –列也不再使用, 而是变成了以气管中轴线为参照的轴向体素列. 如图1(a)所示.
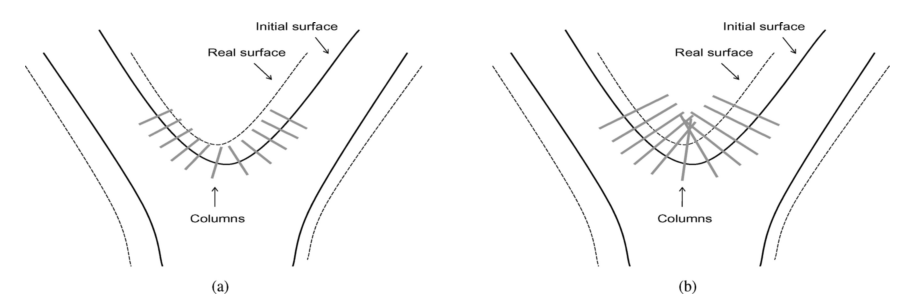
图1: 以气管中轴线为参照的轴向体素列和可能存在的问题
使用线性插值进行重采样. 这里要特别避免两种”坏”的情况:
- 体素列的长度太短, 以至于图无法抓取到曲面足够的信息;
- 体素列的长度太长, 以至于与其他的体素列相交, 如图1(b)所示. 显然气管分叉的角度太小和较为末端的支气管处必然会发生这种情况.
由于前文中讨论的是类”地形图”的曲面, 所以可以用统一的列长, 而支气管非常复杂, 无法使用统一的列长, 如图2所示. 为了解决上面的问题, 我们使用了如下的方法:
- 使用预分割表面的中轴线来帮助避免体素列的相交;
- 对预分割表面做膨胀操作, 保证不干扰的体素列足够长从而能够包含最优位置, 同时消除尖角的情况.
预分割表面的中轴线是一系列点的集合, 该集合中的每一个点都一定与表面上至少两个点距离最近. 中轴线算法:
- 记预分割表面的网格点的集合为 \(S\) , 然后计算 \(S\) 的泰森多边形(Voronoi diagram, VD)和对偶的德劳内三角剖分(Delaunay triangulation)D;
- 对每个顶点均求一对 \(v_{p_1}\) 和 \(v_{p_2}\) 分别作为内中轴线和外中轴线, 这两点选为最大的德劳内球的球心(德劳内四面体的外切球球心);
- 选择球心是选择点 \(p\) 的 \(k\) 个最近邻中最大的值;
- 体素列的长度由体素到中轴线的距离决定.
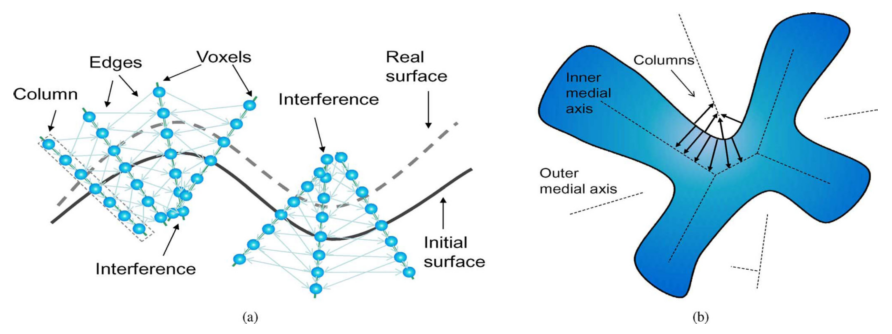
图2: 图像重采样和图的构建. (a)不合适的体素列长导致的冲突. (b) 使用中轴线确定体素列长避免冲突
图构建
图的构建方法与前文一样基于光滑性约束, 列分离性约束和面分离约束. 值得注意的是这里每个点与两个体素列相关联, 一个向内用于检测内壁, 一个向外用于检测外壁. 具体构建方法参考前文.
损失函数
损失函数定义如下:
\[\text{Cost}_{\text{outer}}(v) = \omega\cdot I_t(v)*M_{Sobel_1} = (1-\omega)\cdot I_t(v)*M_{Marr},\] \[\text{Cost}_{\text{inner}}(v) = \omega\cdot I_t(v)*M_{Sobel_2} = (1-\omega)\cdot I_t(v)*M_{Marr}.\]其中 \(M_{Sobel_i}\) 表示Sobel算子, \(M_{Marr}\) 表示Marr算子, 且均为二维滤波器, 如图3所示.
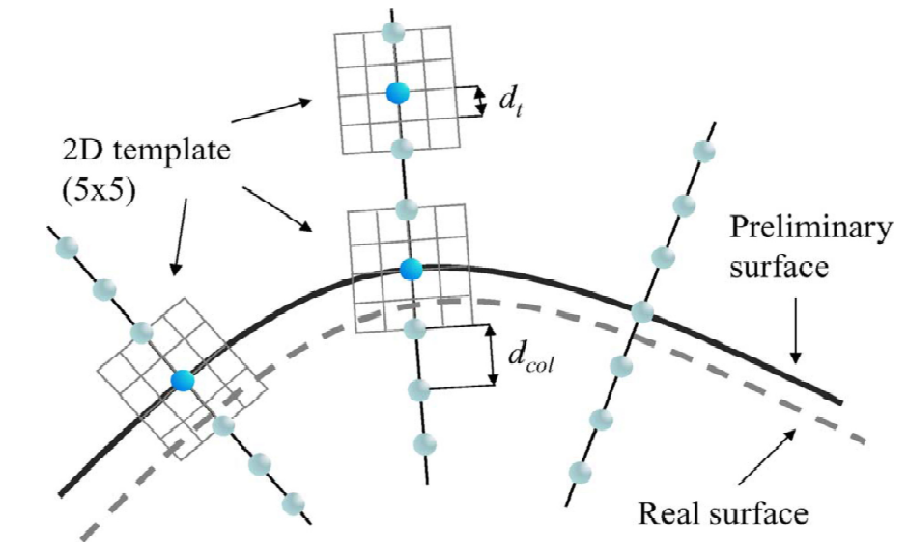
图3: 损失函数